坐标变换与矢量旋转

在多体动力学建模中，通常会建立多个坐标系，其中会涉及大量的坐标变换。坐标变换是由于参考系的姿态差异导致，因此与旋转存在联系。本文旨在讨论坐标变换与旋转之间的数学关系与区别，并推导坐标变换矩阵的动力学特性。

矢量的坐标表示

有大小和方向的物理量称为矢量（Vector），通常用带箭头的符号表示，如 $\vec{r}$。为了定量描述与计算，需要选定基矢构成参考系，利用矢量合成原理进行表述。如下图所示，参考系 $\mathscr{A} = \{O,\,\vec{a}_1,\,\vec{a}_2 \}$ 以 $O$ 为原点，$\vec{a}_1$ 和 $\vec{a}_2$ 为基矢。任意矢量 $\vec{r}$ 可以写作

$$ \vec{r} = r_1^a \vec{a}_1 + r_2^a \vec{a}_2 = \begin{bmatrix} \vec{a}_1 & \vec{a}_2 \end{bmatrix} \begin{bmatrix} r_1^a \\ r_2^a \end{bmatrix} = \vec{A} \bm{r}^a $$

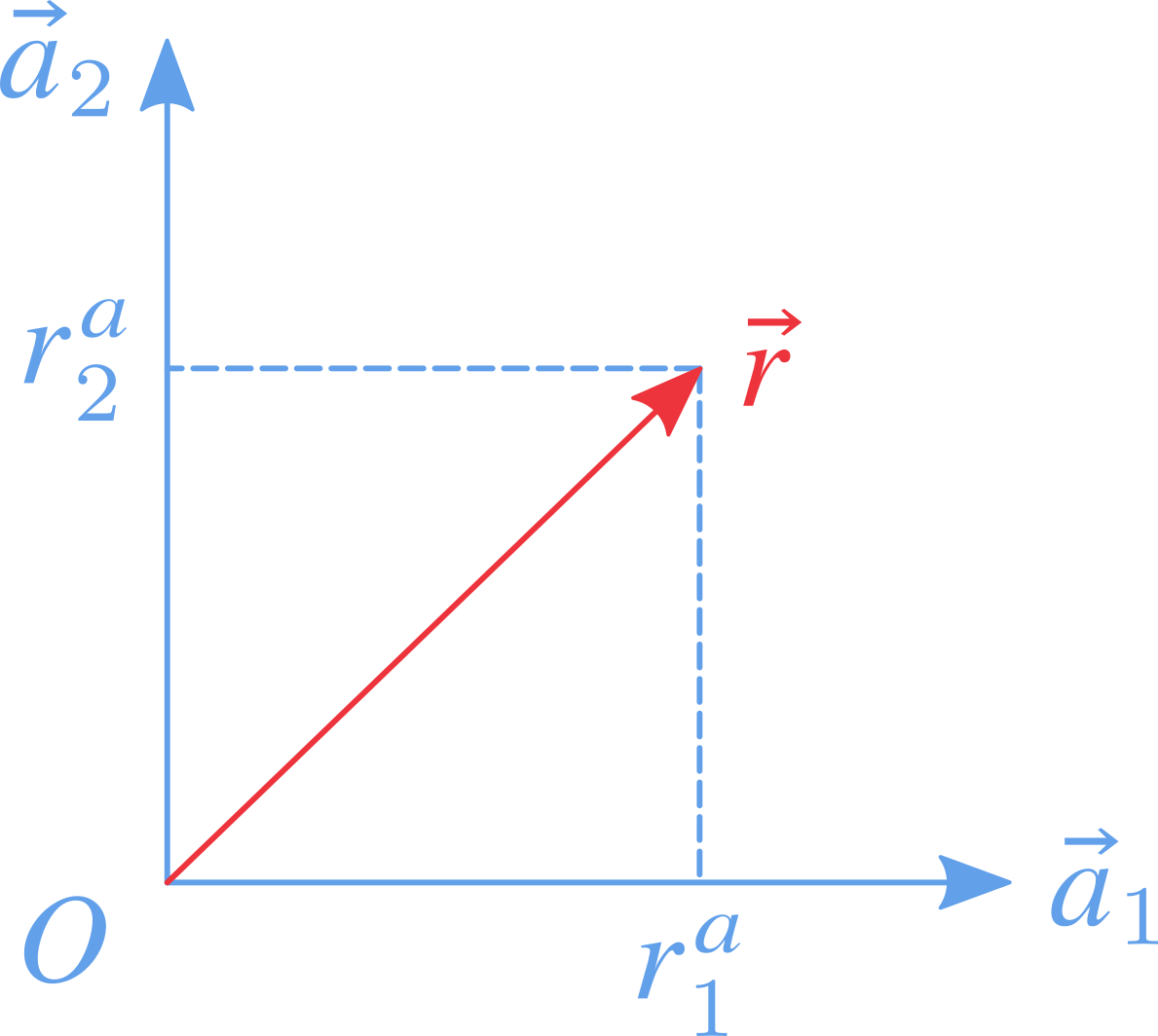
这里我们使用带箭头的大写字母表示参考系基矢构成的行向量，即 $\vec{A} = [\vec{a}_1, \vec{a}_2]$；选定基矢后，基矢的组合系数构成列向量，为矢量的坐标（Coordinate），用加粗的字母表示，并将参考系标记在上标的位置，本例中为 $\bm{r}^a= [r_1^a, r_2^a]^\mathrm{T}$。在此记号下，我们可以使用矩阵的计算方法将适量表示为基矢与坐标的组合，即上式最后的等号。在后文的推导中，我们将使用更一般的三维形式，而为了方便理解，示意图保持为二维形式。

如无特别说明，参考系的基矢通常选为单位正交基，其点积满足

$$ \vec{A}^\mathrm{T} \cdot \vec{A} = \begin{bmatrix} \vec{a}_1 \\ \vec{a}_2 \\ \vec{a}_3 \end{bmatrix} \cdot \begin{bmatrix} \vec{a}_1 & \vec{a}_2 & \vec{a}_3 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} = I_{3 \times 3} $$

由此我们可以获知坐标的计算方法：

$$ \bm{r}^a = I_{3 \times 3} \bm{r}^a = \left( \vec{A}^\mathrm{T} \cdot \vec{A} \right) \bm{r}^a = \vec{A}^\mathrm{T} \cdot \left( \vec{A} \bm{r}^a \right) = \vec{A}^\mathrm{T} \cdot \vec{r} = \begin{bmatrix} \vec{a}_1 \cdot \vec{r} \\ \vec{a}_2 \cdot \vec{r} \\ \vec{a}_3 \cdot \vec{r} \\ \end{bmatrix} $$

上式指出，为了获取矢量在给定参考系下的坐标，只需计算矢量与参考各基矢之间的点积即可，即：坐标是矢量在基矢方向的投影。

坐标变换

选取的参考系不同，相同矢量的坐标不同。参考系之间的平移可以简单地通过矢量加法实现，因此这里的坐标变换重点关注参考系之间的转动，设它们的原点重合（因此后文直接用基矢表示各参考系），如下图所示。

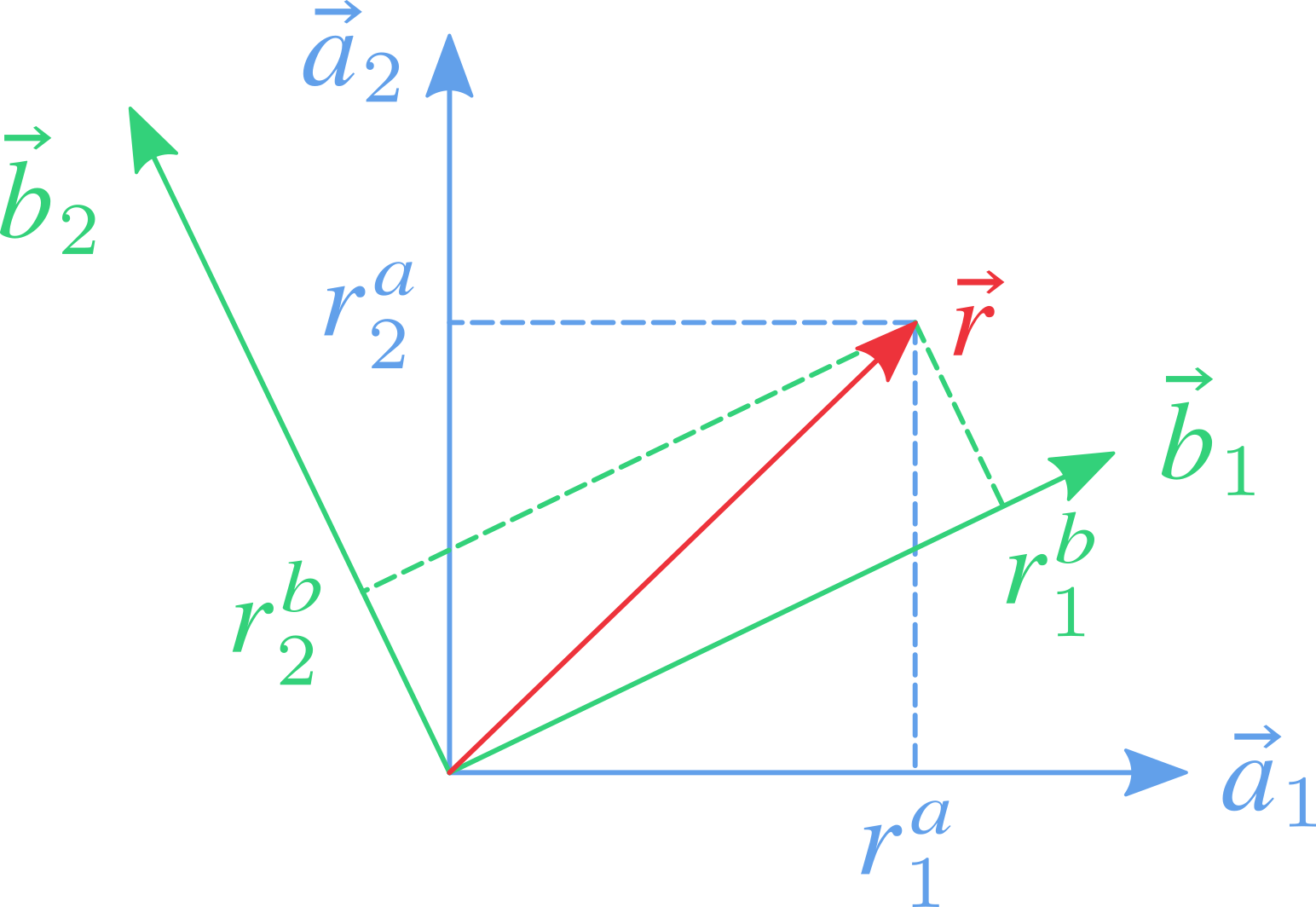
矢量 $\vec{r}$ 可以在两个参考系中分别表述为

$$ \vec{r} = \vec{A} \bm{r}^a = \vec{B} \bm{r}^b $$

考察坐标之间的关系，不难得到

$$ \bm{r}^b = \vec{B} \cdot \vec{r} = \vec{B}^\mathrm{T} \cdot \left( \vec{A} \bm{r}^a \right) = \left( \vec{B}^\mathrm{T} \cdot \vec{A} \right) \bm{r}^a = R_a^b \bm{r}^a $$

其中 $R_a^b$ 为坐标变换矩阵，其表示从参考系 $\vec{A}$ 到参考系 $\vec{B}$ 的坐标变换（从下往上读）。从上式的两端可以发现，在这种表述方式下，角标形式上具有“相互抵消”的性质，即：如果左侧变量的下标与右侧变量的上标相同，则抵消两个角标并根据左侧变量的上标替换掉右侧变量的上标。后面讨论的连续坐标变换能够充分体现这种特性。

坐标变换矩阵 $R_a^b$ 具体展开为

$$ \begin{aligned} R_a^b &= \begin{bmatrix} \vec{B}^\mathrm{T} \cdot \vec{a}_1 & \vec{B}^\mathrm{T} \cdot \vec{a}_2 & \vec{B}^\mathrm{T} \cdot \vec{a}_3 \end{bmatrix} = \begin{bmatrix} \bm{a}_1^b & \bm{a}_2^b & \bm{a}_2^b \end{bmatrix} \\ &= \begin{bmatrix} \vec{b}_1 \cdot \vec{A} \\ \vec{b}_2 \cdot \vec{A} \\ \vec{b}_3 \cdot \vec{A} \\ \end{bmatrix} = \begin{bmatrix} \left(\bm{b}_1^a\right)^\mathrm{T} \\ \left(\bm{b}_2^a\right)^\mathrm{T} \\ \left(\bm{b}_3^a\right)^\mathrm{T} \end{bmatrix} \end{aligned} $$

上式中，第一行说明坐标变换矩阵可以按列解释：每一列分别由参考系 $\vec{A}$ 的各基矢在参考系 $\vec{B}$ 中的坐标组成；第二行说明该矩阵也可以按行解释：每一行为参考系 $\vec{B}$ 的各基矢在参考系 $\vec{A}$ 中的坐标（的转制）组成 。我们通常倾向于按列解释，这样可以保持上标的一致性。由于单位向量的点积等于夹角的余弦，因此坐标变换矩阵也称作方向余弦矩阵（DCM, Direction Cosine Matrix）。

考虑矢量 $\vec{r}$ 按照 $\vec{A} \rightarrow \vec{B}_1 \rightarrow \vec{B}_2 \rightarrow \cdots \rightarrow \vec{B}_n$ 的顺序进行 $n$ 次坐标变换，有

$$ \bm{r}^{b_n} = R_{b_{n-1}}^{b_n} \bm{r}^{b_{n-1}} = R_{b_{n-1}}^b \left( R_{b_{n-2}}^{b_{n-1}}\bm{r}^{b_{n-2}} \right) = \cdots = \left( R_{b_{n-1}}^b R_{b_{n-2}}^{b_{n-1}} \cdots R_a^{b_{1}} \right) \bm{r}^a $$

即

$$ R_a^{b_n} = R_{b_{n-1}}^{b_n} R_{b_{n-2}}^{b_{n-1}} \cdots R_a^{b_{1}} $$

说明连续坐标变换矩阵为各坐标变换矩阵按顺序左乘的结果。

最后，我们重新将坐标变换矩阵代回到矢量表达式中，得

$$ \vec{r} = \vec{A} \bm{r}^a = \vec{B} \bm{r}^b = \vec{B} R_a^b \bm{r}^a \quad \Rightarrow \quad \vec{A} = \vec{B} R_a^b $$

最后的等号暗示了坐标系之间的关系，将在后文矢量旋转那里做进一步说明。利用基矢的正交性，有

$$ I_{3 \times 3} = \vec{A}^\mathrm{T} \cdot \vec{A} = \left( \vec{B} R_a^b \right)^\mathrm{T} \cdot \left( \vec{B} R_a^b \right) = \left(R_a^b \right)^\mathrm{T} \left(\vec{B}^\mathrm{T} \cdot \vec{B}\right) R_a^b = \left(R_a^b \right)^\mathrm{T} R_a^b $$

这说明坐标变换矩阵 $R_a^b$ 为正交矩阵，即 $\left(R_a^b \right)^{-1} = \left(R_a^b \right)^\mathrm{T}$。我们可以令 $R_b^a = \left(R_a^b \right)^{-1}$，则 $R_a^b R_b^a = R_b^a R_a^b = I$ 意味着来回变换之后坐标保持不变（这里可以再次看到角标之间的“抵消”性质）。

矢量旋转

将目光限定在参考系 $\vec{A}$ 中，现在将矢量 $\vec{r}_1$ 进行一定的旋转，得到 $\vec{r}_2$ ，如何得到它们坐标 $\bm{r}_1^a$ 和 $\bm{r}_2^a$ 之间的关系？

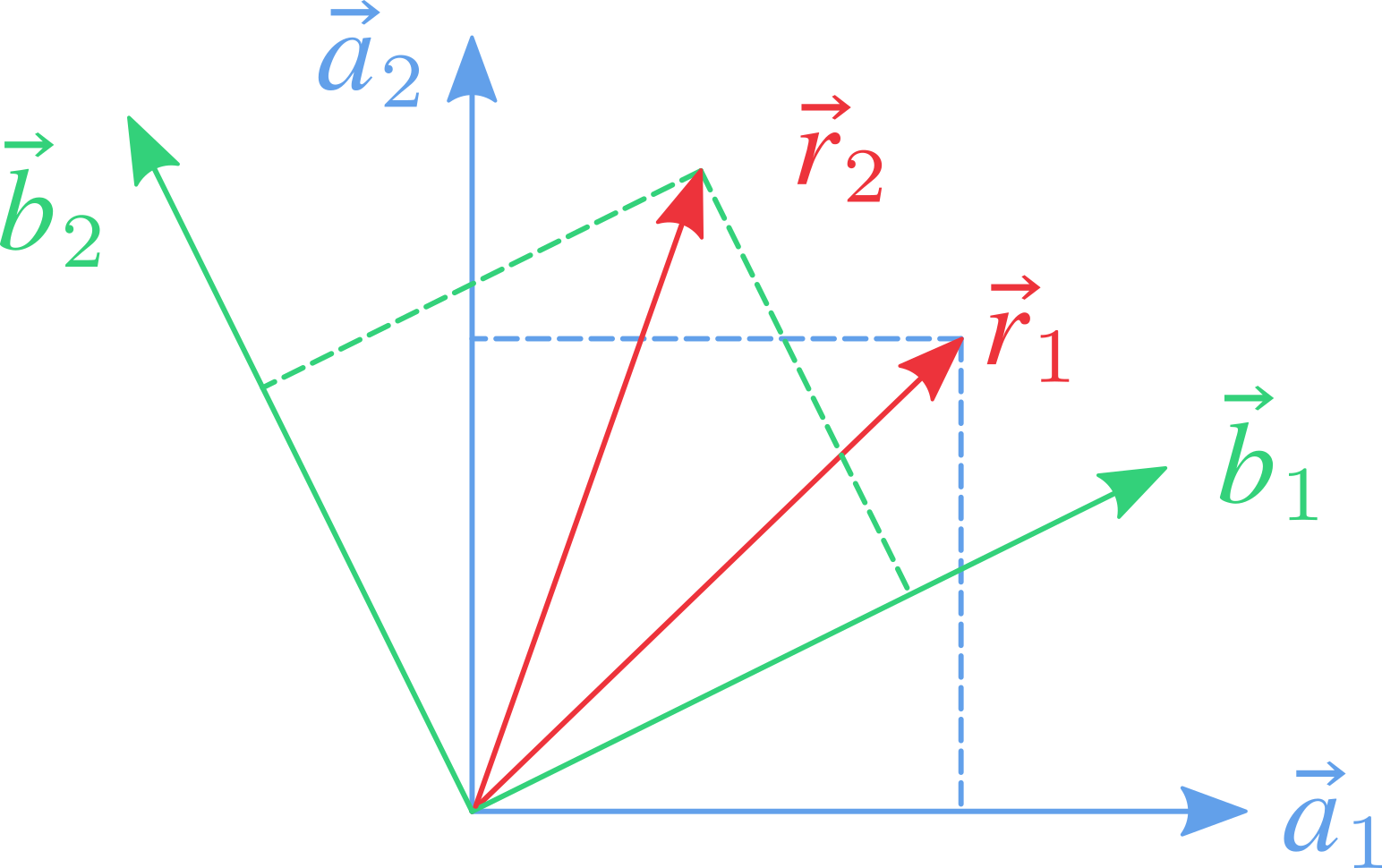
考虑 $\vec{r}_1$ 连同参考系（的基矢） $\vec{A}$ 一起旋转，当 $\vec{r}_1$ 转到 $\vec{r}_2$ 的位置时 $\vec{A}$ 相应地变成 $\vec{B}$。由于是一起旋转，相对关系保持不变，即 $\vec{r}_2$ 在 $\vec{B}$ 的坐标等于 $\vec{r}_1$ 在 $\vec{A}$ 的坐标，即 $\bm{r}_2^b = \bm{r}_1^a$，考虑到坐标变换有 $\bm{r}_2^a = R_b^a \bm{r}_2^b$，可以得到

$$ \bm{r}_2^a = R_b^a \bm{r}_1^a $$

这就说明，坐标变换矩阵同时具有旋转的含义，也可称之为旋转矩阵， $R_b^a$ 表示从参考系 $\vec{A}$ 到参考系 $\vec{B}$ 的旋转（从上往下读，注意这里交换了角标）。

在对实际物体旋转的描述中，通常使用本体坐标系之间的关系。在上文我们实际上已经得到了 $\vec{A} = \vec{B} R_a^b$，这同样可以“从上往下”地解读为 $\vec{B}$ 旋转到 $\vec{A}$。

考虑参考系 $\vec{r}$ 按照 $\vec{A} \rightarrow \vec{B}_1 \rightarrow \vec{B}_2 \rightarrow \cdots \rightarrow \vec{B}_n$ 的顺序进行 $n$ 次旋转，有

$$ \vec{B}_n = \vec{B}_{n-1} R_{b_{n}}^{b_{n-1}} = \vec{B}_{n-2} R_{b_{n-1}}^{b_{n-2}} R_{b_{n}}^{b_{n-1}} = \cdots = \vec{A} R_{b_1}^a \cdots R_{b_{n-1}}^{b_{n-2}} R_{b_{n}}^{b_{n-1}} $$

即 $\vec{A}$ 到 $\vec{B}_n$ 的连续旋转结果为

$$ R_{b_n}^a = R_{b_1}^a R_{b_2}^{b_1} \cdots R_{b_{n}}^{b_{n-1}} $$

最终的旋转矩阵 $R_b^a$ 为各次旋转矩阵按顺序右乘的结果。

转动的描述

最后我们来看一下坐标变换矩阵（或者说转动矩阵）的运动学特性。首先如下图所示，假设参考系 $\vec{B}$ （通常为刚体的本体参考系）的角速度为 $\bm{\omega}_b^b = [\omega_1,\omega_2,\omega_3]^\mathrm{T}$（注意角速度都是在本体坐标系下建立的，各分量省略了上标），以基矢 $\vec{b}_1$ 为例，在 $\mathrm{d}t$ 时间内其变化量为

$$ \mathrm{d}\vec{b}_1 = (\omega_3 \mathrm{d} t) \vec{b}_2 -(\omega_2 \mathrm{d}t)\vec{b}_3 + \quad \Rightarrow \quad \dot{\vec{b}}_1 = \omega_3 \vec{b}_2 -\omega_2 \vec{b}_3 $$

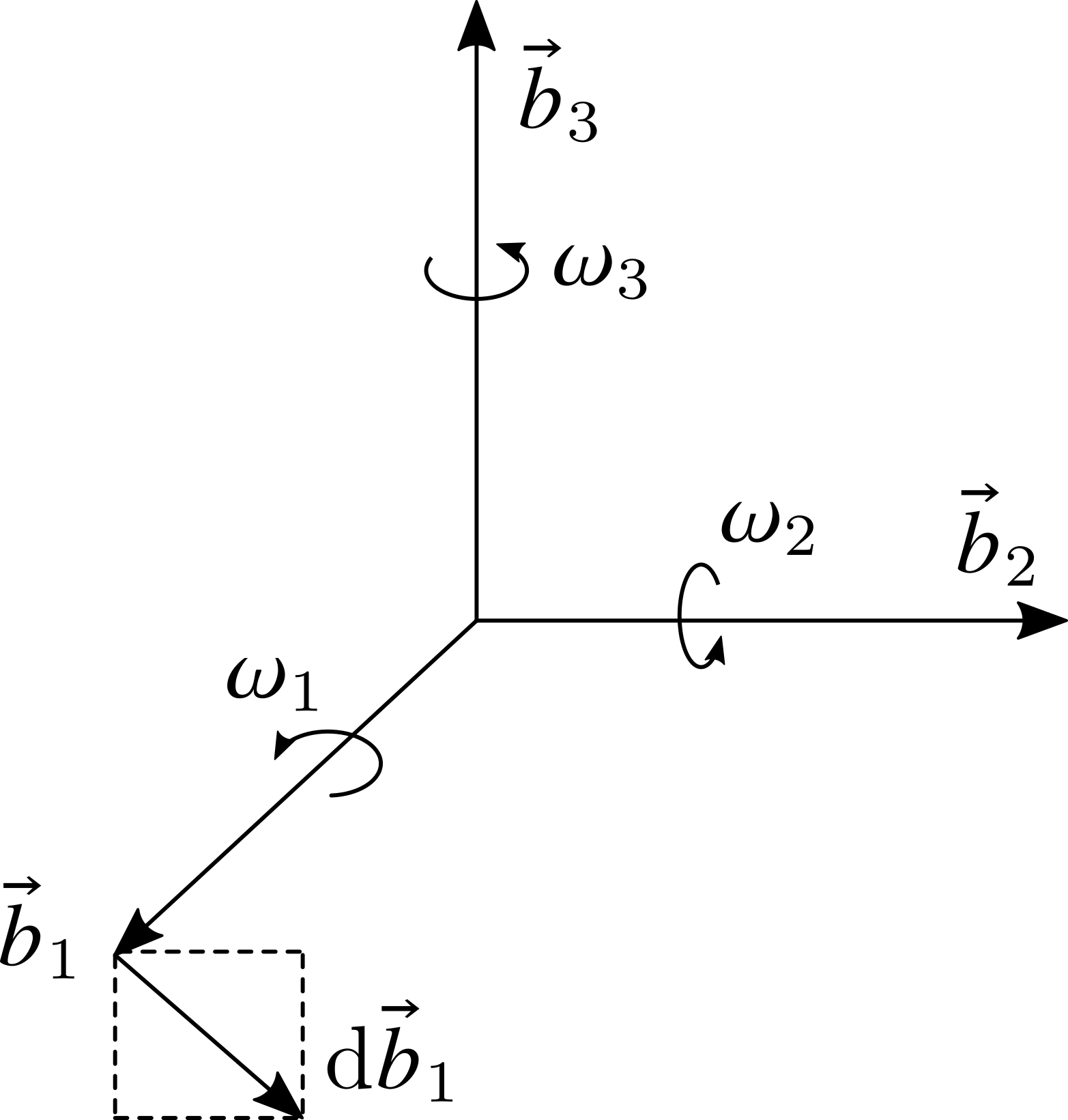
类似地，将三个基矢的导数整理为

$$ \begin{aligned} \dot{\vec{B}} &= \begin{bmatrix} \omega_3 \vec{b}_2 -\omega_2 \vec{b}_3 & -\omega_3 \vec{b}_1 + \omega_1 \vec{b}_3 & \omega_2 \vec{b}_1 - \omega_1 \vec{b}_2 \end{bmatrix} \\ &= \begin{bmatrix} \vec{b}_1 & \vec{b}_2 & \vec{b}_3 \end{bmatrix} \begin{bmatrix} 0 & -\omega_3 & \omega_2 \\ \omega_3 & 0 & -\omega_1 \\ -\omega_2 & \omega_1 & 0 \end{bmatrix} \\ &= \vec{B} \bm{\omega}_b^b \times \end{aligned} $$

我们将上式最后的 $3 \times 3$ 矩阵记做 $\bm{\omega}_b^b \times$，这样的表述与矢量的叉乘一致，且 $(\bm{\omega}_b^b \times)^\mathrm{T} = -\bm{\omega}_b^b \times$ 为反对称矩阵。最后，我们考察任意参考系 $\vec{A}$ 向本体系 $\vec{B}$ 的转动矩阵 $R_b^a$ 的导数，得

$$ \begin{aligned} \dot{R}_b^a &= \frac{\mathrm{d}}{\mathrm{d}t} \left( \vec{A}^\mathrm{T} \cdot \vec{B} \right) \\ &= \dot{\vec{A}}{}^\mathrm{T} \cdot \vec{B} + \vec{A}^\mathrm{T} \cdot \dot{\vec{B}} \\ &= (\bm{\omega}_a^a \times)^\mathrm{T} \vec{A}^\mathrm{T} \cdot \vec{B} + \vec{A}^\mathrm{T} \cdot \vec{B} (\bm{\omega}_b^b \times) \\ &= -(\bm{\omega}_a^a \times) R_b^a + R_b^a \bm{\omega}_b^b \times \\ &= -R_b^a (\bm{\omega}_a^b \times) + R_b^a \bm{\omega}_b^b \times \\ &= R_b^a \bm{\omega}_{ab}^b \times \end{aligned} $$

式中 $\bm{\omega}_{ab}^b = \bm{\omega}_b^b - \bm{\omega}_a^b$ 表示参考系之间的相对角速度在 $\vec{B}$ 参考系下的坐标。推导的倒数第二行使用了如下等式

$$ \bm{\omega}_a^b \times = \left( R_a^b \bm{\omega}_a^a \right) \times = R_a^b (\bm{\omega}_a^a \times) R_b^a $$

该等式的简单证明可以从角速度叉乘 $\vec{\omega}_a \times \vec{\omega}_b$ 在两个参考系下的表达获得：

$$ \left\{\begin{aligned} \vec{\omega}_a \times \vec{\omega}_b &= \vec{A} \bm{\omega}_a^a \times \bm{\omega}_b^a = \vec{A} (\bm{\omega}_a^a \times) R_b^a \bm{\omega}_b^b \\ \vec{\omega}_a \times \vec{\omega}_b &= \vec{B} \bm{\omega}_a^b \times \bm{\omega}_b^b =\vec{A}R_b^a \bm{\omega}_a^b \times \bm{\omega}_b^b \end{aligned}\right. \\ \Downarrow \\ (\bm{\omega}_a^a \times) R_b^a = R_b^a \bm{\omega}_a^b \times \\ \Downarrow \\ \bm{\omega}_a^b \times = \left( R_a^b \bm{\omega}_a^a \right) \times = R_a^b (\bm{\omega}_a^a \times) R_b^a $$

参考文献

1. E. Canuto, C. Novara, D. Carlucci, C.P. Montenegro, L. Massotti, Spacecraft Dynamics and Control: The Embedded Model Control Approach, Butterworth-Heinemann, 2018.