数据的强制类型转换及其应用

大春雨收录于类别优雅的算法

2022-09-03 2023-06-29 约 1571 字预计阅读 4 分钟

之前看到过一种快速求解平方根倒数的程序，里面包含了强制类型转换和一个神奇的常数，让人摸不着头脑。最近有兴趣了解了这个算法的细节，不禁叹为观止，以此文作为学习记录。

浮点数与整数的储存

IEEE 754 给出了浮点数的储存规范，其基本结构如下图所示（中括号内的的选项分别代表单精度数和双精度数）：

符号位（S, Sign）：占 $1$ 位，为 $0$ 时表示正数，为 $1$ 时表示负数；
指数位（E, Exponent）：表示 $2$ 的指数，可占据 $\mu_E = [8,11]$ 位；
小数位（M, Mantissa）：科学计数法中的小数部位，可占据 $\mu_M = [23, 52]$ 位。

为了能够更精细地表示小数，指数位应当覆盖负数。为此，指数部分应当扣除偏移：

$$ E_0 = 2^{\mu_E - 1} - 1 = \left[ 127,\, 1023 \right] $$

记

$$ M_0 = 2^{\mu_M} = \left[ 2^{23},\, 2^{52} \right] $$

则小数部分的分辨率为 $M_0^{-1}$，浮点数 $x$ 表示为

$$ x = (-1)^S 2^{E-E_0} \left( 1 + \frac{M}{M_0} \right) $$

式中 $S$、$E$ 和 $M$ 分别表示符号位、指数位和小数位直接按二进制读取的整数。为了更好地区分数据类型，采用大写字母表示整数、小写字母表示实数。

对数计算与强制类型转换

为了计算对数，我们将讨论范围局限为正实数，即假设符号位 $S=0$。于是有

$$ \log_2 x = \log_2 \left( 2^{E-E_0} \left( 1 + \frac{M}{M_0} \right) \right) = E-E_0 + \log_2 \left( 1 + \frac{M}{M_0}\right) \\ $$

考虑到 $\frac{M}{M_0}\in [0,1)$，在该区间内，对数函数可以取线性近似 $\log_2(1+t) \approx t + k$，例如取 $k=0.045$ 时，两者的对比如下图所示。

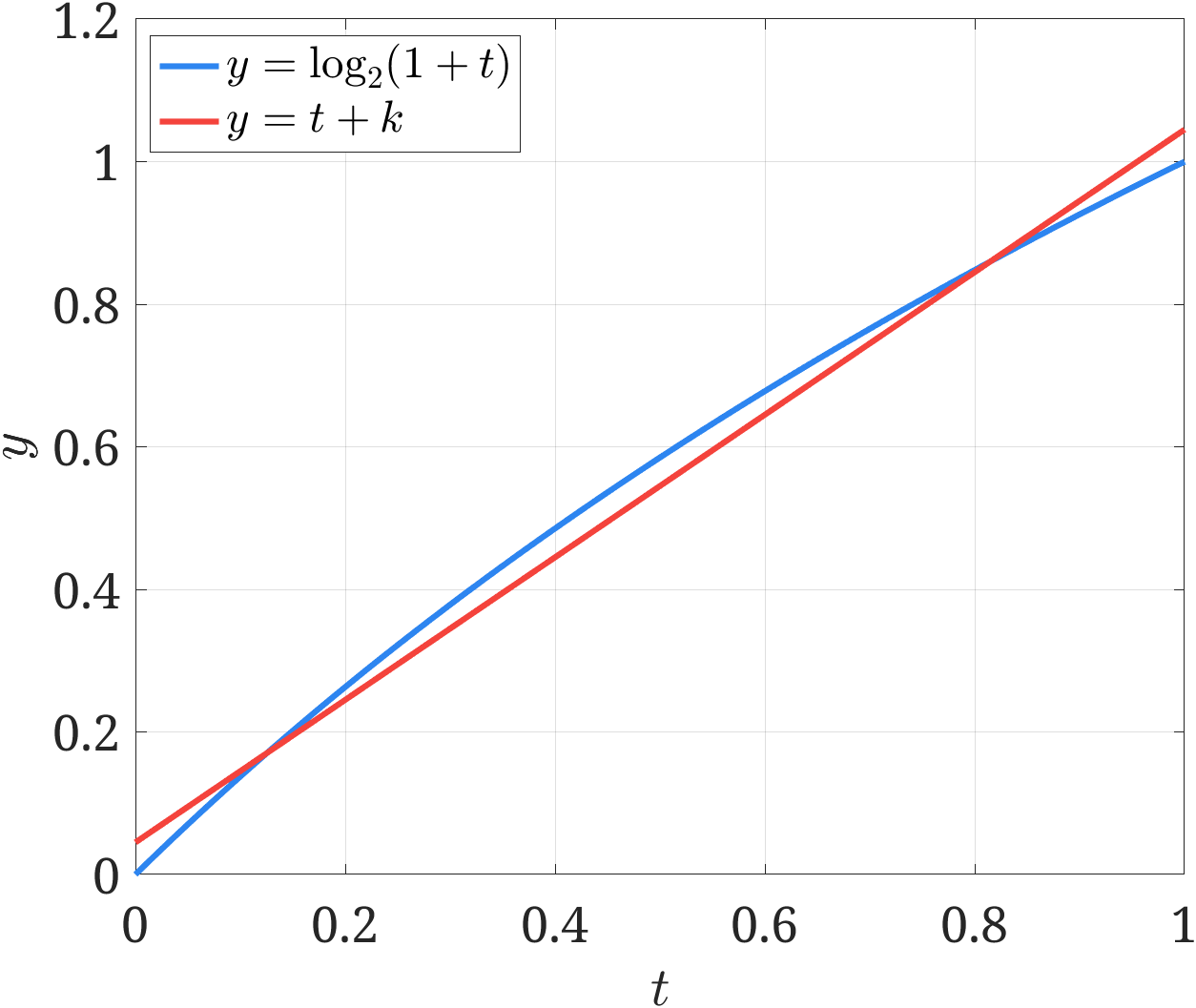
如此做，对数计算可以近似为

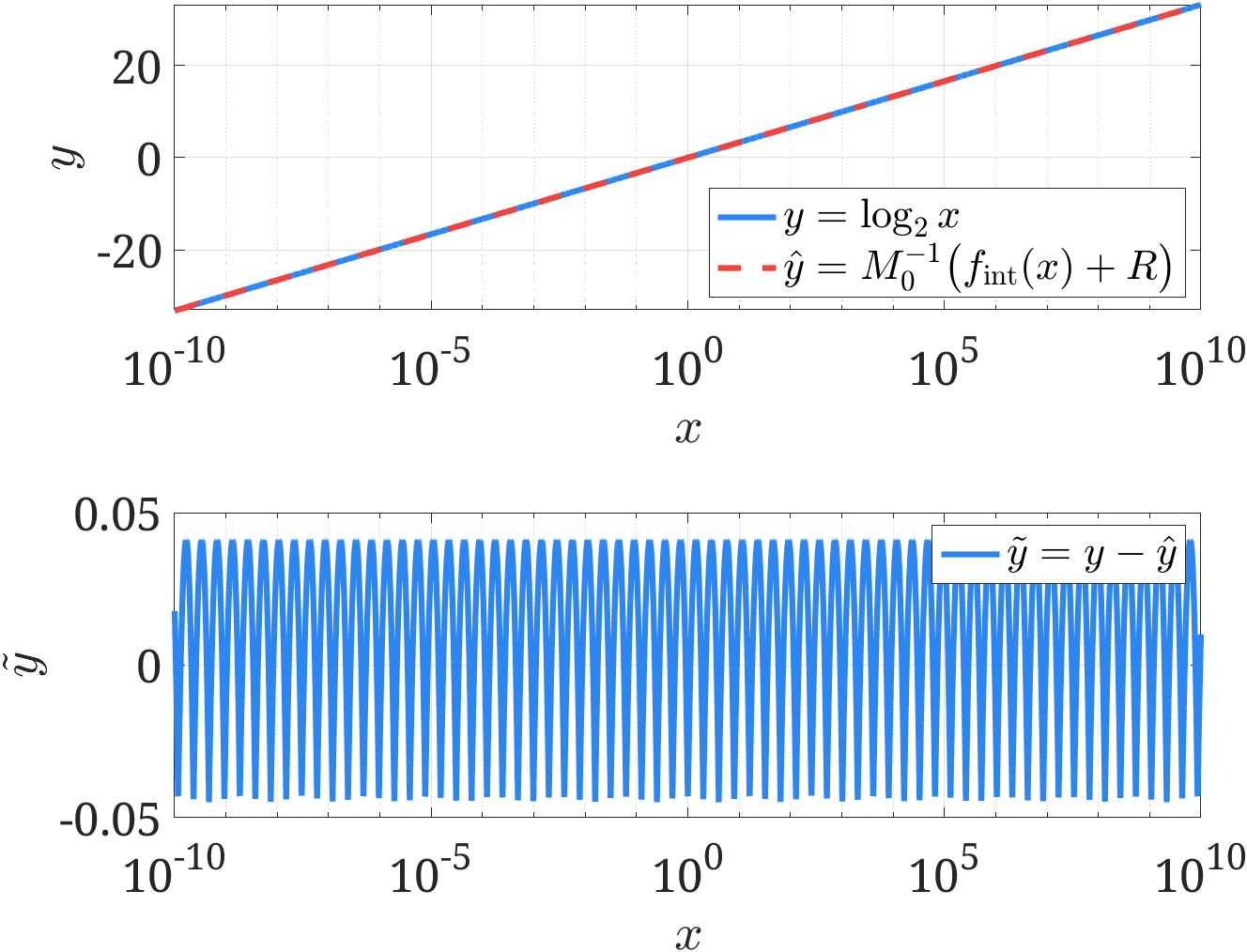
$$ \log_2 x \approx E-E_0 + \frac{M}{M_0} + k = \frac{1}{M_0} \biggl( \underbrace{EM_0 + M}_{f_{\mathrm{int}}(x)} + \underbrace{M_0 \left( k-E_0 \right)}_{R} \biggr) $$

式中，$EM_0 + M$ 是将浮点数 $x$ 的指数位和小数位合在一起进行二进制转化得到的整数，即所谓的强制类型转换，用函数记作 $f_{\mathrm{int}}(x)$。

由此我们可以得到一个重要结论：浮点数的对数与其强制类型转化后的整数存在线性近似，因此可以利用强制类型转换对对数计算进行快速估计。如下图所示，在 $x\in[10^{-10}, 10^{10}]$ 范围内的估计误差不超过 $0.05$。

注意

我们在对 $\log_2 (1+t)$ 进行线性近似时人为规定了斜率为 $1$，只有这样 $\log_2 x$ 才与强制类型转化之后的结果 $EM_0 +M$ 相关。若取 $\log_2(1+t) \approx at + k, (a\ne 1)$，$M$ 将替换为 $aM$，需要对小数部分做额外的乘法，与直接进行强制数据类型转换相比引入了额外的计算，会降低程序效率。

快速求解平方根的倒数

利用强制类型转换获得对数的初步估计值后，可以利用牛顿迭代获得更高精度的值。在此我们讨论另一种常用的应用：快速计算平方根的倒数，其有名的 C 代码如下所示。

float Q_rsqrt( float number )
{
    long i;
    float x2, y;
    const float threeHalfs = 1.5f;

    x2 = number * 0.5f;
    y  = number;
    i  = * ( long * ) &y;                       // evil floating point bit level hacking
    i  = 0x5f3759df - ( i >> 1 );               // What the fuck? 
    y  = * ( float * ) &i;
    y  = y * ( threeHalfs - ( x2 * y * y ) );   // 1st iteration
//  y  = y * ( threeHalfs - ( x2 * y * y ) );   // 2nd iteration, this can be removed

    return y;
}

现在我们用强制类型转换与对数的关系来解释这个代码：

使用将原问题取对数变成线性问题：

$$ y = \frac{1}{\sqrt{x}} \quad \rightarrow \quad \log_2 y = - \frac{1}{2} \log_2 x $$

将对数用强制进制转化近似，更新线性关系（C 代码中，除以二可以使用右移位得到）：

$$ \left.\begin{aligned} \log_2 x &\approx \frac{1}{M_0} \left( f_{\mathrm{int}}(x) + R \right) \\ \log_2 y &\approx \frac{1}{M_0} \left( f_{\mathrm{int}}(y) + R \right) \end{aligned} \right\} \quad \rightarrow \quad f_{\mathrm{int}}(y_0) = - \frac{3}{2} R - \frac{1}{2} f_{\mathrm{int}}(x) $$

其中 $-\frac{3}{2}R = \frac{3}{2}M_0(E_0-k)$，对于单精度数，取 $k=0.045$ 时，用十六进制表示为 0x5f3759df，这就是代码中“魔法数”的由来。

反向使用强制进制转化得到原数（平方根的倒数）初值：

$$ y_0 = f_{\mathrm{int}}^{-1}(y_0) = f_{\mathrm{int}}^{-1}\left( -\frac{3}{2} R - \frac{1}{2} f_{\mathrm{int}}(x) \right) $$

构造牛顿迭代提高求解精度：

原问题可以转化为函数 $f(y) = 1/y^2 -x$ 的零点问题，因此牛顿迭代为

$$ y_{i+1} = y_i - \frac{f(y_i)}{f'(y_i)} = y_i \left( \frac{3}{2} - \frac{x}{2} y_i^2 \right) $$

牛顿迭代的收敛速度很快，并且由于对数近似对初值的估计较为准确，所以只需要进行简单的一次或两次迭代就可以达到足够的精度。最后给出验证结果，如下图所示，可见利用强制类型转换已经获取足够的精度了，两次牛顿迭代后可以将误差进一步缩小到 $10^{-5}$ 以下，简单且高效。

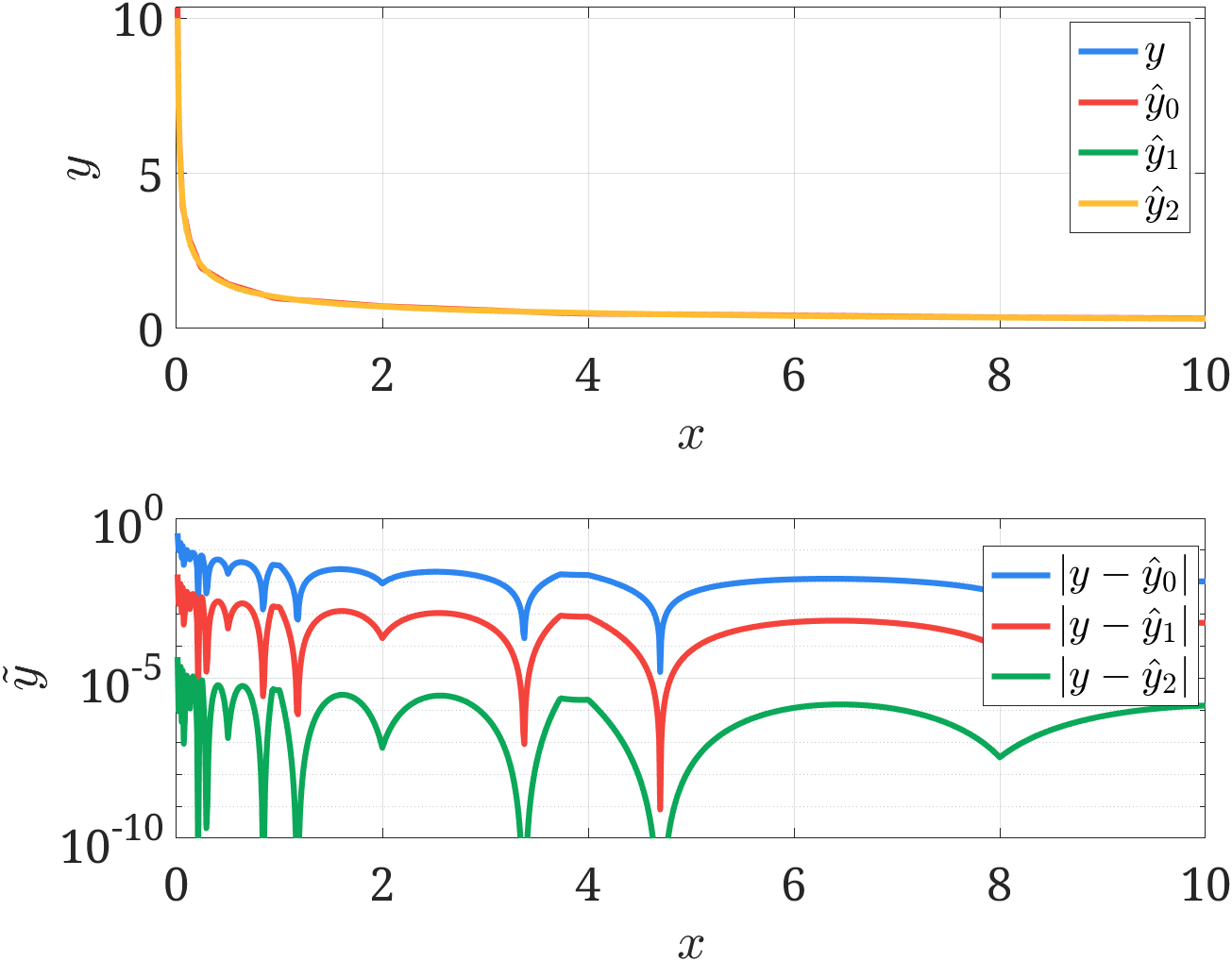
本文相关的 MATLAB 代码我放在了 GitHub 仓库，欢迎讨论交流。

参考资料

MathWorks Inc., Floating-Point Numbers.
爱XR的麦子, 【回归本源】番外1-雷神之锤3的那段代码.
Chris Lomont, Fast Inverse Square Root, 2003.