鲁棒跟踪控制

对于被引入到系统的参考信号，如果其特征是已知的，还可以采用所谓的鲁棒跟踪控制进一步提高系统对该类信号的跟踪能力。本文将介绍这种方法的设计。

参考信号特征

参考信号的特征可以用一定的微分方程进行描述。例如直流信号可以不失一般性地描述为 $\dot{r}=0$；而正弦信号可以参考弹簧-刚度系统的描述；如果参考信号为 $\omega_1$ 和 $\omega_2$ 两个正弦信号的叠加，它的微分方程可选为

$$r^{(4)}+(\omega_1^2+\omega_2^2)r^{(2)} + \omega_1^2\omega_2^2 =0$$

用于描述信号特征的微分方程有很多，依信号类型而不同。本文以一个二阶信号为例，假设输入的参考信号满足微分方程

$$\ddot{r} + \alpha_1 \dot{r} +\alpha_0 r = 0$$

根据该微分方程，可以对控制律或这状态估计器进行扩展，从而实现鲁棒跟踪控制（Robust Tracking Control）。

扩展控制律

设被控对象的状态空间表述为

$$ \left\{ \begin{aligned} \dot{\bm{x}} &= A \bm{x} + Bu \\ y &= C \bm{x} \end{aligned} \right. $$

定义跟踪误差 $e=y-r$ 。将其代入参考信号的微分方程，有

$$ \begin{aligned} \ddot e + {\alpha _1}\dot e + {\alpha _0}e &= \ddot y + {\alpha _1}\dot y + {\alpha _0}y \\ &= {C}\left( {\ddot{\bm{x}} + {\alpha_1}\dot{\bm{x}} + {\alpha _0}{\bm{x}}} \right) \\ &= {C\bm{\xi }} \\ \end{aligned} $$

这里定义了 $\xi={\ddot{\bm{x}} + {\alpha_1}\dot{\bm{x}} + {\alpha _0}{\bm{x}}}$，考察它的动态，有

$$ \begin{aligned} \dot{\xi} &= \frac{\mathrm{d}}{\mathrm{d}t} \left( \ddot{\bm{x}} + \alpha_1 \dot{\bm{x}} +\alpha_0 \bm{x}\right) \\ &= \frac{\mathrm{d}^2}{\mathrm{d}t^2} \dot{\bm{x}} + \alpha_1 \frac{\mathrm{d}}{\mathrm{d}t} \dot{\bm{x}} + \dot{\bm{x}} \\ &=A\left( \ddot{\bm{x}} + \alpha_1 \dot{\bm{x}} +\alpha_0 \bm{x}\right) + B \left( \ddot{u} + \alpha_1 \dot{u} +\alpha_0 u\right) \\ &= A \xi + B \mu \end{aligned} $$

同样补充定义了 $\mu = \ddot u + \alpha \dot u + \alpha_0 u$ 。

综上，利用误差和扩展的状态量构造误差空间（Error Space）

$$ {\bm{\dot z}} = {{ A}_z}{\bm{z}} + {{B}_z}\mu = \begin{bmatrix} 0&1&{0}\\\ { - {\alpha _0}}&{ - {\alpha _1}}&{C}\\\ {0}&{0}&{ A} \end{bmatrix} \left[ \begin{array}{c} e \\ \dot{e} \\ \xi \end{array} \right] + \begin{bmatrix} 0\\\ 0\\\ {B} \end{bmatrix} \mu $$

取状态反馈为 $\mu = - {{K}_z}{\bm{z}} = - \begin{bmatrix} {{K_{e0}}}&{{K_{e1}}}&{{{K}_x}} \end{bmatrix}\bm{z}$，当上述误差收敛时，由于跟踪误差为零，系统的输出将跟随输入。

为了实现上述控制器，需要从 $\mu$ 中求解系统输入 $u$ ，这可以从 $\mu$ 的定义中获得

$$ \begin{gathered} \ddot u + {\alpha _1}\dot u + {\alpha _0}u = - {{K}_z}{\bm{z}} = - {K_{e0}}e - {K_{e1}}\dot e - {K}_x\left( \ddot{\bm{x}} + {\alpha _1}\dot{\bm{x}} + {\alpha _0}{\bm{x}} \right) \\ \Updownarrow \\ \frac{{{{\text{d}}^2}}}{{{\text{d}}{t^2}}}\left( {u + {{K}_x}{\bm{x}}} \right) + {\alpha _1}\frac{{\text{d}}}{{{\text{d}}t}}\left( {u + {{K}_x}{\bm{x}}} \right) + {\alpha _0}\left( {u + {{K}_x}{\bm{x}}} \right) = - {K_{e0}}e - {K_{e1}}\dot e \\ \Downarrow \\ e \to u + {{K}_x}{\bm{x}}:\quad H(s) = - \frac{{{K_{e1}}s + {K_{e0}}}}{{{s^2} + {\alpha _1}s + {\alpha _0}}} \\ \end{gathered} $$

利用微分方程的实现手段（传递函数或状态空间的标准实现），根据 $e$ 求解 $u + {{K}_x}{\bm{x}}$ ，然后与 ${{K}_x}{\bm{x}}$ 相减即可得到系统的输入信号 $u$ 。这种方法可以看作是对控制律的扩展，而状态估计器与一般的估计器并无大异，可以将这种方法命名为扩展控制律，其结构如下图所示。

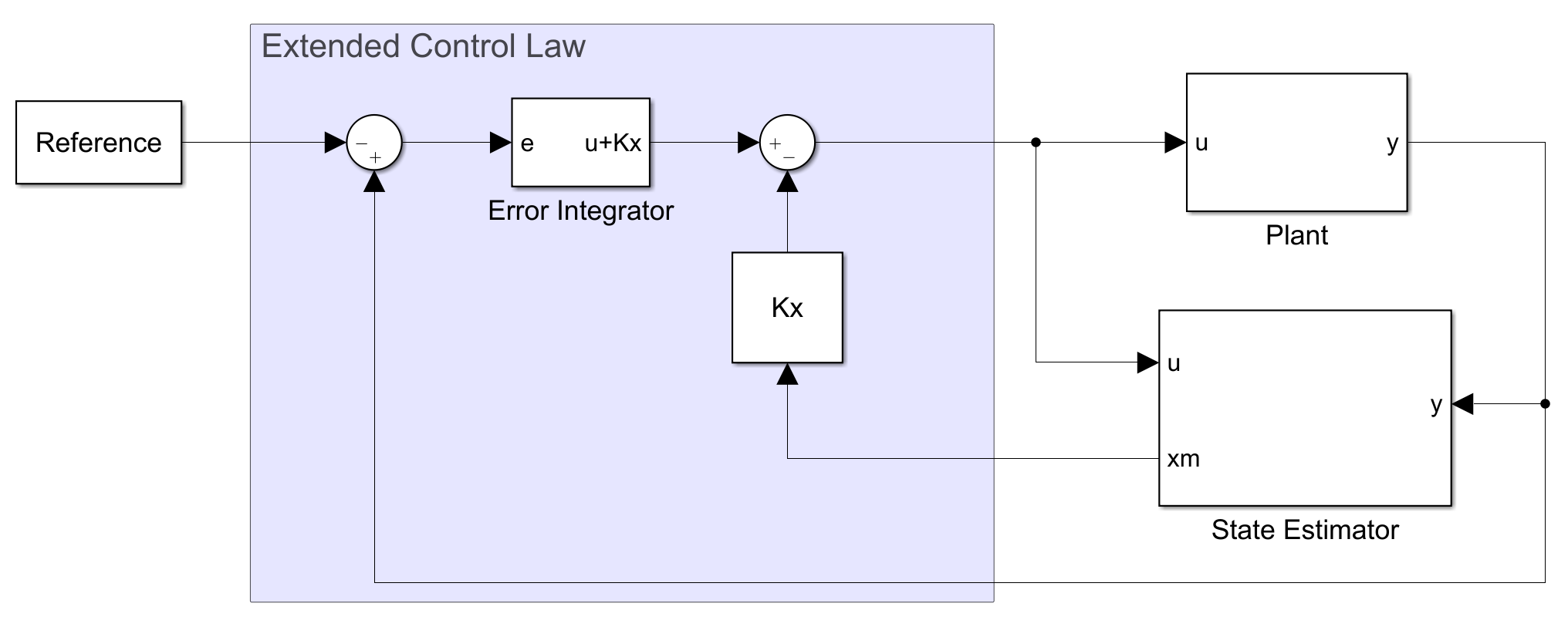
扩展状态估计器

既然控制律可以利用已知的参考信号动态进行扩展，那么状态估计器也应当能够扩展。我们可以这样想：如果系统的输出与参考之间存在误差，说明系统的输入端存在没有被完全抵消的扰动 $\rho$ ，如果能够对这个扰动进行估计，令 $u=-K\bm{x}-\rho$ 就可以在控制器的输出端抵消这个扰动，从而减小跟踪误差。

从系统的输出向输入看，表现为各微分的组合，当参考信号 $r$ 满足某个微分方程时， $\rho$ 也一定会满足该微分方程，在本例中

$$\ddot{\rho} + \alpha_1 \dot{\rho} +\alpha_0 \rho = 0$$

类似扩展控制律，将扰动和系统状态合一起作为扩展状态，状态空间可表述为

$$ \left\{ \begin{aligned} \bm{\dot{z}} &= {{A}_z}{\bm{z} + {{B}_z}u = \begin{bmatrix} 0&1&{\bm{0}} \\ { - {\alpha _0}}&{ - {\alpha _1}}&{\bm{0}} \\ {B}&{\bm{0}}&{A} \end{bmatrix}\begin{bmatrix} \rho \\ {\dot{\rho} } \\ {\bm{x}} \end{bmatrix} + \begin{bmatrix} 0 \\ 0 \\ {B} \end{bmatrix}u{\quad}} \\ y &= {{C}_z}{\bm{z} = \begin{bmatrix} 0&0&{C} \end{bmatrix}{\bm{z}}} \end{aligned}\right. $$

其对应的扩展状态估计器为

$$\dot{\bm{\hat{z}}} = {{A}_z}{\bm{z}} + {{B}_z}u + {L}_z\left( {y - {{C}_z}{\bm{z}}} \right)$$

利用 ${{A}_z} - {{L}_z}{{C}_z}$ 的特征值设计使扩展状态估计器稳定，最后用 $u=-K\hat{\bm{x}} - \hat{\rho}$ 即可完成整个控制器设计。本例中的闭环框图如下，状态估计器相对于普通的状态估计器增加了对扰动的建模，因此称为扩展状态估计器。

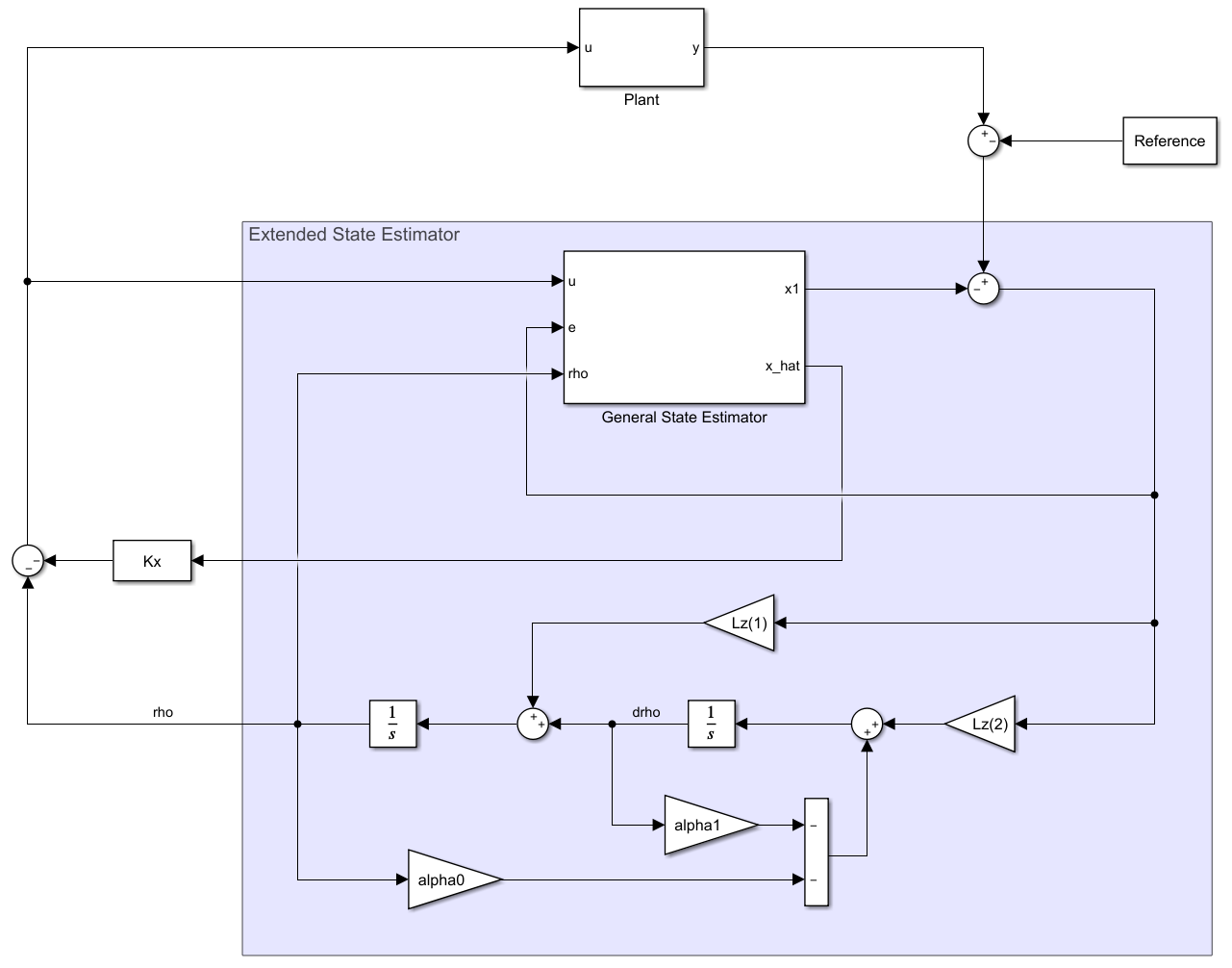
参考文献

1. G.F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. 2014.