四元数与三维旋转

复数在处理平面内旋转时具有很简洁的形式，然而复数只有两个自由度，无法处理三维空间内的旋转。为了将复数用于旋转的思想扩展到三维情况，四元数由此诞生。本文简要介绍四元数及其运算规则，推导四元数处理三维旋转的一般形式。

复数与二维旋转

在平面参考系 $\mathscr{E} = \{\vec{e}_1, \vec{e}_2 \}$ 中，设矢量 $\vec{a}$ 的坐标为 $\bm{a} = [a_1, a_2]^\mathrm{T}$。先将参考系基矢分别映射为复平面的实轴和虚轴，则矢量的坐标可以用复数表示为

$$ \bm{a} = a_1 + a_2 i = a \mathrm{e}^{i \alpha} $$

其中 $a$ 为矢量 $\vec{a}$ 的模长，$\alpha$ 为其与实轴（即 $\vec{e}_1$）的夹角。利用指数的计算规则，将 $\vec{a}$ 逆时针旋转 $\varphi$ 后得到的向量 $\vec{b}$ 在同一参考系下的坐标可以表示为

$$ \bm{b} = a \mathrm{e}^{i (\alpha+\varphi)} = \mathrm{e}^{i \varphi} a \mathrm{e}^{i \alpha} = \mathrm{e}^{i \varphi} \bm{a} $$

显然，单位模长的复数 $\mathrm{e}^{i\varphi}$ 可以很方便地处理平面内矢量的旋转。通常的复数只有一个实部和一个虚部，也就是只有两个自由度。然而空间旋转为三个自由度，因此需要对复数进行扩充，就有了本文将重点讨论的四元数。

矩阵形式的旋转

在正式讨论四元数之前，有必要先推导矩阵形式下的矢量旋转，其结论将与后面四元数形式的旋转紧密结合。

欧拉定理告诉我们，空间内的任意旋转都可以等价为绕一个方向旋转一个角度。设任意矢量 $\vec{a}$ 绕单位矢量 $\vec{v}$ 旋转 $\varphi$ 角度后得到 $\vec{b}$，如下图所示

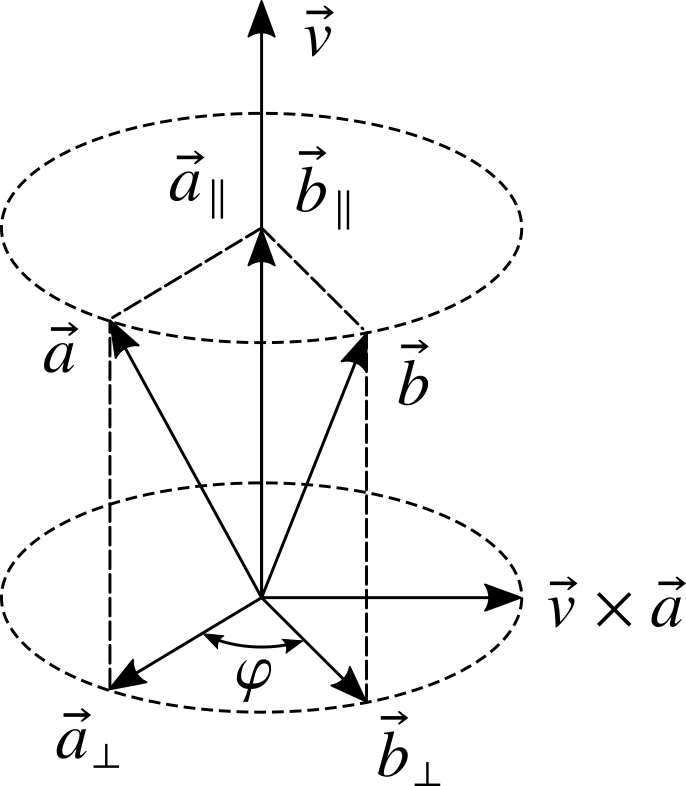
我们将矢量 $\vec{a}$ 分解为平行于 $\vec{v}$ 的 $\vec{a}_\parallel$ 和垂直于 $\vec{v}$ 的 $\vec{a}_\perp$，分别将其旋转后组合即可得到 $\vec{b}$。

平行于转轴的分量 $\vec{a}_\parallel$ 旋转后保持不变，即

$$ \vec{b}_\parallel = \vec{a}_\parallel = (\vec{v} \cdot \vec{a}) \vec{v} $$

任意选定参考系，上式的坐标形式可以写为

$$ \bm{b}_\parallel = \bm{a}_\parallel = (\bm{v}^\mathrm{T} \bm{a}) \bm{v} = \bm{v}(\bm{v}^\mathrm{T} \bm{a}) = (\bm{v} \bm{v}^\mathrm{T} )\bm{a} $$

垂直于转轴的分量 $\vec{a}_\perp$ 旋转后，根据上图所示，在 $\vec{a}_\perp$ 和 $\vec{v}\times\vec{a}$ 构成的平面内（注意这两个基矢正交，且模长相等），有

$$ \vec{b}_\perp = \vec{a}_\perp \cos\varphi + \vec{v}\times\vec{a}_\perp \sin\varphi = \vec{a}_\perp \cos\varphi + \vec{v}\times\vec{a} \sin\varphi $$

两个等号分别考虑了投影面第二基矢的等价表述，即 $\vec{v}\times\vec{a}_\perp = \vec{v}\times\vec{a}$，写成坐标形式，有

$$ \begin{aligned} \bm{b}_\perp &= \cos\varphi \bm{a}_\perp + \sin\varphi \bm{v} \times \bm{a}_\perp = \left( \cos\varphi + \sin\varphi \bm{v} \times \right) \bm{a}_\perp \\ &= \cos\varphi (\bm{a} - \bm{a}_\parallel ) + \sin\varphi \bm{v} \times \bm{a} = \left( \cos\varphi \left(I - \bm{v} \bm{v}^\mathrm{T}\right) + \sin\varphi \bm{v} \times \right) \bm{a} \end{aligned} $$

上式第一行将与后面四元数推导进行对比，联立第二行结果与平行转轴分量的结果，旋转前后矢量的坐标关系为

$$ \bm{b} = \bm{b}_\parallel + \bm{b}_\perp = \left[ \left(1-\cos\varphi\right)\bm{v} \bm{v}^\mathrm{T} + \cos\varphi I + \sin\varphi \bm{v}\times \right] \bm{a} $$

于是由 $\vec{a}$ 向 $\vec{b}$ 的转动对应的矩阵为

$$ R_b^a = \left(1-\cos\varphi\right)\bm{v} \bm{v}^\mathrm{T} + \cos\varphi I + \sin\varphi \bm{v}\times $$

四元数基本运算

四元数由一个实部和三个虚部构成，设三个虚部分别为 $i,j,k$，其满足

$$ i^2 = j^2 = k^2 = ijk = -1 $$

我们用花体的变量表示四元数，可以写为

$$ \mathfrak{q} = q_0 + q_1 i + q_2 j + q_3 k \quad \rightarrow \quad \begin{bmatrix} q_0 \\ \bm{q} \end{bmatrix} $$

箭头右侧为四元数的哈密顿表述，其将实部作为列向量的第一个参数，三个虚部构成四元数的矢量部分。

在后文中，我们将使用符号 $\otimes$ 表示四元数乘法，并且约定当 $\otimes$ 作用于三维向量时，应当将三维向量扩充为实部为零的纯四元数，再根据四元数计算规则进行计算。利用四元数虚部的性质，我们可以将四元数乘法写成矩阵的形式，即

$$ \mathfrak{a} \otimes \mathfrak{b} = \begin{bmatrix} \begin{array}{c:ccc} a_0 & -a_1 & -a_2 & -a_3 \\ \hdashline a_1 & a_0 & -a_3 & a_2 \\ a_2 & a_3 & a_0 & -a_1 \\ a_3 & -a_2 & a_1 & a_0 \end{array} \end{bmatrix} \begin{bmatrix} b_0 \\ \hdashline b_1 \\ b_2 \\ b_3 \end{bmatrix} = \begin{bmatrix} a_0 & -\bm{a}^\mathrm{T} \\ \bm{a} & a_0 I + \bm{a}\times \end{bmatrix} \begin{bmatrix} b_0 \\ \bm{b} \end{bmatrix} $$

类似于矩阵乘法，四元数乘法满足结合律，但一般不满足交换律。同样地，若两个四元数相乘得到 $1$，则称两个四元数互逆，记为 $\mathfrak{q} \otimes \mathfrak{q}^{-1} = \mathfrak{q}^{-1} \otimes \mathfrak{q} = 1$。四元数的模定义为四个分量的平方和开方，即

$$ |\mathfrak{q}| = \sqrt{q_0^2 + q_1^2 + q_2^2 + q_3^2} = \sqrt{ q_0^2 + \bm{q}^\mathrm{T}\bm{q}} = \sqrt{\mathfrak{q} \otimes \mathfrak{q}^*} $$

其中 $\mathfrak{q}^* = [q_0, -\bm{q}]$ 为 $\mathfrak{q} = [q_0, \bm{q}]$ 的共轭。特别地，单位四元数 $|\mathfrak{q}| = 1$ 的逆与共轭相等，即 $\mathfrak{q}^{-1}=\mathfrak{q}^*$，这另上式最后的等号为 $1$ 即可以得出。

四元数下的旋转

为了推导四元数与旋转之家的关系，不妨分别看看四元数乘以不同矢量的效果。在给定参考系下，设四元数矢量部分的坐标为 $\bm{q}$ ，将四元数表示为 $\mathfrak{q} = [q_0, \bm{q}]$。同样，将矢量 $\bm{a}$ 分解为平行于 $\bm{q}$ 的分量 $\bm{a}_\parallel$ 和垂直分量 $\bm{a}_\perp$。

四元数平行分量的乘积为：

$$ \mathfrak{q} \otimes \bm{a}_\parallel = \begin{bmatrix} q_0 & -\bm{q}^\mathrm{T} \\ \bm{q} & q_0 I + \bm{q}\times \end{bmatrix} \begin{bmatrix} 0 \\ \bm{a}_\parallel \end{bmatrix} = \begin{bmatrix} - \bm{q}^\mathrm{T} \bm{a}_\parallel \\ q_0 \bm{a}_\parallel \end{bmatrix} = \begin{bmatrix} 0 & -\bm{a}_\parallel^\mathrm{T} \\ \bm{a}_\parallel & \bm{a}_\parallel \times \end{bmatrix} \begin{bmatrix} q_0 \\ \bm{q} \end{bmatrix} = \bm{a}_\parallel \otimes \mathfrak{q} $$

这个公式虽然没有表现出对 $\bm{a}_\parallel$ 的旋转作用，但得到了一个重要结论：如果矢量与四元数的矢量部分平行，那么两者的四元数乘法满足交换律，即 $\mathfrak{q} \otimes \bm{a}_\parallel = \bm{a}_\parallel \otimes \mathfrak{q}$。

四元数垂直分量的乘积为：

$$ \mathfrak{q} \otimes \bm{a}_\perp = \begin{bmatrix} q_0 & -\bm{q}^\mathrm{T} \\ \bm{q} & q_0 I + \bm{q}\times \end{bmatrix} \begin{bmatrix} 0 \\ \bm{a}_\perp \end{bmatrix} = \begin{bmatrix} 0 \\ \left(q_0 + \bm{q} \times \right)\bm{a}_\perp \end{bmatrix} = \begin{bmatrix} 0 & -\bm{a}_\perp^\mathrm{T} \\ \bm{a}_\perp & \bm{a}_\perp \times \end{bmatrix} \begin{bmatrix} q_0 \\ -\bm{q} \end{bmatrix} = \bm{a}_\perp \otimes \mathfrak{q}^* $$

从最两端的等号可以得到“共轭交换律”：如果矢量与四元数的矢量部分垂直，那么两者的四元数乘法满足“共轭交换律”，即 $\mathfrak{q} \otimes \bm{a}_\perp = \bm{a}_\perp \otimes \mathfrak{q}^*$。现在我们仔细观察中间结果，可以发现 $\mathfrak{q} \otimes \bm{a}_\perp$ 依然是纯四元数，其矢量部分与上述矩阵形式下的旋转具有非常相似的结构：

$$ \left(q_0 + \bm{q} \times \right)\bm{a}_\perp \sim \left( \cos\varphi + \sin\varphi \bm{v} \times \right) \bm{a}_\perp $$

由此可知，若取 $\mathfrak{q} = [\cos\varphi, \sin\varphi \bm{v}]$，则 $\mathfrak{q} \otimes \bm{a}_\perp$ 的矢量部分就是将 $\bm{a}_\perp$ 沿着矢量 $\bm{v}$ 转动 $\varphi$ 角度之后的结果。因此，形如 $\mathfrak{q}(\theta) = [\cos\theta, \sin\theta \bm{v}]$ （$\bm{v}$ 为单位矢量）的四元数可以用于矢量的旋转操作，容易证明这是一个单位四元数，且存在以下等式

$$ \mathfrak{q}(\theta) \otimes \mathfrak{q}(\theta) = \begin{bmatrix} \cos\theta & -\sin\theta\bm{v}^\mathrm{T} \\ \sin\theta\bm{v} & \cos\theta I + \sin\theta\bm{v}\times \end{bmatrix} \begin{bmatrix} \cos\theta \\ \sin\theta \bm{v} \end{bmatrix} = \begin{bmatrix} \cos 2\theta \\ \sin 2\theta \bm{v} \end{bmatrix} = \mathfrak{q}(2\theta) $$

最后，为了得到更一般矢量的四元数旋转，结合上面的结论可知，将 $\bm{a}$ 绕 $\bm{v}$ 旋转 $\varphi$ 后的矢量的坐标 $\bm{b}$ 为

$$ \begin{aligned} \bm{b} &= \bm{b}_\parallel + \bm{b}_\perp \\ &= \bm{a}_\parallel + \mathfrak{q}(\varphi) \otimes \bm{a}_\perp \\ &= \mathfrak{q}(\frac{1}{2}\varphi) \otimes \mathfrak{q}^{-1}(\frac{1}{2}\varphi) \otimes \bm{a}_\parallel + \mathfrak{q}(\frac{1}{2}\varphi) \otimes \mathfrak{q}(\frac{1}{2}\varphi) \otimes \bm{a}_\perp \\ &= \mathfrak{q}(\frac{1}{2}\varphi) \otimes \bm{a}_\parallel \otimes \mathfrak{q}^{-1}(\frac{1}{2}\varphi) + \mathfrak{q}(\frac{1}{2}\varphi) \otimes \bm{a}_\perp \otimes \mathfrak{q}^*(\frac{1}{2}\varphi) \\ &= \mathfrak{q}(\frac{1}{2}\varphi) \otimes \bm{a}_\parallel \otimes \mathfrak{q}^{-1}(\frac{1}{2}\varphi) + \mathfrak{q}(\frac{1}{2}\varphi) \otimes \bm{a}_\perp \otimes \mathfrak{q}^{-1}(\frac{1}{2}\varphi) \\ &= \mathfrak{q}(\frac{1}{2}\varphi) \otimes \left( \bm{a}_\parallel + \bm{a}_\perp \right)\otimes \mathfrak{q}^{-1}(\frac{1}{2}\varphi) \\ &= \mathfrak{q}(\frac{1}{2}\varphi) \otimes \bm{a} \otimes \mathfrak{q}^{-1}(\frac{1}{2}\varphi) \end{aligned} $$

上式的推导中用到了四元数与平行、垂直矢量相乘的交换律，以及“单位四元数的逆与其共轭相等”的结论。由此可见，任意矢量绕 $\bm{v}$ 旋转 $\varphi$ 应当由四元数 $\mathfrak{q}(\varphi/2) = [\cos(\varphi/2), \sin(\varphi/2) \bm{v}]$ 表述。由 $\bm{a}$ 到 $\bm{b}$ 的旋转可以由矩阵和四元数分别表示为

$$ \bm{b} = R_b^a \bm{a} = \mathfrak{q}_b^a \otimes \bm{a} \otimes (\mathfrak{q}_b^a)^{-1} = \mathfrak{q}_b^a \otimes \bm{a} \otimes (\mathfrak{q}_a^b) $$

最后，考虑旋转矩阵与四元数之间的关系为

$$ \begin{aligned} R(\mathfrak{q}_b^a) = R_b^a &= \left(1-\cos\varphi\right)\bm{v} \bm{v}^\mathrm{T} + \cos\varphi I + \sin\varphi \bm{v}\times \\ &= 2 \sin^2\frac{\varphi}{2} \bm{v} \bm{v}^\mathrm{T} + \left(\cos^2\frac{\varphi}{2} - \sin^2\frac{\varphi}{2}\right) I + 2 \sin\frac{\varphi}{2}\cos\frac{\varphi}{2} \bm{v}\times \\ &\downarrow \quad \bigl( q_0=\cos\frac{\varphi}{2},\, \bm{q} = \sin\frac{\varphi}{2} \bm{v} \bigr) \\ &= 2 \bm{q} \bm{q}^\mathrm{T} + \left(q_0^2 - \bm{q}^\mathrm{T} \bm{q} \right) + 2 q_0 \bm{q} \times \\ &= \begin{bmatrix} q_0^2+q_1^2-q_2^2-q_3^2 & 2(q_1q_2-q_0q_3) & 2(q_0q_2+q_1q_3)\\ 2(q_0q_3+q_1q_2) & q_0^2-q_1^2+q_2^2-q_3^2 & 2(q_2q_3-q_0q_1)\\ 2(q_1q_3-q_0q_2) & 2(q_0q_1+q_2q_3) & q_0^2-q_1^2-q_2^2+q_3^2 \end{bmatrix} \end{aligned} $$

连续旋转的讨论

一个物体多次旋转，旋转矩阵（或四元数）应当是左乘还是右乘？在 坐标变换与矢量旋转 中我们给出的结论是右乘（同参考资料1），而按照这次推导的逻辑：$\bm{v}_0$ 旋转一次得到 $\bm{v}_1 = R_1 \bm{v}_0$，再将 $\bm{v}_1$ 旋转得到 $\bm{v}_2 = R_2 \bm{v}_1 = R_2 R_1 \bm{v}_0$……以此类推，连续转动时似乎应当左乘（同参考资料2），与之前的结论相反。这应当作何解释？

• 两者的关注点不同

如果将连续旋转按右乘的方式并和，最终得到的是矩阵，描述的是参考系（基矢）之间的关系：$\vec{B} = \vec{A} R^a_b$；而如果连续左乘，最右边项一定是某个待旋转的矢量的坐标，最后得到的结果是旋转之后的矢量在同一个坐标系下的坐标。

• 连续旋转的方向矢量坐标不同

在得到“连续左乘”的结论时，我们实际上选定了同一个参考系。从四元数 $\mathfrak{q} = [\cos(\varphi/2), \sin(\varphi/2) \bm{v}]$ 的角度来看，每一次旋转的转轴方向 $\vec{v}$ 的坐标 $\bm{v}$ 都是在同一个参考系 $\mathscr{E}$ 进行表达的；而连续右乘时，后一次旋转的转轴方向是在上一次转动之后的参考系中表达的。

$$ $$

参考文献

1. E. Canuto, C. Novara, D. Carlucci, C.P. Montenegro, L. Massotti, Spacecraft Dynamics and Control: The Embedded Model Control Approach, Butterworth-Heinemann, 2018.
2. Krasjet, A brief introduction to the quaternions and its applications in 3D geometry.
3. 3Blue1Brown, 四元数的可视化.