|
文章 分类 标签 关于
|

目录

目录

正交投影——极小化问题的解决方案

大春雨 avatar  收录于  类别 奇妙的数学
     约 1423 字   预计阅读 7 分钟 

“近似”是非常常用的数学手段，其中包括利用多项式来作为其他函数的近似，并使得两个函数之间的某个误差最小，这类极小化问题应当如何求解？本文从一个几何例子开始，以数形结合的思想初步给出极小化问题与正交投影之间的关系；然后介绍多项式的内积定义，给出函数在多项式线性空间的正交投影计算方法；最后以正弦函数的多项式近似给出一个极小化问题的实例。

如下图所示，三维空间中存在某一向量 v⃗\vec{v}，现需要在给定平面内找到一个向量 u⃗\vec{u} 来尽可能逼近 v⃗\vec{v}，这就要求两者的误差最小。向量的误差可以用模长（欧几里得范数）来定量表述，其定义为

∥u⃗−v⃗∥=(u⃗−v⃗)⋅(u⃗−v⃗)\left\| \vec{u} - \vec{v} \right\| = \sqrt{(\vec{u} - \vec{v}) \cdot (\vec{u} - \vec{v})}

由于点到平面内的距离最短，那么这个极小化问题的解就是向量 v⃗\vec{v} 在给定平面内的正交投影，即 u⃗=v⃗p\vec{u}=\vec{v}_p 。

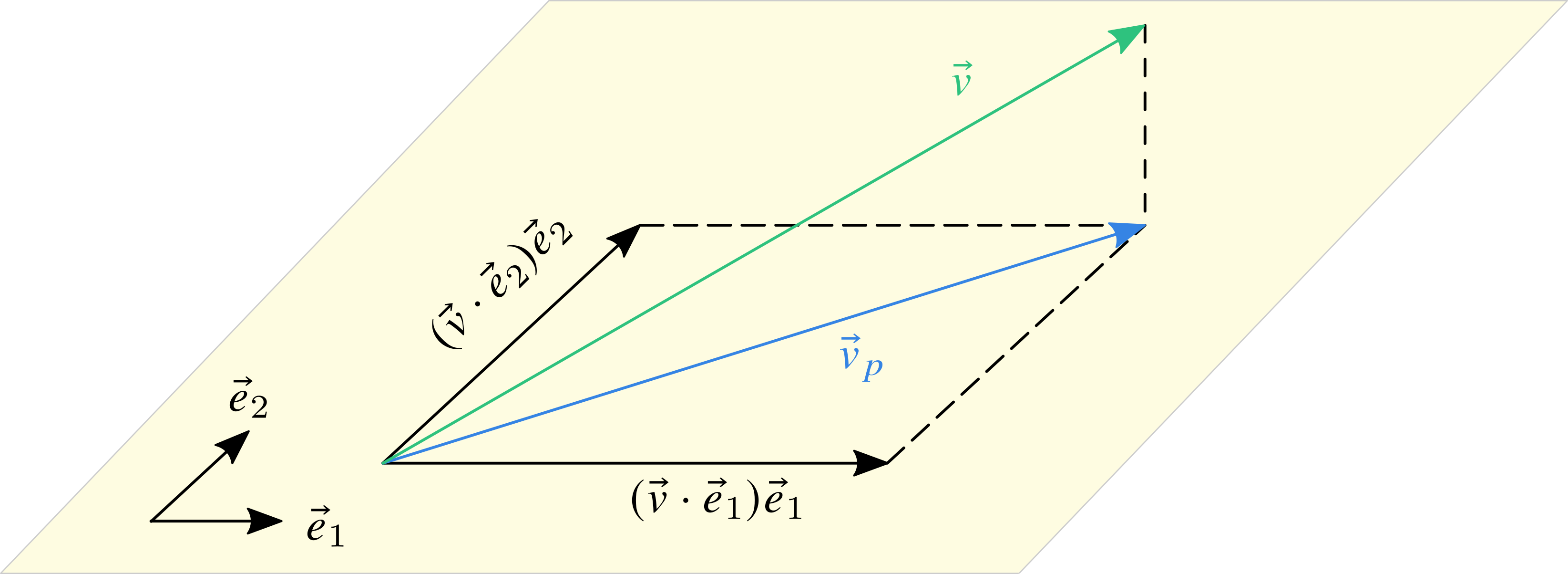空间向量的正交投影示意图

为了定量表述向量 v⃗\vec{v} 的正交投影，需要选取基向量，如图中的 e⃗1\vec{e}_1 和 e⃗2\vec{e}_2。特别地，所选取的基向量为标准正交基，即满足：

e⃗i⋅e⃗j={1(i=j)0(i≠j) \vec{e}_i \cdot \vec{e}_j = \left\{ \begin{matrix} 1 & (i = j) \\ 0 & (i \ne j) \end{matrix} \right.

在标准正交基下，正交投影可分解为

v⃗p=(v⃗p⋅e⃗1)e⃗1+(v⃗p⋅e⃗2)e⃗2\vec{v}_p = \left( \vec{v}_p \cdot \vec{e}_1 \right) \vec{e}_1 + \left( \vec{v}_p \cdot \vec{e}_2 \right) \vec{e}_2

由此可见，极小化问题可化为正交投影的求解问题，这涉及两点核心内容：1）构造合适的标准正交基；2）求原向量（也可能是函数）与各基的内积（对应向量的点乘）。

多项式的一般形式为

p=a0+a1x+a2x2+...+anxnp = a_0 + a_1x + a_2x^2 + ... + a_nx^n

向量可用坐标 xix_i 与基向量 e⃗i\vec{e}_i 的线性组合

v⃗=x1e⃗1+x2e⃗2+...+xne⃗n\vec{v} = x_1 \vec{e}_1 + x_2 \vec{e}_2 + ... + x_n \vec{e}_n

对比上面两种表述，若将 ai,(i=0,1,2…n)a_i , (i=0,1,2…n) 看作多项式的"坐标"，那么 xi,(i=0,1,2…n)x^i , (i=0,1,2…n) 就是多项式的基。容易看出这种表述确实满足线性可加原理，因而将 xix^i 作为多项式的基是合理的。

进一步，为了定义多项式的内积（用尖括号表示），同样由向量的内积类推可得

⟨u⃗, v⃗⟩=∑i=1nuivi→⟨p1(x), p2(x)⟩=∫p1(x)p2(x) dx \left\langle \vec{u},\,\vec{v} \right\rangle = \sum\limits_{i = 1}^n u_i v_i \to \left\langle p_1(x),\,p_2(x) \right\rangle = \int p_1(x)p_2(x)\,\mathrm{d}x

应当注意这里并没有给出多项式的内积定义的积分限，这通常由所关注的问题给出。

作为一个例子：求一个不超过5次的多项式 p5(x)p_5(x) ，使其在区间 [−π,,π]\left[-\pi,,\pi\right] 内逼近 sin⁡(x)\sin(x) ，要求 ∫−ππ(sin⁡(x)−p5(x))2,dx\int_{-\pi}^{\pi} \left(\sin(x)-p_5(x) \right)^2,\mathrm{d}x 最小。

观察到所需的最小值正是 sin⁡(x)\sin(x) 与 p5(x)p_5(x) 误差的内积，为了使其最小，p5(x)p_5(x) 就是 sin⁡(x)\sin(x) 在多项式线性空间的正交投影。

首先构造标准正交基。由上面讨论可知 xi(i=0,1,2…n)x^i (i=0,1,2…n) 是多项式的基，但可以验证其不是正交的，因为

∫−ππxixj dx≠{1(i=j)0(i≠j) \int_{ - \pi }^\pi x^i x^j\,\mathrm{d} x \ne \left\{ \begin{matrix} 1 & (i = j) \\ 0 & (i \ne j) \end{matrix} \right.

为此，可采用格拉姆-施密特正交化方法，基 viv_i 经过正交化后的标准正交基 eie_i 为

{e1=v1∥v1∥ei=vi−⟨vi, e1⟩e1−⟨vi, e2⟩e2−...−⟨vi, ei−1⟩ei−1∥vi−⟨vi, e1⟩e1−⟨vi, e2⟩e2−...−⟨vi, ei−1⟩ei−1∥(i>1) \left\{ \begin{aligned} e_1 &= \frac{v_1}{\left\| v_1 \right\|} \\ e_i &= \frac{ v_i - \left\langle v_i,\, e_1 \right\rangle e_1 - \left\langle v_i,\, e_2 \right\rangle e_2 - ... - \left\langle v_i,\, e_{i-1} \right\rangle e_{i-1} }{\left\| v_i - \left\langle v_i,\, e_1 \right\rangle e_1 - \left\langle v_i,\, e_2 \right\rangle e_2 - ... - \left\langle v_i,\, e_{i-1} \right\rangle e_{i-1} \right\| } \quad (i>1) \end{aligned} \right.

利用MATLAB符号计算可得本题的标准正交基可选为

{e0=22 πe1=62 π3/2xe2=−3 104 π5/2(π23−x2)e3=−5 144 π7/2(3 x π25−x3)e4=105 216 π9/2(x4−6 π2 x27+3 π435)e5=63 2216 π11/2(x5−10 π2 x39+5 π4 x21) \left\{\begin{aligned} e_0 &= \frac{\sqrt{2}}{2\,\sqrt{\pi }} \\ e_1 &= \frac{\sqrt{6}}{2\,\pi^{3/2} } x \\ e_2 &= -\frac{3\,\sqrt{10}}{4\,\pi^{5/2} } \left(\frac{\pi^2 }{3}-x^2 \right) \\ e_3 &= -\frac{5\,\sqrt{14}}{4\,\pi^{7/2} } \left(\frac{3\,x\,\pi^2 }{5}-x^3 \right) \\ e_4 &= \frac{105\,\sqrt{2}}{16\,\pi^{9/2} } \left(x^4 -\frac{6\,\pi^2 \,x^2 }{7}+\frac{3\,\pi^4 }{35}\right) \\ e_5 &= \frac{63\,\sqrt{22}}{16\,\pi^{11/2} } \left(x^5 -\frac{10\,\pi^2 \,x^3 }{9}+\frac{5\,\pi^4 \,x}{21}\right) \end{aligned}\right.

计算 sin⁡(x)\sin(x) 与各基的内积后，得所求的5次多项式为

p5(x)=(1058π2−160658π4+1559258π6)x+(−3154π4+393754π6−3638254π8)x3+(6938π6−727658π8+6548858π10)x5≈0.9878621356x−0.1552714106x3+0.005643117976x5  \begin{aligned} {p_5}(x) &= \left( {\frac{{105}}{{8{\pi ^2}}} - \frac{{16065}}{{8{\pi ^4}}} + \frac{{155925}}{{8{\pi ^6}}}} \right)x + \left( { - \frac{{315}}{{4{\pi ^4}}} + \frac{{39375}}{{4{\pi ^6}}} - \frac{{363825}}{{4{\pi ^8}}}} \right){x^3} + \left( {\frac{{693}}{{8{\pi ^6}}} - \frac{{72765}}{{8{\pi ^8}}} + \frac{{654885}}{{8{\pi ^{10}}}}} \right){x^5} \\ &\approx {\text{0}}{\text{.9878621356}}x - {\text{0}}{\text{.1552714106}}{x^3} + {\text{0}}{\text{.005643117976}}{x^5} \ \end{aligned}

上式可以与 sin⁡(x)\sin(x) 的泰勒展开对比

pt(x)=x−x36+x5120p_{t}(x) = x-\frac{x^3 }{6}+\frac{x^5 }{120}

将三者绘制在同一张图上，如下图所示，可见正交投影的方式获取的多项式更加逼近原始正弦函数，在 ±π\pm\pi 处的误差远小于泰勒展开导致的误差。

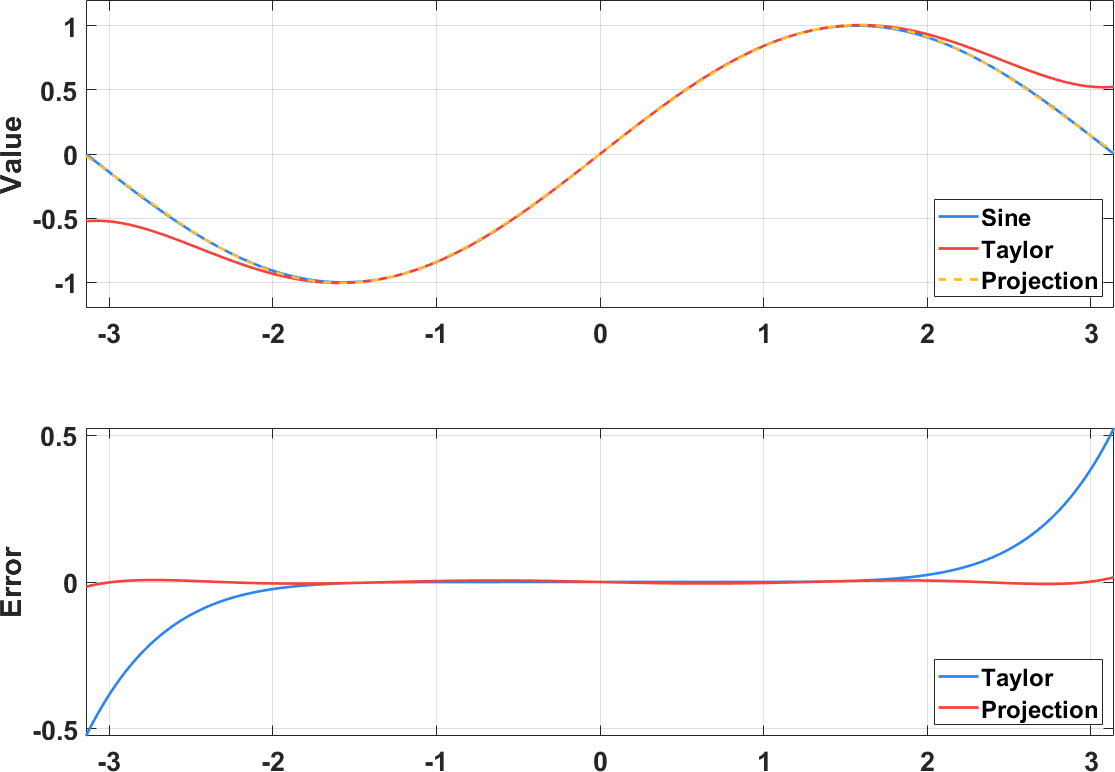正弦函数的多项式近似

本文所涉及的相关符号计算源码如下

matlab

% Symbolic calculation for projection of sin(x)
% Ref: (ISBN) 978-7-115-43178-3, 149-150

% XiaoCY 2020-08-02 (MATLAB R2020a)

clear;clc
close all

%% Symbolic Calculation
syms x
f(x) = sin(x);
degp = 5;               % degree of polynomial
B = x.^(0:degp);

% Gram－Schmidt Orthogonalization
B(1) = B(1)/sqrt(int(B(1)^2,-pi,pi));
for k = 2:degp+1
    V = B(k);
    for m = 1:k-1
        V = V-int(B(k)*B(m),-pi,pi)*B(m);
    end
    B(k) = V/sqrt(int(V^2,-pi,pi));
end

Y = int(f.*B,-pi,pi).*B;
y(x) = sum(Y);

p = sym2poly(y);
ft = taylor(f,x,0,'order',6);

%% Plot Results
x = linspace(-pi,pi,1e3);

figure
subplot(2,1,1)
plot(x,f(x),'DisplayName','Sine')
hold on
plot(x,ft(x),'DisplayName','Taylor')
plot(x,polyval(p,x),'DisplayName','Projection')
grid on
legend('Location','southeast')
ylabel('Value')
axis([-pi pi -1.2 1.2])

subplot(2,1,2)
plot(x,ft(x)-f(x),'DisplayName','Taylor')
hold on
plot(x,polyval(p,x)-f(x),'DisplayName','Projection')
grid on
legend('Location','southeast')
ylabel('Error')
xlim([-pi pi])
  1. Sheldon Axler. Linear Algebra Done Right (线性代数应该这样学). 2016.
更新于 2023-06-29
阅读原始文档
 正交投影, 曲线拟合
 | 主页