从牛顿方程到开普勒定律
开普勒定律揭示了行星围绕中心天体运动的规律,随后牛顿提出的运动学定律和万有引力定律进一步从原理上进行了解释。本文从牛顿方程的角度出发,基于限制性二体问题推导开普勒运动定律,被简要介绍轨道六要素和开普勒方程。
限制性二体问题
设两个质点 $m_0$、$m_1$ 的位置矢量分别为 $\vec{r}_0$ 和 $\vec{r}_1$。记万有引力常数为 $G$,并将质点的相对位置记为 $\vec{r}=\vec{r}_1 - \vec{r}_0$,则质点之间的万有引力分别为:
$$ \vec{G}_0 = \frac{Gm_0m_1}{r^2} \frac{\vec{r}}{r} ,\qquad \vec{G}_1 = -\frac{Gm_0m_1}{r^2} \frac{\vec{r}}{r} $$进一步考虑质点受到其他的作用力 $\vec{F}_0$ 和 $\vec{F}_1$,根据牛顿第二定律,有
$$ \left\{\begin{aligned} \ddot{\vec{r}}_0 &= \frac{Gm_1}{r^2} \frac{\vec{r}}{r} + \frac{\vec{F}_0}{m_0} \\ \ddot{\vec{r}}_1 &= -\frac{Gm_0}{r^2} \frac{\vec{r}}{r} + \frac{\vec{F}_1}{m_1} \end{aligned}\right. $$因此相对运动方程为
$$ \ddot{\vec{r}} = \ddot{\vec{r}}_1 - \ddot{\vec{r}}_0 = -\frac{G(m_0+m_1)}{r^2} \frac{\vec{r}}{r} + \frac{\vec{F}_1}{m_1} - \frac{\vec{F}_0}{m_0} $$当 $m_0 \gg m_1$ 时,上述方程可以简化为
$$ \ddot{\vec{r}} = -\frac{\mu}{r^2} \frac{\vec{r}}{r} + \frac{\vec{F}_1}{m_1} $$称之为限制性二体问题。为了表述的方便,将引力常数重新记为 $\mu = Gm_0$。更进一步,当 $\vec{F}_0 = \vec{0}$ 时,上述微分方程的通解称为轨道的自由响应,满足开普勒运动定律。后文将基于此假设推导开普勒定律。
更进一步,二体的质心运动满足
$$ \ddot{\vec{r}}_c = \frac{\mathrm{d}^2}{\mathrm{d}t^2} \left( \frac{m_0}{m_0+m_1}\vec{r}_0 + \frac{m_0}{m_0+m_1}\vec{r}_1 \right) = \frac{1}{m_0 + m_1} \left(\vec{F}_0 + \vec{F}_1\right) $$当外力 $\vec{F}_0 = \vec{F}_1 = \vec{0}$ 时,质心加速度为零,可以作为惯性参考系的原点。对于限制性二体问题,系统质心取为较大质量质点的质心,即中心天体的质心。
角动量守恒
由于限制性二体问题在外力 $\vec{F}_0 = \vec{0}$ 时只受到连线方向的引力作用,合力矩为零,因此其角动量 $\vec{h} = \vec{r} \times \vec{v}$ 守恒。我们可以从其导数为零(零向量)进行证明:
$$ \dot{\vec{h}} = \frac{\mathrm{d}}{\mathrm{d}t} \left( \vec{r} \times \vec{v} \right) = \dot{\vec{r}} \times \vec{v} + \vec{r} \times \dot{\vec{v}} = \vec{v} \times \vec{v} + \vec{r} \times \left( - \frac{\mu}{r^2} \frac{\vec{r}}{r} \right) = \vec{0} $$角动量守恒可以从两方面来看,首先,角动量的方向不变,意味着该方向可以作为(轨道)惯性参考系的基矢。习惯上取该方向为第三基矢 $\vec{p}_3=\vec{h}/h$,因此在该参考系下可以将角动量记为坐标形式,即 $\bm{h}^p = [0, 0, h]^\mathrm{T}$。
其次,角动量的大小不变。为了说明该性质的物理含义,考察下图所示在 $\mathrm{d}t$ 时间内运动质点与中心质点连线扫过的面积为
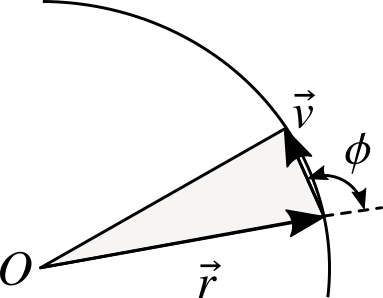
这意味着单位时间内连线扫过的面积为常数,用实例表述为:行星和太阳连线在相同的时间内扫过的面积相等。这就是开普勒第二定律。
离心率守恒
根据限定性二体问题的运动方程,移项后与角动量进行叉乘,有
$$ \begin{aligned} \vec{0} \times \vec{h} &= \left( \ddot{\vec{r}} + \frac{\mu}{r^3} \vec{r} \right) \times \vec{h} \\ &= \dot{\vec{v}} \times \vec{h} + \frac{\mu}{r^3} \vec{r} \times \left( \vec{r} \times \vec{v} \right) \\ &= \frac{\mathrm{d}}{\mathrm{d}t} \left(\vec{v}\times \vec{h} \right) + \frac{\mu}{r^3} \bigl( \left(\vec{r}\cdot\vec{v}\right) \vec{r} - \left(\vec{r}\cdot\vec{r}\right)\vec{v} \bigr) \\ &= \frac{\mathrm{d}}{\mathrm{d}t} \left(\vec{v}\times \vec{h} \right) + \frac{\mu}{r^3} \left( r\vec{r} \frac{\mathrm{d}r}{\mathrm{d}t} - r^2 \frac{\mathrm{d}\vec{r}}{\mathrm{d}t} \right) \\ &= \frac{\mathrm{d}}{\mathrm{d}t} \left(\vec{v}\times \vec{h} \right) - \mu \frac{\mathrm{d}}{\mathrm{d}t} \left(\frac{\vec{r}}{r} \right) \\ &= \mu \frac{\mathrm{d}}{\mathrm{d}t} \left( \frac{\vec{v}\times \vec{h}}{\mu} - \frac{\vec{r}}{r} \right) \end{aligned} $$上式最后一行将 $\mu$ 放到括号外,括号内部为无量纲矢量且导数为 $\vec{0}$。因此该矢量也是守恒量,记为 $\vec{e}$,可以作为轨道惯性系的基矢 $\vec{p}_1 = \vec{e}/e$(最后的基矢可以由 $\vec{p}_2 = \vec{p}_3 \times \vec{p}_1$ 得到)。考虑位移矢量 $\vec{r}$ 与 $\vec{e}$ 的点积,有
$$ \begin{aligned} \vec{r} \cdot \vec{e} &= r e \cos\theta \\ &= \vec{r} \cdot \left( \frac{\vec{v}\times \vec{h}}{\mu} - \frac{\vec{r}}{r} \right) \\ &= \frac{\vec{h} \cdot \left(\vec{r}\times \vec{v}\right)}{\mu} - \frac{\vec{r} \cdot \vec{r}}{r} \\ &= \frac{h^2}{\mu} - r \\ &= p - r \end{aligned} $$其中 $p = h^2/\mu$,解得
$$ r = \frac{p}{1+e\cos\theta} $$这正是椭圆的表达式,且 $e = |\vec{e}|$ 为离心率,$\theta$ 称为真近点角。因此:行星的轨道是以太阳为一个焦点的椭圆轨道。这就是开普勒第一定律。
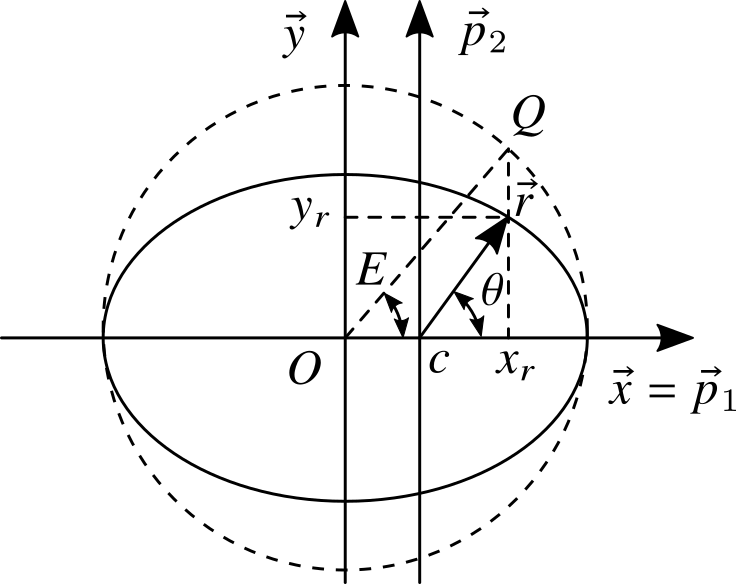
在椭圆的近拱点,速度与位置垂直,可知离心率矢量 $\vec{e}$ 的方向与半长轴方向相同。在椭圆中心建立如下图所示的 $\vec{x}$-$\vec{y}$ 平面参考系,当 $\theta = \pi/2$ 时,带入坐标 $[c,p]^\mathrm{T}$ 到椭圆方程,有
结合椭圆面积的计算公式和前面推导的 $\dot{A} = h/2$,积分一周得到运动周期为
$$ A = \pi ab = \frac{h}{2} T \quad \Rightarrow \quad T = 2\pi \sqrt{\frac{a^3}{\mu}} $$于是可以验证开普勒第三定律:行星绕太阳运动周期的平方与其半长轴的三次方成比例。
至此,我们从牛顿方程推导了开普勒运动定律。
开普勒方程
开普勒运动定律揭示了行星运动是以中心天体为焦点的椭圆,且角动量和离心率守恒决定了轨道平面的方向和椭圆的形状。只有真近点角 $\theta$ 是时间的变量,用于唯一地确定行星的位置。考察轨道参考系内,行星的位置坐标可以分解为
$$ \bm{r}^p = r \begin{bmatrix} \cos\theta \\ \sin\theta \\ 0 \end{bmatrix} $$因此有
$$ \bm{v}^p = \dot{\bm{r}}_p = \dot{r} \begin{bmatrix} \cos\theta \\ \sin\theta \\ 0 \end{bmatrix} + r \dot{\theta} \begin{bmatrix} -\sin\theta \\ \cos\theta \\ 0 \end{bmatrix} $$带入角动量守恒
$$ \bm{h}^p = \bm{r}^p \times \bm{v}^p = \begin{bmatrix} 0 \\ 0 \\ h \end{bmatrix} $$得
$$ r^2 \dot{\theta} = h \quad \Rightarrow \quad \dot{\theta} = \frac{h}{r^2} = \sqrt{\frac{\mu}{p^3}} \left(1+e\cos\theta\right)^2 $$这是一个非线性微分方程,求解比较复杂。为此,如上图,构造与椭圆中心重合且半径为 $a$ 的圆,矢量 $\vec{r}$ 在 $\vec{y}$ 方向投影的延长线与圆相交于 $Q$ 点。记 $\overrightarrow{OQ}$ 与 $\vec{x}$ 的夹角为 $E$。
考察 $\vec{r}$ 在 $\vec{x}$ 方向的投影,有
$$ r \cos\theta = a\cos E - c = a (\cos E -e) $$根据几何关系,将 $[a\cos E, r \sin\theta]^\mathrm{T}$ 代入 $\vec{x}$-$\vec{y}$ 平面内椭圆方程,有
$$ \cos^2 E + \frac{r^2 \sin^2 E}{b^2} = 1 \quad \Rightarrow \quad r\sin\theta = b \sin E = a \sqrt{1-e^2} \sin E $$将上面两个等式代入 $\bm{r}^p$ 中,可以得到用角度 $E$ 表述的坐标:
$$ \bm{r}^p = a \begin{bmatrix} (\cos E -e) \\ \sqrt{1-e^2} \sin E \\ 0 \end{bmatrix} $$因此
$$ \bm{v}^p = \dot{\bm{r}}_p = a \dot{E} \begin{bmatrix} -\sin E \\ \sqrt{1-e^2} \cos E \\ 0 \end{bmatrix} $$代入 $\bm{h}^p = \bm{r}^p \times \bm{v}^p$,整理可得
$$ \dot{E} \left( 1-e\cos E\right) = \frac{h}{a^2\sqrt{1-e^2}} = \sqrt{\frac{\mu}{a^3}} := \omega_0 $$这个微分方程称为开普勒方程。两边积分可得
$$ E(t) - e \sin E(t) = \omega_o t + E_0 $$如此做,将原本关于 $\theta(t)$ 的非线性微分方程转化为了关于 $E(t)$ 的非线性方程,避免了数值积分的累计误差。为了求解该方程,可以利用不动点法或牛顿迭代等数值解法以满足所需的精度。
参考文献
- E. Canuto, C. Novara, D. Carlucci, C.P. Montenegro, L. Massotti, Spacecraft Dynamics and Control: The Embedded Model Control Approach, Butterworth-Heinemann, 2018.