模型预测控制简介
最近在 DR_CAN 的视频中学到了模型预测控制,于是打算写篇博客记记笔记,权当公式推导的练习。
基本原理
之前在 状态反馈 里简单介绍了 LQR 设计法,这是一种最优设计,旨在使控制命令与误差的"功率"加权之和最小。然而,实际系统在扰动的影响下无法按照我们期望的那样运行,也就说外扰打破了理想的最优状态。为了解决这个问题,我们可以使用一个"滑动的窗口",在这个窗口内进行类似 LQR 的最优设计,这便是 MPC 的基本思路。
如下图所示,上面的绿色曲线表示被控对象的输出,蓝色曲线为参考信号;下面的橙色曲线为相应施加的控制信号。在数字控制中,被控对象的输出和控制器的控制命令都被离散化,样本值如散点所示。
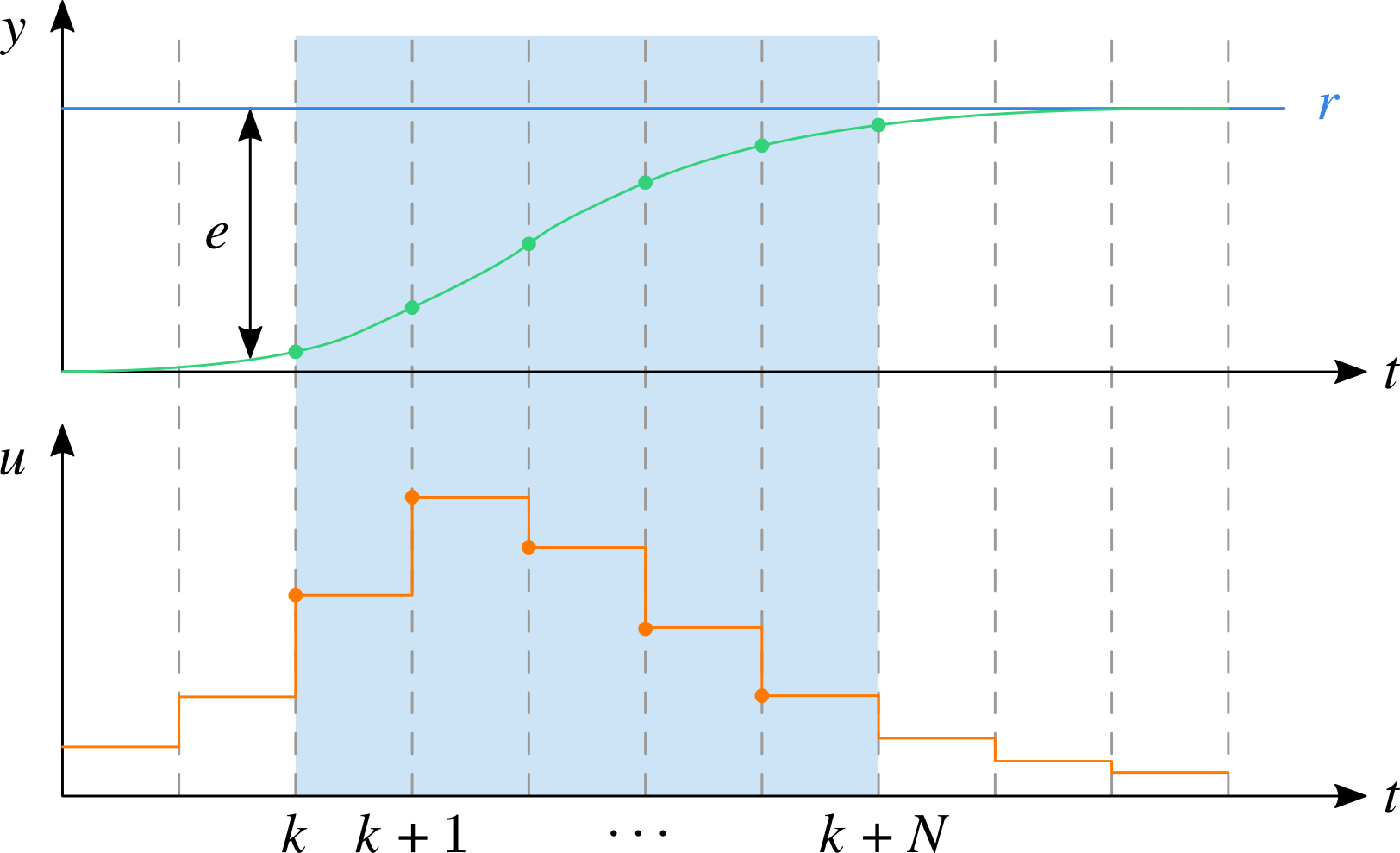
在 $k$ 时刻,模型预测控制根据当前被控对象的输出对后面的 $N$ 步进行预测,在将来的 $N$ 步内,要求控制命令和误差的平方加权和最小。即:寻找 $N$ 步控制命令($u(i),\, i=k,\,k+1,\,\dots,\,k+N-1$ ),使得下面的代价函数达到最小值
$$ J = \sum_{i=0}^{N-1} \left( e^\mathrm{T}(k+i|k) Q e(k+i|k) + u^\mathrm{T}(k+i|k) R u(k+i|k) \right) + e^\mathrm{T}(k+N|k) F e(k+N|k) $$式中,使用 $(k+i|k)$ 表示 $k$ 时刻对 $k+i$ 时刻的预测值。 $Q$ 和 $R$ 分别误差和控制的加权矩阵。应当注意的是,预测的状态比控制命令多一个右端边界的点,因此多一个端值误差的加权矩阵 $F$ 。
求解该优化问题即可得到后 $N$ 步的控制命令,但是 MPC 只施加当前时刻的命令 $u(k)$ ,下一时刻的控制命令将重复上述操作重新进行优化估计。所以说 MPC 可以认为是基于"滑动窗口"的最优设计。
上述优化问题的解决方案是使用二次规划,因此后面的推导旨在将代价函数写成如下二次规划的标准形式
$$\min_x \left( \frac{1}{2} x^\mathrm{T}Hx + f^\mathrm{T}x \right)$$公式推导
本文只介绍 MPC 的基本原理,并做如下假设
- 假设系统将输出所有状态,即 $y=x$ ;
- 假设参考信号恒为零(调节器设计),即 $r=0$ ,则有 $e=y-r=x$ 。
于是代价函数可以写作
$$ J = \sum_{i=0}^{N-1} \left( x^\mathrm{T}(k+i|k) Q x(k+i|k) + u^\mathrm{T}(k+i|k) R u(k+i|k) \right) + x^\mathrm{T}(k+N|k) F x(k+N|k) $$设系统的离散状态空间方程为
$$x(k+1) = A x(k) + B u(k)$$于是在预测的控制命令下,系统状态的预测值为
$$ \begin{aligned} x(k|k) &= x(k) \\ x(k+1|k) &= A x(k|k) + B u(k|k) = A x(k) + B u(k|k) \\ x(k+2|k) &= A x(k+1|k) + B u(k+1|k) = A^2 x(k) + AB u(k|k) + B u(k+1|k)\\ &\vdots \\ x(k+N|k) &= A^N x(k) + \sum_{i=0}^{N-1} A^{N-1-i}B u(k+i|k) \end{aligned} $$用矩阵可以将上述 $N+1$ 个方程表示为
$$ \underbrace{\begin{bmatrix} x(k|k) \\ x(k+1|k) \\ \vdots \\ x(k+N|k) \end{bmatrix}}_{\bm{X}(k)} = \underbrace{\begin{bmatrix} I \\ A \\ A^2 \\ \vdots \\ A^N \end{bmatrix}}_{M} x(k) + \underbrace{\begin{bmatrix} 0 & 0 & 0 & \cdots & 0 \\ B & 0 & 0 & \cdots & 0 \\ AB & B & 0 & \cdots & 0 \\ \vdots & \vdots & \vdots & \ddots & 0 \\ A^{N-1}B & A^{N-2}B & A^{N-3}B & \cdots & B \end{bmatrix}}_{C} \underbrace{\begin{bmatrix} u(k|k) \\ u(k+1|k) \\ \vdots \\ u(k+N-1|k) \end{bmatrix}}_{\bm{U}(k)} $$即有 $\bm{X}(k) = Mx(k) + C\bm{U}(k)$。如此做,代价函数可以表示为
$$ \begin{aligned} J &= \begin{bmatrix} x(k|k) \\ x(k+1|k) \\ \vdots \\ x(k+N|k) \end{bmatrix}^\mathrm{T} \underbrace{\begin{bmatrix} Q & 0 & \cdots & 0 & 0\\ 0 & Q & \cdots & 0 & 0\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & Q & 0\\ 0 & 0 & \cdots & 0 & F\\ \end{bmatrix}}_{\bar{Q}} \begin{bmatrix} x(k|k) \\ x(k+1|k) \\ \vdots \\ x(k+N|k) \end{bmatrix} + \begin{bmatrix} u(k|k) \\ u(k+1|k) \\ \vdots \\ u(k+N-1|k) \end{bmatrix}^\mathrm{T} \underbrace{\begin{bmatrix} R & 0 & 0 & \cdots & 0\\ 0 & R & 0 & \cdots & 0\\ 0 & 0 & R & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & R \end{bmatrix}}_{\bar{R}} \begin{bmatrix} u(k|k) \\ u(k+1|k) \\ \vdots \\ u(k+N-1|k) \end{bmatrix} \\ &= \bm{X}^\mathrm{T}(k) \bar{Q} \bm{X}(k) + \bm{U}^\mathrm{T}(k)\bar{R}\bm{U}(k) \\ &= \left(Mx(k) + C\bm{U}(k)\right)^\mathrm{T} \bar{Q} \left(Mx(k) + C\bm{U}(k)\right) + \bm{U}^\mathrm{T}(k)\bar{R}\bm{U}(k) \\ &= x^\mathrm{T}(k) M^\mathrm{T} \bar{Q} M x(k) + x^\mathrm{T}(k) M^\mathrm{T} \bar{Q} C \bm{U}(k) + \bm{U}^\mathrm{T}(k) C^\mathrm{T} \bar{Q} M x(k) + \bm{U}^\mathrm{T}(k) C^\mathrm{T} \bar{Q} C \bm{U}(k) + \bm{U}^\mathrm{T}(k) \bar{R}\bm{U}(k) \\ &= \bm{U}^\mathrm{T}(k) \underbrace{\left(C^\mathrm{T} \bar{Q} C + \bar{R}\right)}_{H} \bm{U}(k) + 2 \underbrace{x^\mathrm{T}(k) M^\mathrm{T} \bar{Q} C }_{f^\mathrm{T}} \bm{U}(k) + x^\mathrm{T}(k) M^\mathrm{T} \bar{Q} M x(k) \end{aligned} $$优化的对象为 $\bm{U}(k)$ 。注意代价函数的最后一项 $x^\mathrm{T}(k) M^\mathrm{T} \bar{Q} M x(k)$ 为常数,不影响优化结果,可以不做考虑。与二次规划的标准形式相比,代价函数存在二倍关系,应当注意 $H$ 和 $f^\mathrm{T}$ 的选择。最后使用 MATLAB quadprog 进行优化计算即可获得 $\bm{U}(k)$ 。
我在 GitHub 上传了一个简单的 MPC 例子,欢迎留言、讨论。
参考文献
- DR_CAN, 【MPC模型预测控制器】1_最优化控制和基本概念.
- DR_CAN, 【MPC模型预测控制器】2_最优化数学建模推导.