现代控制理论（5）：参考信号的引入

调节器只能将系统的各状态拉回到零位，而控制系统的根本目的是使被控对象的输出跟随参考信号，因此在调节器设计完成的基础上，还需要正确地引入参考信号。本文介绍三种常用的方式将参考信号引入到控制系统。

输入的一般形式

设被控对象的状态空间方程为

$$ \left\{ \begin{aligned} \dot{\bm{x}} &= A \bm{x} + Bu \\ y &= C \bm{x} \end{aligned} \right. $$

在实际的数字控制系统中，能够人为干涉的是状态的估计和控制律，因此，不失一般性地可以设参考信号 $r$ 的引入方式为

$$ \left\{ \begin{aligned} \dot{\hat{\bm{x}}} &= \left( {{A} - {LC} - {BK}} \right) \hat{\bm x} + {L}y + {M}r \\ u &= - K {\hat{\bm x}} + Nr \end{aligned} \right. $$

参数 $M$ 和 $N$ 的设计方法可分为如下三种情况。

标准形式 (Standard Case)

从状态观测器的角度来考察，不希望参考信号的引入对状态估计产生影响，考察状态估计的误差为

$$ \begin{aligned}\dot{\tilde{\bm{x}}} &= {A\bm{x}} + {B}\left( { - K{\hat{\bm x}} + Nr} \right) - \left[ {\left( {{A} - {LC} - {BK}} \right){\bm{\hat x}} + {L}y + {M}r} \right] \\ &= \left( {{A} - {LC}} \right){\bm{\tilde x}} + \left( {{B}N - {M}} \right)r\end{aligned} $$

因此，通过补充约束条件： $M = BN$，即可避免参考信号对状态估计引入任何扰动。此时控制器的状态空间可以进一步改写为

$$ \left\{ \begin{aligned} \bm{\dot{\hat x}} &= \left( {{A} - {LC}} \right){\bm{\hat x}} + {B}u + {L}y \\ u &= - K{\hat{\bm x}} + Nr \end{aligned} \right. $$

这就意味着状态观测器的输入与被控对象完全一致。这时，只需要对参考信号的增益 $N$ 进行设计，设计的原则是令 $r\rightarrow y$ 的增益为 $1$ 即可。考察闭环系统的状态空间

$$ \left\{ \begin{aligned} \begin{bmatrix} {{\bm{\dot{x}}}}\\ {{\bm{\dot{\tilde x}}}} \end{bmatrix} &= \begin{bmatrix} {{A} - {BK}}&{{BK}}\\ {0}&{{A} - {LC}} \end{bmatrix}\begin{bmatrix} {\bm{x}}\\ {{\bm{\tilde x}}} \end{bmatrix}+ \begin{bmatrix} {B}\\ {0} \end{bmatrix}Nr \\ y &= \begin{bmatrix} {C}&0 \end{bmatrix} \begin{bmatrix} {\bm{x}}\\ {{\bm{\tilde x}}} \end{bmatrix} \end{aligned} \right. $$

根据 $r\rightarrow y$ 的增益为 $1$ 解得

$$ N = - \left\{ \begin{bmatrix} {C}&0 \end{bmatrix} \begin{bmatrix} A - BK &BK\\ {0}&A - LC \end{bmatrix}^{-1} \begin{bmatrix} {B}\\ {0} \end{bmatrix} \right\}^{ - 1} $$

这时整个系统的框图如下图所示。

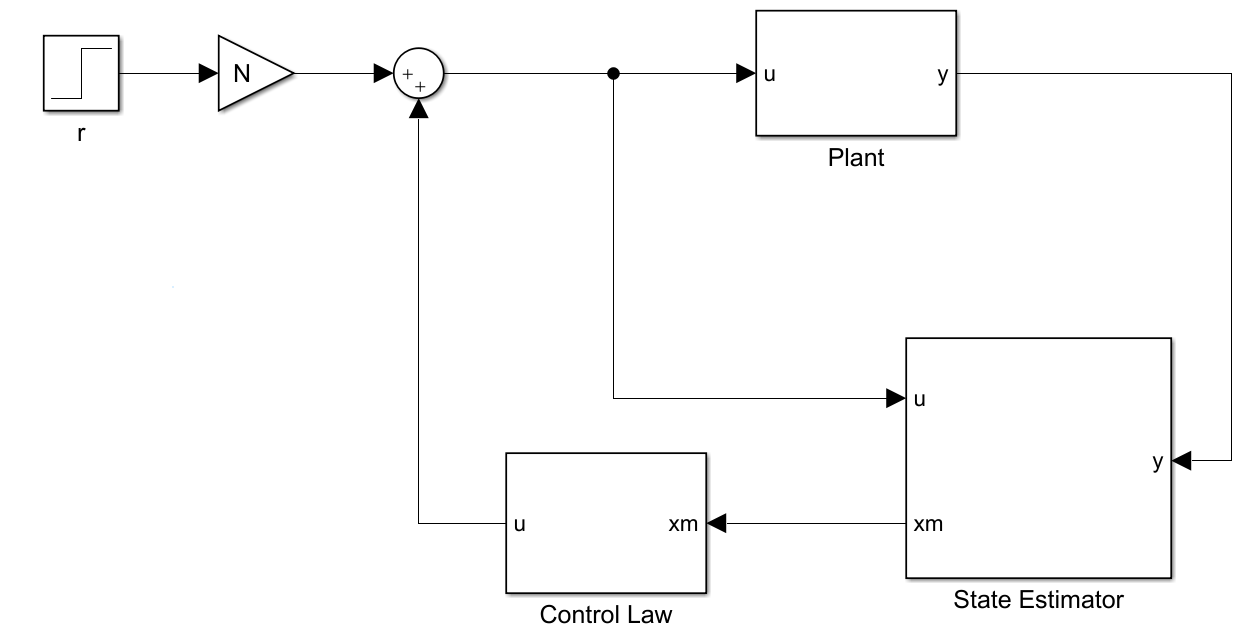
误差控制 (Error Control Case)

如果令 $N=0$ ， $M = -L$，即可得到基于误差控制的参考信号引入方式，这是经典控制中的常用方式，如下图所示。

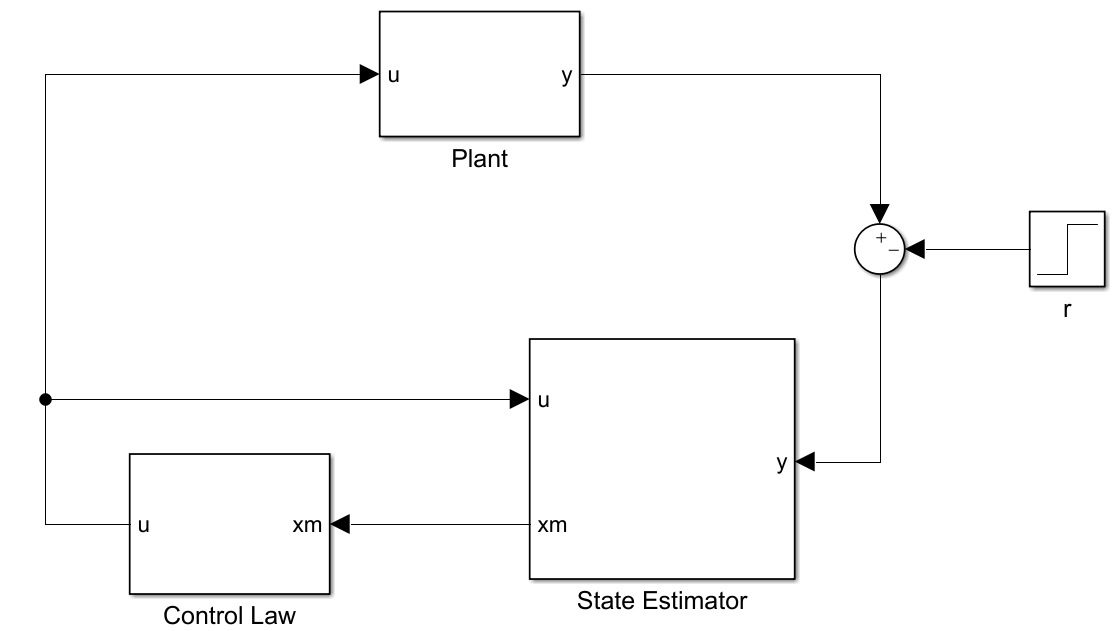
这种简单的方式可以用传递函数来证明其可靠性，设开环传递函数为 $H_{\rm open}$，则 $r\rightarrow y$ 的传递函数即为闭环传递函数

$$H_{close}=\frac{H_{\rm open}}{1+H_{\rm open}} \rightarrow 1$$

应当注意，上式成立的条件是 $H_{\rm open}$ 在带宽内具有足够的增益，这通常要求开环传递函数中存在一个或多个 $\frac{1}{s}$ 项，若被控对象本身无法满足这一条件，可考虑在控制器中增加积分环节。

一般形式 (General Case)

更一般地，可以通过人为设计参数 $M$ 和 $N$ 来设计 $r\rightarrow u$ 的零点从而改变 $r\rightarrow y$ 的零点以改善系统的动态特性。$r\rightarrow u$ 的零点满足（这里关注 $r$ ，可以暂时令 $y=0$ ）

$$ \begin{gathered} \begin{vmatrix} {{I}s - \left( {{A} - {BK} - {LC}} \right)}&{ - {M}} \\ { - {K}}&N \end{vmatrix} = 0 \\ \Downarrow \\ \left| {{I}s - {A} + {BK} + {LC} - \frac{{M}}{N}{K}} \right| = \left| {{I}s - {A} + {BK} + {LC} - {{\bar MK}}} \right| = 0 \end{gathered} $$

因此，我们可以首先根据零点对进行 ${\bar{M}}=\frac{M}{N}$ 设计，再根据 $r\rightarrow y$ 的增益为 $1$ 计算得 $N$ 。这种方式的系统框图如下图所示。

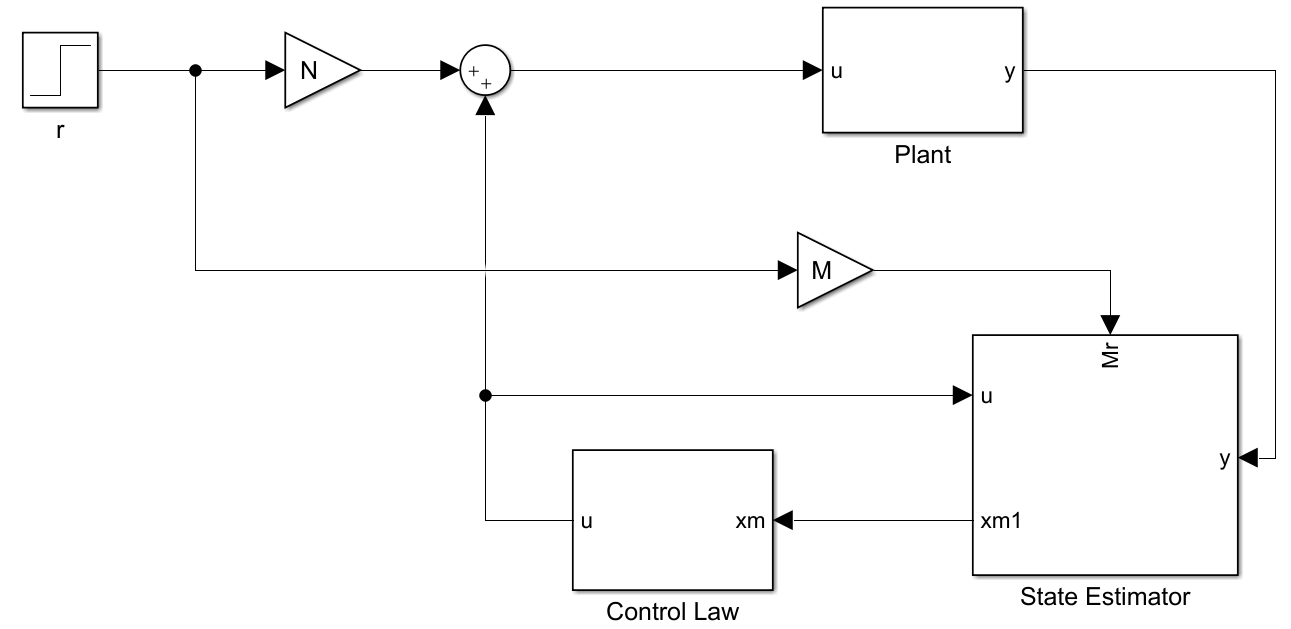
参考文献

1. G.F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. 2014.