状态估计器提供了状态的估计值,在分离原理的指导下,利用估计的状态进行状态反馈能够使系统稳定。本文讨论最基本的闭环设计,即调节器设计。
状态反馈指出可以利用系统的状态变量的线性组合 u = − K x u=-K\bm{x} u = − K x u = − K x ^ u=-K\hat{\bm{x}} u = − K x ^
设被控对象的状态空间表述为
{ x ˙ = A x + B u y = C x
\left\{
\begin{aligned}
\dot{\bm{x}} &= A \bm{x} + Bu \\
y &= C \bm{x}
\end{aligned}
\right.
{ x ˙ y = A x + B u = C x 相应构建状态估计器为
x ^ ˙ = A x ^ + B u + L ( y − C x ^ ) \dot{\hat{\bm{x}}} = A\hat{\bm{x}}+Bu+L\left(y-C\hat{\bm{x}}\right) x ^ ˙ = A x ^ + B u + L ( y − C x ^ ) 则状态误差 x ~ = x ^ − x \tilde{\bm{x}}=\hat{\bm{x}}-\bm{x} x ~ = x ^ − x
x ~ ˙ = ( A − L C ) x ~ \dot{\tilde{\bm{x}}}=\left(A-LC\right)\tilde{\bm{x}} x ~ ˙ = ( A − L C ) x ~ 控制律为
u = − K x ^ = − K ( x ~ + x ) u=-K\hat{\bm{x}}=-K\left( \tilde{\bm{x}} + \bm{x} \right) u = − K x ^ = − K ( x ~ + x ) 综上,整个闭环系统的状态空间可表述为:
[ x ˙ x ~ ˙ ] = [ A − B K − B K 0 A − L C ] [ x x ~ ]
\begin{bmatrix}
\dot{\bm{x}} \\
\dot{\tilde{\bm{x}}}
\end{bmatrix} =
\begin{bmatrix}
{A} - {BK} & - {BK} \\
0 & {A} - {LC}
\end{bmatrix}
\begin{bmatrix}
{\bm{x}} \\
\bm{\tilde x}
\end{bmatrix}
[ x ˙ x ~ ˙ ] = [ A − B K 0 − B K A − L C ] [ x x ~ ] 闭环的系统矩阵为上三角矩阵,其特征值为 A − B K A-BK A − B K A − L C A-LC A − L C
根据分离原理,进行闭环设计时可以分别对控制器和状态观测器进行设计,然后将控制器所用的状态量替换为状态估计器输出的状态估计值即可。
设一负弹簧系统的特征角频率为 ω n = 2 r a d / s \omega_n = 2 \,\rm{rad/s} ω n = 2 rad/s
{ x ˙ = [ 0 1 ω n 2 0 ] x + [ 0 1 ] u y = [ 1 0 ] x
\left\{ \begin{aligned}
\bm{\dot x} = \begin{bmatrix}
0&1\\
{\omega _n^2}&0
\end{bmatrix}{\bm{x}} + \begin{bmatrix}
0\\
1
\end{bmatrix} u \\
y = \begin{bmatrix}
1&0
\end{bmatrix}{\bm{x}}
\end{aligned} \right.
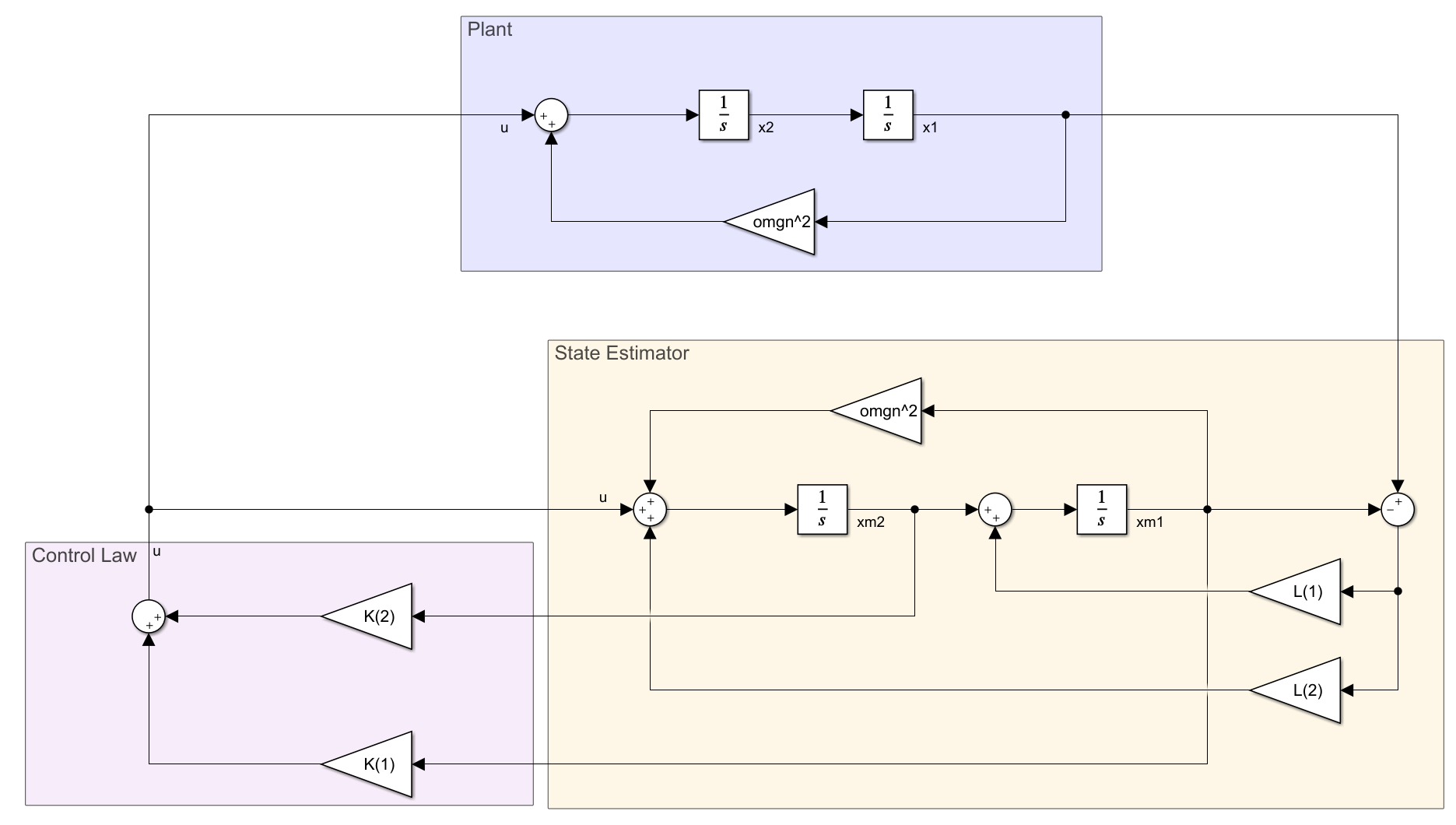
⎩ ⎨ ⎧ x ˙ = [ 0 ω n 2 1 0 ] x + [ 0 1 ] u y = [ 1 0 ] x 仿真模型如下图所示,紫色区域为被控对象(Plant),其输入为控制器的输出信号 u u u u u u y = x 1 y=x_1 y = x 1 L L L K K K u u u
被控对象与控制器仿真模型
为了稳定系统,可将控制器的极点布置在 − 0.5 ± 0.866 j -0.5\pm0.866j − 0.5 ± 0.866 j − 3.5 ± 3.571 j -3.5\pm3.571j − 3.5 ± 3.571 j place 函数实现,如
% Plant
omgn = 2 ;
A = [ 0 1 ; omgn ^2 0 ];
B = [ 0 1 ] ' ;
C = [ 1 0 ];
% Control Law
K = place ( A , B ,[ - 0.5 + 0.866 j - 0.5 - 0.866 j ]);
% State Estimator
L = place ( A ' , C ' ,[ - 3.5 + 3.571 j - 3.5 - 3.571 j ]);
L = L ' ;
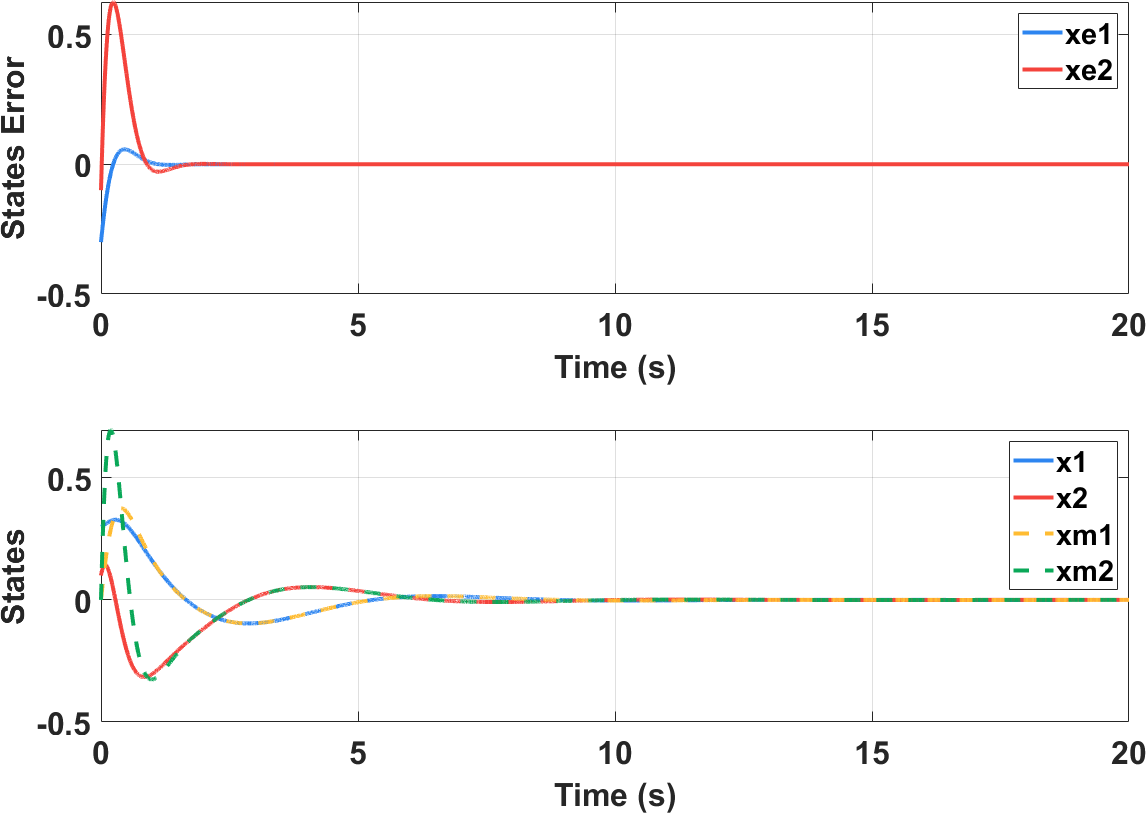
参数设计完成后带入仿真,运行后结果如下图所示。由于设计了被控对象初始状态非零,因而初期存在状态误差,该误差收状态估计器调节而收敛。系统的状态和估计受到控制律约束,克服负刚度造成的不稳定影响,最终各状态稳定到零位。对比两图可见,状态估计器的带宽大于控制器的带宽,因而状态误差的收敛比状态的收敛更快。
调节器仿真结果
G.F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. 2014.