现代控制理论（3）：状态估计

现代控制讲究状态反馈，然而系统的状态不一定是直接测得的，这就需要用到本文介绍的状态估计器进行状态估计。

全维状态估计器

设线性时不变被控对象的状态空间表述为：

$$ \left\{ \begin{aligned} \dot{\bm{x}} &= A \bm{x} + Bu \\ y &= C \bm{x} \end{aligned} \right. $$

据此，构建相同的理论模型：

$$ \left\{ \begin{aligned} \dot{\hat{\bm{x}}} &= A \hat{\bm{x}} + Bu \\ \hat{y} &= C \hat{\bm{x}} \end{aligned} \right. $$

在该理论模型中，带帽子的变量（如 $\hat{x}$）表示估计值。由于是理论模型，其所有信息都可以通过计算机获得。理论模型和被控对象输入相同的 $u$ 时，原则上两者的响应相同，因而状态和输出都应当相同。然而实际上，由于被控对象和理论模型初始状态的偏差、理论模型的建模误差、被控对象的额外扰动、传感器的测量噪声等因素的影响，实际输出和理论输出并不相同，因而状态也不相同。

When in trouble, use feedback。为了解决模型之间的差异，遵循这个控制的金科玉律，对理论模型引入反馈进行矫正，令：

$$\bm{\dot{\hat{x}}} = A\hat{\bm{x}} + { B}u + {L}\left( {y - \hat y} \right)$$

此时状态的估计误差 ${\bm{\tilde x}} = {\bm{x}} - {\bm{\hat{x}}}$ 满足：

$$\bm{\dot{\tilde{x}}} = \left( A - LC \right) \bm{\tilde{x}}$$

于是，只要合理设计 $L$ 令 $\left( A - LC \right)$ 所有特征值的实部均小于零即可使状态估计误差收敛到零，即状态估计值趋近于真是状态。

状态估计器 $L$ 的设计与状态反馈 $K$ 的设计完全相同，考察数学关系：

$$ \left| {{A} - {LC}} \right| = \left| {{{\left( {{A} - {LC}} \right)}^T}} \right| = \left| {{{A}^T} - {{C}^T}{{L}^T}} \right| \leftarrow \left| A - BK \right| $$

即：状态观测器与控制律之间存在对偶关系，设计时只需分别将 $A$ 、 $C$ 、$L$ 转置后采用与状态反馈相同的方法进行极点配置即可。

下面给出一个全维状态估计器的例子。

设弹簧-质量-阻尼系统的状态空间为：

$$ \left\{ \begin{aligned} \dot{\bm{x}} &= \begin{bmatrix} 0 & 1 \\ -\omega_n^2 & -2\zeta \omega \end{bmatrix} \bm{x} + \begin{bmatrix} 0 \\ \omega_n^2 \end{bmatrix}u \\ y &= \begin{bmatrix} 1 & 0 \end{bmatrix}\bm{x}\ \end{aligned} \right. $$

其中，$\omega_n=1 {\rm rad/s,}\, \zeta=0.3$，基于Simulink搭建被控对象如图所示

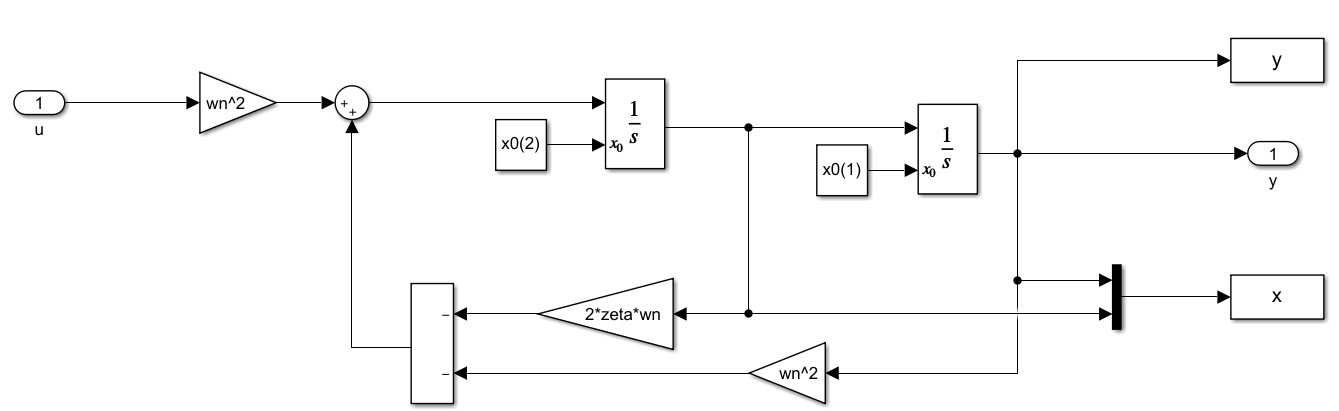
为了状态估计能够快速收敛，设的阻尼系数 $\zeta=0.7$ ，对应极点为 $-0.70\pm0.71j$ ，进而 $L=\left[0.80,, -0.48\right]$。带入仿真，观察状态的实际值和估计值如下图所示：

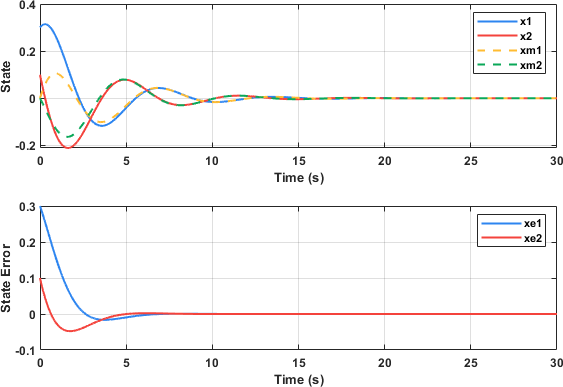
第一个子图实线为真实状态，虚线为状态估计值，可见两者在大约5s后趋于一致。第二个子图则表示两个状态的估计误差，同样可以反应状态估计值的误差随时间收敛到零，状态估计值趋于真实值。

降维状态估计器

上面介绍的状态估计器称之为全维状态估计器，因为它对系统的所有状态都进行了估计。然而，在一些情况下，系统的输出就是系统的某一个状态，能否直接利用这个状态，仅对其他状态进行估计呢？这时就需要用降维状态估计器。

以单输入单输出系统（SISO，Single Input Sigle Output）为例，将其状态空间方程拆解为：

$$ \left\{ \begin{array}{l} \begin{bmatrix} \dot{x}_a \\ \dot{\bm{x}}_b \end{bmatrix} = \begin{bmatrix} A_{aa} & A_{ab} \\ A_{ba} & A_{bb} \end{bmatrix}\begin{bmatrix} x_a \\ \bm{x}_b \end{bmatrix} +\begin{bmatrix} B_a \\B_b \end{bmatrix} u \\ y = \begin{bmatrix} 1&0 \end{bmatrix}\begin{bmatrix} x_a \\ \bm{x}_b \end{bmatrix} \end{array} \right. $$

系统的输出就是状态量 $x_a$ ，需要进行估计的状态为 $\bm{x}_b$ 。

为了实现降维，需要对原始的状态空间方程进行改造，构造新的系统，使其状态变量有且仅有 $\bm{x}_b$ 。

首先从 $\dot{\bm{x}}_b$ 的方程中寻找新的系统输入方程：

$$\dot{\bm{x}}_b = {{A}_{bb}}{{\bm{x}}_b} + \left( {{A_{ba}}{x_a} + {{ B}_b}u} \right)$$

将 $\dot{x}_a$ 换为输出的导数 $\dot{y}$ ，改写系统的输出方程：

$$\left( {\dot{y} - {A_{aa}}{x_a} - {B_a}u} \right) = {{A}_{ab}}{{\bm{x}}_b}$$

由上面两个式子，对比标准的状态空间方程，显然有以下转换关系：

$$ \left\{ \begin{array}{l} {\bf{x}} \to {{\bf{x}}_b}\\ {A} \to {{A}_{bb}}\\ {B}u \to \left( {{A_{ba}}{x_a} + {{B}_b}u} \right)\\ C \to {{A}_{ab}}\\ y \to \left( {\dot y - {A_{aa}}{x_a} - {B_a}u} \right) \end{array} \right. $$

根据全维状态估计器的设计方法，对这个转换后的"新系统"进行状态估计器设计，有

$$ \begin{aligned} \dot{\hat{\bm{x}}}_b &= {{A}_{bb}}{{{\bf{\hat x}}}_b} + \left( {{A_{ba}}{x_a} + {{B}_b}u} \right) + {{L}_b}\left[ {\left( {\dot y - {A_{aa}}{x_a} - {B_a}u} \right) - {{A}_{ab}}{{{\bf{\hat x}}}_b}} \right] \\ &= \left( {{{A}_{bb}} - {{L}_b}{{A}_{ab}}} \right){{{\bf{\hat x}}}_b} + \left( {{A_{ba}} - {{L}_b}{A_{aa}}} \right)y + \left( {{{B}_b} - {{L}_b}{B_a}} \right)u + {{L}_b}\dot y \end{aligned} $$

由此初步完成了降维估计器的构造，设计的目标只需令 $A_{bb} - L_bA_{ab}$ 的所有特征值实部为负。需要注意的是，上式中包含输出的导数 $\dot{y}$，实际中微分是不容易实现的，且容易放大高频噪声，应当避免这一项的存在。于是需要进一步构造辅助变量 $\bm{x}_c = \bm{\hat x}_b - L_by$ ，则上式改为：

$$ \dot{\hat{\bm{x}}}_c = \left( {{{A}_{bb}} - {{L}_b}{{A}_{ab}}} \right)\left( {{{\bf{x}}_c} + {{L}_b}y} \right) + \left( {{A_{ba}} - {{L}_b}{A_{aa}}} \right)y + \left( {{{B}_b} - {{L}_b}{B_a}} \right)u $$

至此，推导出降维状态估计器的可实现的形式。对于本文所提及的弹簧-质量-阻尼系统，其降维状态估计器结构如下图所示：

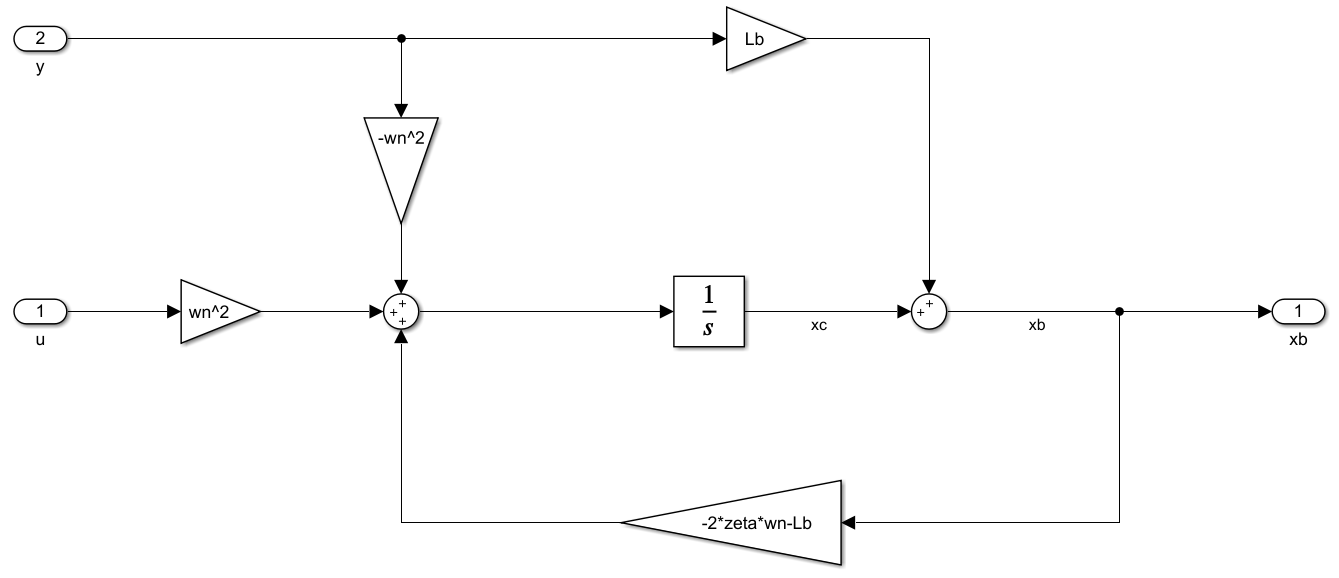
对降维状态估计器进行参数设计，之后得到该估计器的响应如图：

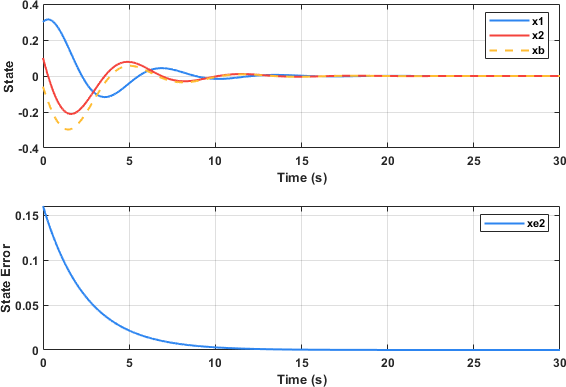
该降维状态估计器仅对状态量 $x_2$ 进行估计，可见在 8s 左右估计的误差已收敛到合适的范围，随着时间的增长，状态估计误差收敛于零，状态估计值收敛于真实值。

全维状态估计器还是降维状态估计器？这是一个开放性的问题，全维状态估计器的所有状态响应都有一定的收敛过程，而降维状态估计器利用系统输出作为已知状态，仅被估计的状态存在收敛过程，从这一方面看，降维状态估计器具有"更快"的效果；然而，降维估计器中对应于系统输出的状态容易受到传感器噪声的影响，而全维状态估计可以对噪声进行滤波，因而全维状态估计器具有"更低噪声"的效果。

参考文献

1. G.F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. 2014.