现代控制理论（2）：状态反馈

2020-07-08 2023-06-29 约 1337 字预计阅读 3 分钟

状态反馈是现代控制理论的基础，本文分析其基本原理，并介绍主导极点法和 LQR 设计法两种参数设计方法。

状态反馈的原理

现代控制理论基于状态空间建模，对于连续的线性时不变系统，其状态空间可表述为：

$$ \left\{ \begin{aligned} \dot{\bm{x}} &= A \bm{x} + Bu \\ y &= C \bm{x} + Du \end{aligned} \right. $$

通常情况下 $D=0$ 。

如果系统矩阵 $A$ 存在正实部的特征值而导致系统不稳定，或是系统虽然稳定但性能不满足需求，可以通过反馈控制来改变系统特性。现代控制理论采用的状态反馈区别于经典控制中利用输出和参考信号的误差进行反馈，其根据系统的状态来计算控制信号，对于线性系统，反馈信号可表述为 $u = -K{\bm{x}}$ ，此时系统的动态响应变为

$$\dot{\bm{x}} = \left( A-BK \right) \bm{x}$$

因此，只要我们合理设计反馈增益 $K$ ，使得 $A-BK$ 的特征值（对应传递函数的极点）均分布在复平面的左半平面，即可实现系统的稳定。

常用的系统极点的配置方法有主导极点法和 LQR 设计法，下面用一些例子来介绍反馈增益的设计方法。

主导极点法

稳定系统的收敛速度取决于离虚轴最近的极点，称为主导极点。主导极点法是将主导极点按照适当的二阶系统进行配置，引入相应的阻尼和刚度使其满足要求；对于其他的非主导极点，将其布置在实轴上，并尽可能远离主导极点，使这些极点领导的响应能够快速收敛。

设某系统状态空间矩阵为：

$$ \begin{aligned} {A} &= \begin{bmatrix} 0&2&0&0&0 \\ { - 0.1}&{ - 0.35}&{0.1}&{0.1}&{0.75} \\ 0&0&0&2&0 \\ {0.4}&{0.4}&{ - 0.4}&{ - 1.4}&0 \\ 0&{ - 0.03}&0&0&{ - 1} \end{bmatrix} \\ {B} &= \begin{bmatrix} 1&0&0&0&0 \end{bmatrix} \\ {C} &= \begin{bmatrix} 1&0&0&0&0 \end{bmatrix} \end{aligned} $$

容易计算系统矩阵的特征值有： $[0,-0.5075,-0.9683,-0.6371\pm0.6669j]$ ，可见改系统具有四个稳定的极点和一个位于原点的极点，可以判定该系统为Ⅰ型系统：系统的阶跃响应收敛于斜直线，如下图所示：

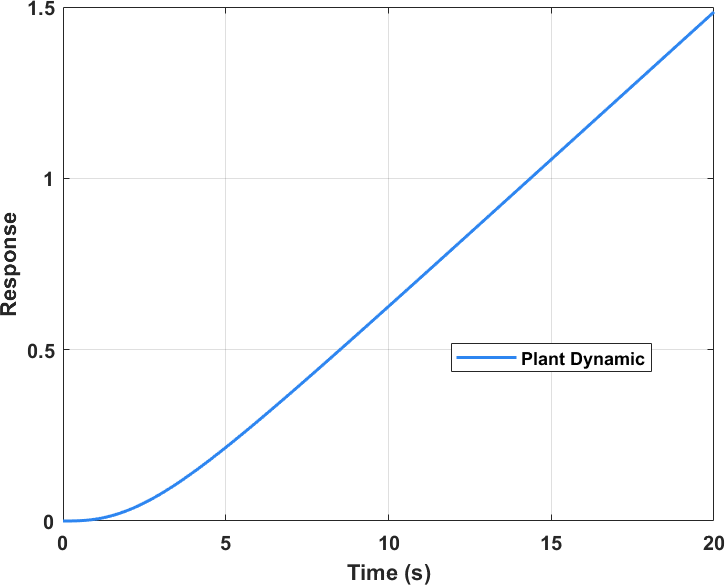
通过计算二阶系统的响应，我们发现在 $\omega_n = 1 \rm{ rad/s} , \zeta = 0.5$ 时二阶系统 $H(s)=\frac{\omega_n^2}{s^2+2\zeta\omega_ns+\omega_n^2}$ 的响应接近需求，其极点为 $-0.5\pm0.866j$ 。

因此，我们可以将该系统的主导极点设置为二阶系统的极点，其他极点的距离4倍于主导极点，设置为 $-4$ 。

在 MATLAB 中使用函数 acker 或 place 均可以实现极点配置，前者由于容易引入数值误差，一般用于阶数较低（$\le10$）的系统；后者的算法是基于特征向量来的，应当避免使用重复极点，必要时可以使重复极点具有微妙的差别。设计时应当注意极点移动的距离越大，意味着反馈增益越大，即需要的能量越大，应当充分考虑执行机的能力。

通过极点配置，反馈后系统矩阵 $A-BK$ 的特征值为：$[-0.5 \pm 0.866j,\,-3.99,\,-4,\,-4.01]$。进而可以得到系统响应为（输出按20s处的值进行了归一化以便于对比）：

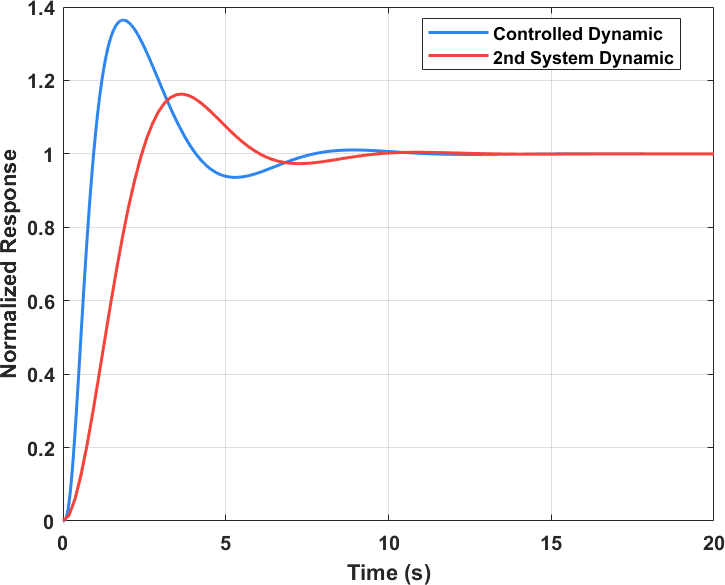
LQR设计法

LQR设计旨在寻找合适 $K$ 的使得下面的积分取得最小值

$${\mathcal{J} } = \int_0^\infty { { {\bm{x} }^T}Q{\bm{x } }+{ {\bm{u} }^T}R{\bm{u} } } \,\mathrm{d} t$$

其中， $Q$ 和 $R$ 的选取是相对"任意"的，初次设计时，可以将其选择为对角矩阵，并令各对角元素为允许误差平方的导数，即：

$${Q_{ii} } = \frac{1}{ {\max (x_i^2)} },\quad {\text{ } }{R_{ii} } = \frac{1}{ {\max (u_i^2)} }$$

选定 $Q$ 和 $R$ 后，利用MATLAB函数 lqr 即可完成设计。

这里，我们令 $R=1$ ，采用两种 $Q$ 进行设计对比，结果如下图所示

$$ \begin{aligned} {{Q}_1} &= \begin{bmatrix} {25}&0&0&0&0 \\ 0&{25}&0&0&0 \\ 0&0&{25}&0&0 \\ 0&0&0&{25}&0 \\ 0&0&0&0&{25} \end{bmatrix} \\ {{Q}_2} &= \begin{bmatrix} 4&0&0&0&0 \\ 0&{100}&0&0&0 \\ 0&0&4&0&0 \\ 0&0&0&{100}&0 \\ 0&0&0&0&4 \end{bmatrix} \end{aligned} $$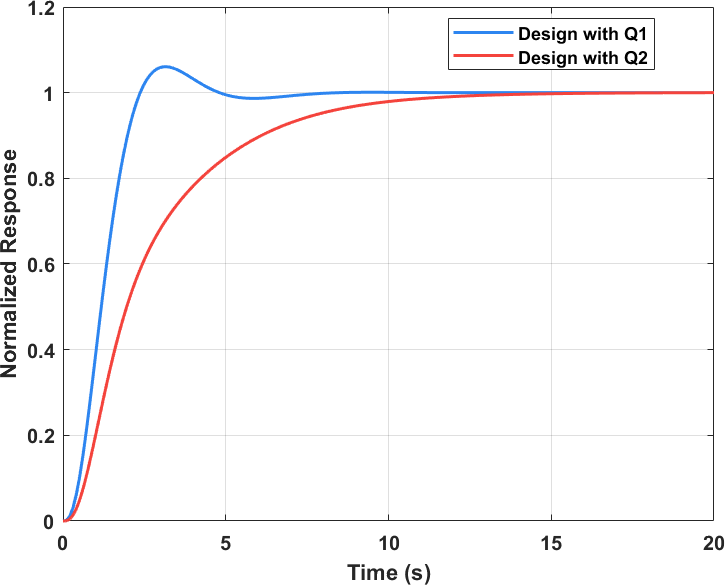

下面给出参数设计的部分源码以供参考，本文所述工作已整理在控制理论学习仓库，欢迎讨论！

matlab

% Plant
A = [0 2 0 0 0; -0.1 -0.35 0.1 0.1 0.75; 0 0 0 2 0;
     0.4 0.4 -0.4 -1.4 0; 0 -0.03 0 0 -1];
B = [0 0 0 0 1]';
C = [1 0 0 0 0];

% Dominant Second-Order Poles
p = [-0.5+0.866i -0.5-0.866i -3.99 -4.00 -4.01]';
K = place(A,B,p);

% Linear Quadratic Regulator
xm = [0.2 0.2 0.2 0.2 0.2];
Q = diag(1./xm.^2)
R = 1;
K = lqr(A,B,Q,R);

参考文献

G.F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. 2014.

目录

现代控制理论（2）：状态反馈

状态反馈的原理

主导极点法

LQR设计法

参考文献