LPSD 功率谱估计
欧洲航空局(ESA)为LISA计划设计了完整的数据处理工具包 LTPDA,该工具包中内置一种对数频率点功率谱估计算法,即 LPSD 算法。本文介绍该算法的基本原理,并基于 MATLAB 进行复现。
背景:常用功率谱估计算法
功率谱估计是频域分析的一种常用手段,可用来检测信号中的单频信号或评估仪器的噪声本底等。常用的功率谱估计算法有周期图法(对应 MATLAB 函数为 periodogram)和 Welch 方法(pwelch)。对于采集系统收集到的数字信号,周期图法会对该数据进行加窗,然后利用快速傅里叶变换(FFT)将信号转化到频域
然后利用 Wiener–Khinchin 定理即可获得功率谱
$$ S(k) = \frac{2}{Nf_s}|X(k)|^2 $$式中,系数 $2$ 将双边谱转换到单边谱,这是因为负频率不具备实际的物理意义。
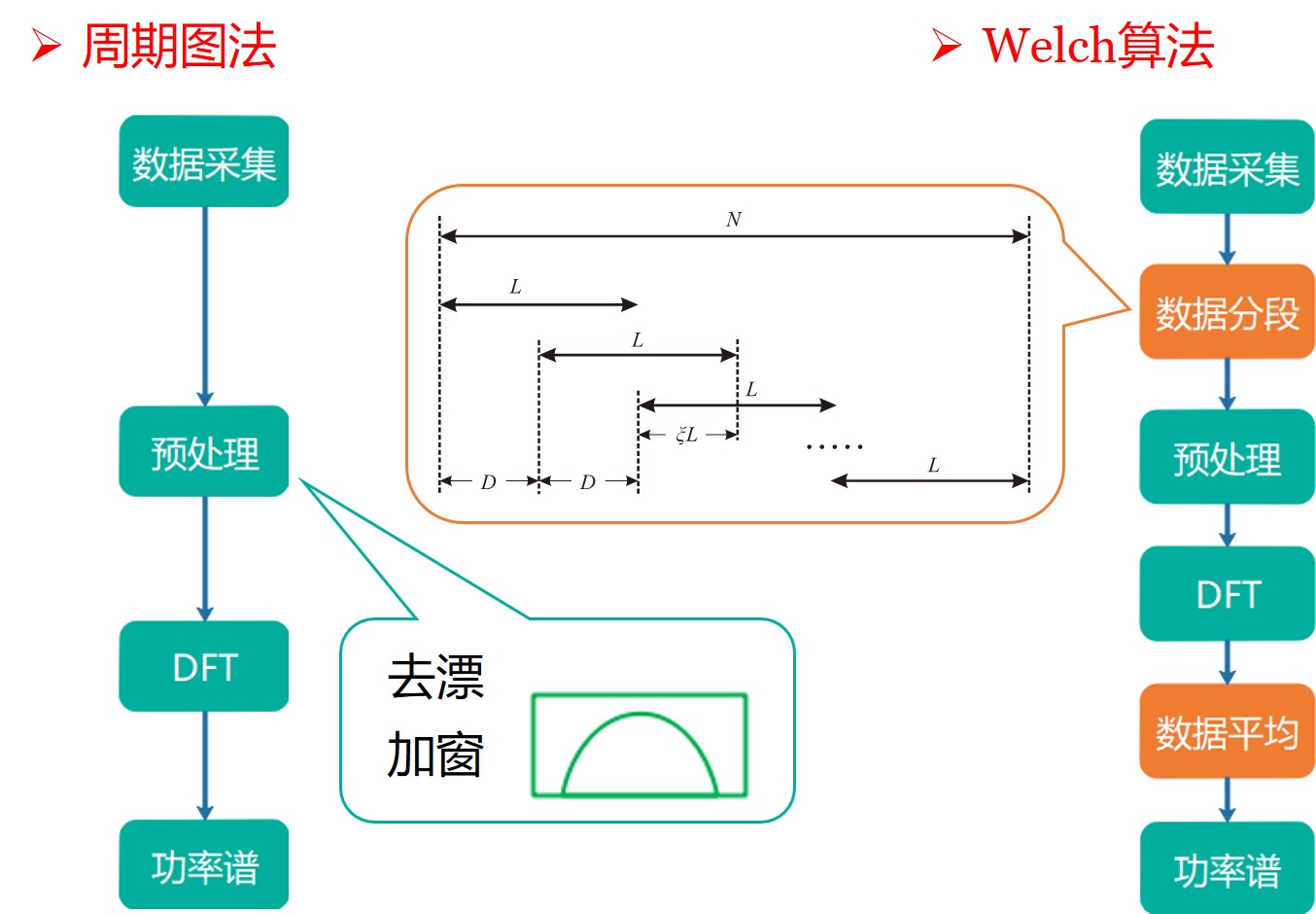
Welch 方法相对于周期图法增加了分段平均的思想,其将数据等分为多段,并且允许各段数据之间具有一定的重叠率以补偿窗函数引入的数据不平权的影响。对每段数据采用周期图法,最后将各段分别计算的功率谱进算数平均,获得最终的谱估计值。
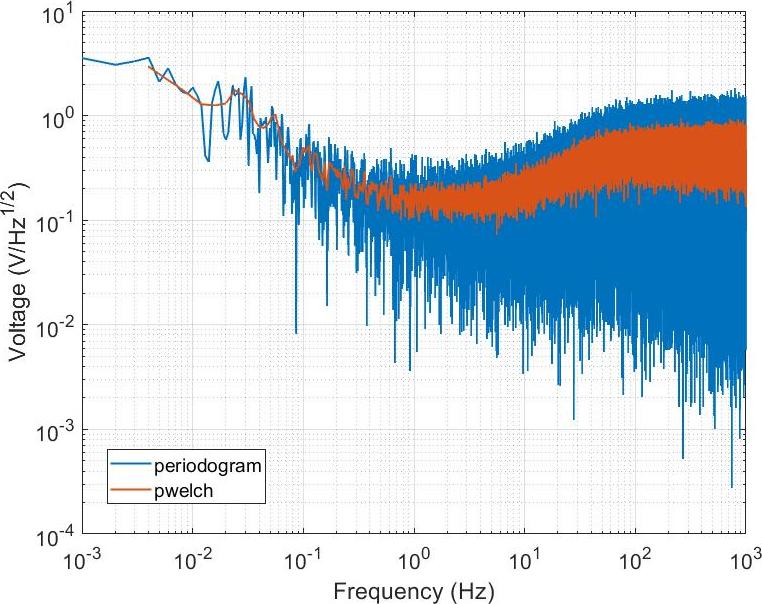
上图展示了周期图法和 Welch 方法对功率谱估计的结果。其中,蓝色曲线的周期图法一次性使用了全部的数据,因而有最高的频率分辨率,可以看到更低的频带。但是其高频部分的数据波动较大,且波动范围不会随着点数的增加而减小,即不满足所谓的一致性原则。橙色的 Welch 算法由于对数据进行了分段,直接进行 FFT 的数据相对较少,导致频率分辨率降低。但是分段平均使得高频波动的幅值大大减小,可以验证高频波动会随着分段次数的增加而进一步减小。
LPSD算法
LPSD 算法的基本思想是采用对数分布的频率点,由于此时频率点的差值不是定值,即 DFT 的频率分辨率随频率点变化,因而在求取每个频率点对应的功率谱密度时应当对原始数据进行不同的分段。这就是说,LPSD 算法的每个频率点对应于不同分段次数下 Welch 算法中的相应点。
对数频率的选取
记采集到的离散数据为 $x(n),n=0,1,2…N-1$,采样率为 $f_s$。假设希望计算 $J_{\rm des}$ 个点,其中第 $j$ 个点对应的频率为 $f(j)$、功率谱密度为 $P(j)$ 、频率分辨率为 $r(j)=f(j+1)-f(j)$。应当注意的是,这里的频率分辨率是指计算DFT的频率点之间的间隔,更一般的说法应当是栅栏效应。有限长数据的频率分辨率实际由 DTFT 定义,与数据的时间长度互为倒数,本文中称之为最小分辨率 $r_{\rm min}$。在 LPSD 算法中不能采用 logspace 生成对数分布的频率点,因为数值计算的频率间隔不应当小于最小分辨率,否则这种计算是没有意义的。
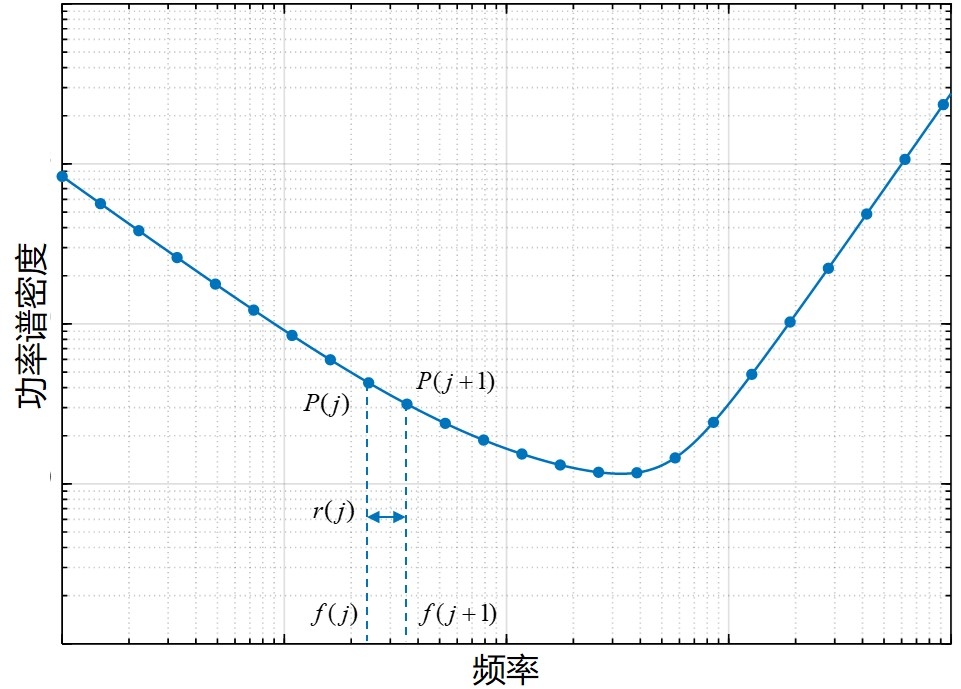
为了计算频率点,首先考察严格对数均匀的频率点应当满足
$$\log f(j + 1) - \log f(j) = C$$其中C为常数。频率范围受分辨率和采样率的影响,取
$$ \begin{gathered} f(1) = {r_{\rm min}} = \frac{{{f_s}}}{N} \\ f({J_{\rm des}}) = {f_{\rm max}} = \frac{{{f_s}}}{2} \end{gathered} $$再令
$$g=\log f_{\rm max}- \log r_{\rm min}=\log \frac{N}{2}$$可以得到第 $j$ 个点的频率和频率分辨率分别为
$$ \begin{gathered} f(j) = {r_{\rm min}} \times {10^{\frac{{j - 1}}{{{J_{\rm des}} - 1}}g}} \\ {r_0}(j) = f(j)({10^{\frac{g}{{{J_{\rm des}} - 1}}}} - 1) \end{gathered} $$为了使低频段到高频段的频率分辨率变化较连续,对中频段对应的频率分辨率进行调整,为此,引入分段次数期望值 $K_{\rm des}$(其典型值为100)。在分段重叠率为 $\xi$ 时满足
$$({K_{\rm des}} - 1)(1 - \xi ){L_{\rm avg}} + {L_{\rm avg}} = N$$
此时对应的频率分辨率为
$$r_{\rm avg}=\frac{f_s}{L_{\rm avg}}=\frac{f_s}{N}\left[ (K_{\rm des}-1)(1-\xi) +1 \right]$$根据分辨率限制和算法需求,我们需要对频率分辨率进行调整,如下
$$ r'(j) = \left\{ \begin{array}{ll} {{r_0}(j)}& {r_0}(j) \ge {r_{\rm avg}} \\ {\sqrt {{r_0}(j) \cdot {r_{\rm avg}}} }&{r_0}(j) < {r_{\rm avg}}{\text{ and }}\sqrt {{r_0}(j) \cdot {r_{\rm avg}}} > {r_{\min }} \\ {{r_{\rm min}}}&\text{else} \end{array} \right. $$除此之外,为了保证依据频率分辨率分段的数据长度为整数,频率分辨率还应当做进一步调整
$$ \begin{gathered} L(j) = \left\lfloor {\frac{{{f_s}}}{{r'(j)}}} \right\rfloor \\ r(j) = \frac{{{f_s}}}{{L(j)}} \end{gathered} $$其中,符号 $\left\lfloor \right\rfloor$ 表示向下取整。
综上所述,对数频率的选取算法为:以 $f(1)=r_{\rm min}$ 为起点,根据频率和 $J_{\rm des}$ 求解分辨率 $r_0(j)$ ,并根据要求对分辨率进行调整,得到 $r(j)$,接着利用 $f(j+1)=f(j)+r(j)$ 进行迭代。当计算的频率达到奈奎斯特频率即可停止迭代。值得注意的是,由于对频率分辨率进行了修正,获得的频率点并不是严格的对数分布,同时也会导致实际获得的频率点 $J$ 与期望的点数 $J_{\rm des}$ 并不相等。
数据的分段处理
对于第 $j$ 个频率点,由前可知其频率分辨率为 $r(j)$,分段后的每段数据长度为 $L(j)$。为了减小窗函数导致的数据不等权,允许分段之间存在一定的重叠率 $\xi$,数据分段如下图所示。
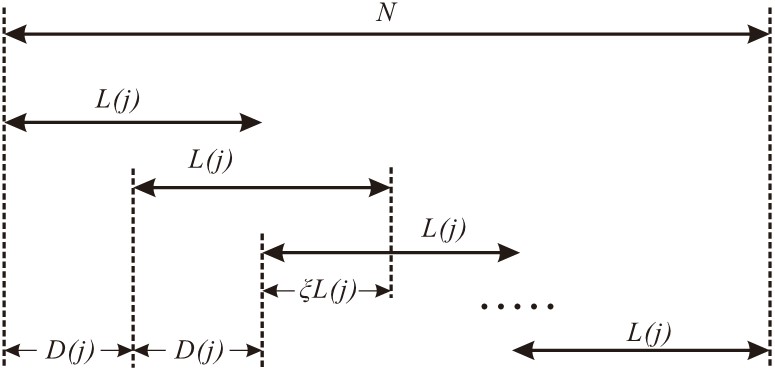
由图可知,每段数据未重叠部分长度为
$$D(j) = (1 - \xi ) \cdot L(j)$$因而分段次数为
$$K(j) = \left\lfloor {\frac{N - L(j)} {D(j) + 1} } \right\rfloor$$针对每段数据,我们可以选择利用 mean 函数求取数据平均值后予以扣除,或利用 detrend 函数直接去除数据中线性漂移。以扣除平均值为例,第 $j$ 个频率点的第 $k$
段数据平均值为
将该段数据扣除平均值后,以相同长度的窗函数 $w(j,l)$ 对数据段进行加窗,得到预处理的数据段
$$ G(j,k,l) = \left[ {x\left( {D(j) \cdot (k - 1) + l} \right) - a(j,k)} \right] \cdot w(j,l) ,\quad l = 1,\,2,\,3\,...\,L(j) $$然后对 $G(j,k,l)$ 进行离散傅里叶变换
$$A(j,k) = \sum\limits_{l = 1}^{L(j)} {G(j,k,l) \cdot {e^{ - 2\pi i\frac{m(j)}{L(j)}l} } }$$应当注意的是 $G(j,k,l)$ 中 $j$ 表示频率点、 $k$ 表示分段、 $l$ 代表数据在分段内的位置,因此 $l$ 对应傅里叶变换的时间变量。严格来说,上式是离散傅里叶变换第 $m(j)$ 个点的值。其中
$$m(j)=\frac{f(j)}{r(j)}$$在 FFT 算法中, $m(j)$ 应当是整数,而此处不一定满足该要求,故LPSD算法不能利用FFT进行加速,这是该算法耗时较长的原因之一。对 $m(j)$ 的具体讨论详见文献,此处不作赘述。
在进行以上操作后,我们得到了第 $j$ 个频率点对应的 $K(j)$ 段数据 DFT 的 $K(j)$ 个单点值,对这些值进行算数平均,根据Parseval等式可得谱密度为
$$P(j) = \frac{C}{K(j)}\sum\limits_{k = 1}^{K(j)} { { {\left| {A(j,k)} \right|}^2} }$$其中 $C$ 为归一化系数,由下一节进行讨论。
功率谱的归一化
功率谱的归一化系数与窗函数相关,而窗函数可根据不同需求进行不同的选择。对于任意窗函数 $w(j,l)$ ,做如下定义
$$ \begin{gathered} {S_1}(j) = \sum_{l = 1}^{L(j)} {w(j,l)} \\ {S_2}(j) = \sum_{l = 1}^{L(j)} {{w^2}(j,l)} \end{gathered} $$单边谱的归一化系数可按下式进行计算
$$ \begin{gathered} {C_{\rm PS}}(j) = \frac{2}{{S_1^2(j)}} \\ {C_{\rm PSD}}(j) = \frac{2}{{{f_s} \cdot {S_2}(j)}} \end{gathered} $$其中, $C_{\rm PS}$ 是功率谱的归一化系数,常用于单频信号的处理。由于绝大多数信号都均匀丰富的频率成分,我们更多地采用功率谱密度,其对于的归一化系数为 $C_{\rm PSD}$ 。以电压为例,功率谱的单位是 ${\rm V}^2$,而功率谱密度的单位是 ${\rm V}^2/{\rm Hz}$。在习惯上,我们所说的功率谱指的都是功率谱密度,且取其开方值,单位为 ${\rm V}/\sqrt{ {\rm Hz} }$ 。
至此,我们依据实现的功率谱的求取,以 $f(j)$ 为横轴, $P(j)$ 为纵轴即可绘制功率谱。
不同算法的对比
依然以本文开头的数据为例,周期图法、Welch 方法以及 LPSD 算法得到的功率谱如下图所示。
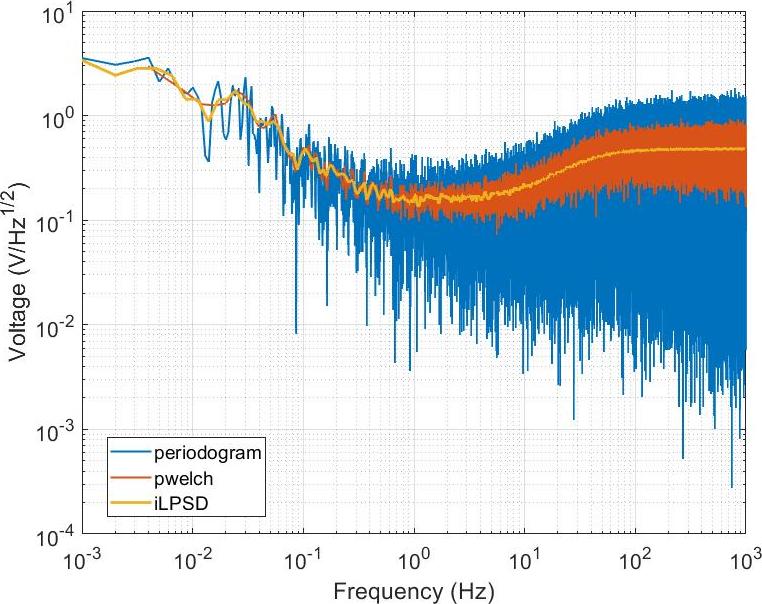
可见,LPSD 算法在低频出有更高的频率分辨率,在高频对谱密度的估计更准确,兼顾了周期图法和 Welch 方法的优点。然而 LPSD 算法牺牲了数值计算的速度,在一次利用400万个数据做谱的测试中,各算法的耗时如下。其中 iParLPSD 是利用了 MATLAB 并行工具包计算的 LPSD 算法。
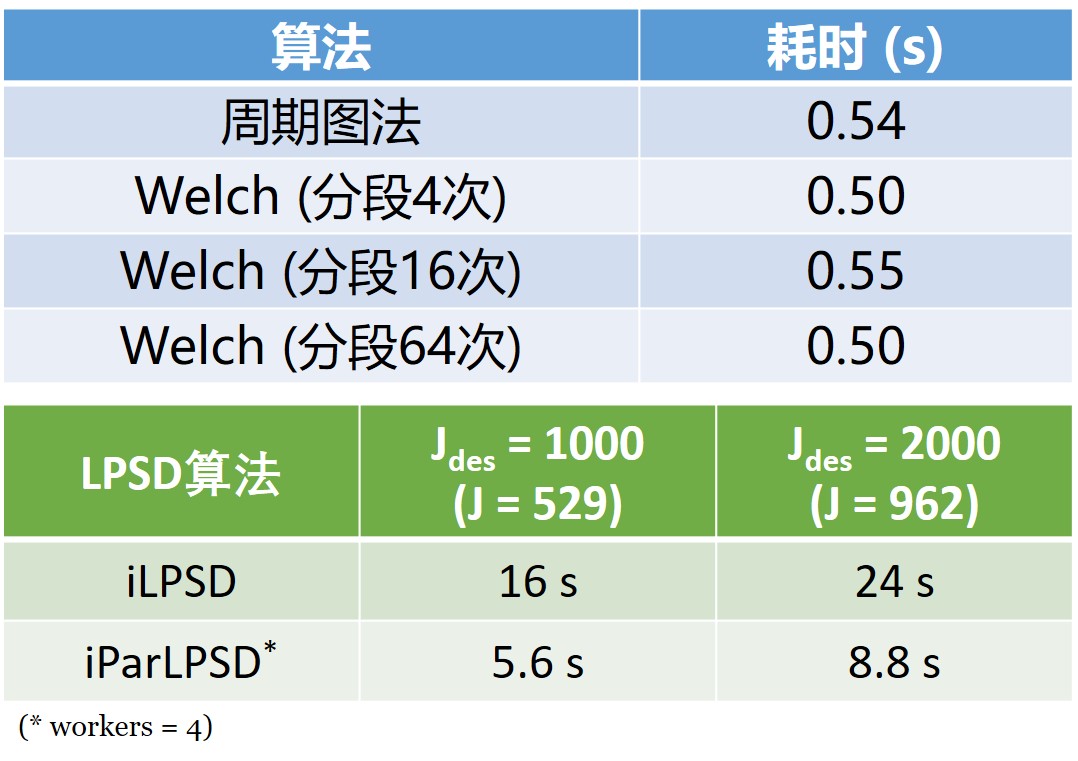
参考文献
- Michael Tröbs, Gerhard Heinzel. Improved spectrum estimation from digitized time series on a logarithmic frequency axis. Measurement. 2005.
MATLAB 源码
% Use LPSD mothod to calculate power spectral density
% Usage:
% h = iLPSD(data,fs,_)
% [pxx,f] = iLPSD(data,fs,_)
% Required paramters:
% data --- input data, processed by column
% fs --- sample frequency, unit: Hz
% Optional paramters:
% Jdes --- desired frequency points, default: 1000
% Kdes --- desired number of segments, default: 100
% xi --- overlap ratio, default: 0.5
% win --- window function handle, default: @hann
% par --- enable parallel compution, default: false
% type --- type of the sepctrum: PSD|RMS|Amp, default: PSD
% Extra paramters to control plotting are allowed (e.g. 'LineWidth')
% Output paramters
% h --- line handle of the plotted PSD
% pxx --- [PSD] one-sided PSD, unit: *^2/Hz
% [RMS| Amp] RMS or amplitude, unit: *
% f --- frequency points related to PSD points, unit: Hz
%
% Ref: Improved spectrum estimation from digitized time series on a logarithmic frequency axis
% Article DOI: 10.1016/j.measurement.2005.10.010
%
% For more information, see <a href="https://ichunyu.github.io/helps/functions/ilpsd"
% >online documentation</a>.
% XiaoCY 2019-02-23, first version (date from PPT report)
% XiaoCY 2020-04-21, support matrix data: treated as columns
% XiaoCY 2021-11-06, add inputParser to parse parameters
% XiaoCY 2022-03-28, add parameters: 'parallel', 'type'
% XiaoCY 2022-05-08, bug fix: window function in parallel mode
%% Main
function varargout = iLPSD(varargin)
% parse input paramters
p = inputParser;
p.FunctionName = 'iLPSD';
p.KeepUnmatched = true;
p.addRequired('data');
p.addRequired('fs');
p.addParameter('Jdes',1000);
p.addParameter('Kdes',100);
p.addParameter('xi',0.5);
p.addParameter('window',@hann);
p.addParameter('parallel',false);
p.addParameter('type','PSD');
p.parse(varargin{:});
% unpack necessary parameters
data = p.Results.data;
fs = p.Results.fs;
Jdes = p.Results.Jdes;
Kdes = p.Results.Kdes;
xi = p.Results.xi;
win = p.Results.window;
type = validatestring(p.Results.type,{'PSD','RMS','Amp'});
opts = p.Unmatched;
% ensure input data as column vector(s)
[N,nCol] = size(data);
if N==1 && nCol~=1
data = data';
N = nCol;
nCol = 1;
end
[f,L,m] = getFreqs(N,fs,Jdes,Kdes,xi);
J = length(f);
P = zeros(J,nCol);
if p.Results.parallel
parfor j = 1:J
Dj = floor((1-xi)*L(j));
Kj = floor((N-L(j))/Dj+1);
w = win(L(j));
l = (0:L(j)-1)';
W1 = cos(-2*pi*m(j)/L(j).*l);
W2 = sin(-2*pi*m(j)/L(j).*l);
A = zeros(1,nCol);
for k = 0:Kj-1
G = data(k*Dj+1:k*Dj+L(j),:);
G = G-mean(G); % G = detrend(G);
G = G.*w;
A = A + sum(G.*W1).^2+sum(G.*W2).^2;
end
switch type
case 'PSD'
P(j,:) = A/Kj*(2/fs/sum(w.^2));
case 'RMS'
P(j,:) = A/Kj*(2/sum(w)^2);
otherwise
P(j,:) = 2*A/Kj*(2/sum(w)^2);
end
end
else
for j = 1:J
Dj = floor((1-xi)*L(j));
Kj = floor((N-L(j))/Dj+1);
w = win(L(j));
l = (0:L(j)-1)';
W1 = cos(-2*pi*m(j)/L(j).*l);
W2 = sin(-2*pi*m(j)/L(j).*l);
A = zeros(1,nCol);
for k = 0:Kj-1
G = data(k*Dj+1:k*Dj+L(j),:);
G = G-mean(G); % G = detrend(G);
G = G.*w;
A = A + sum(G.*W1).^2+sum(G.*W2).^2;
end
switch type
case 'PSD'
P(j,:) = A/Kj*(2/fs/sum(w.^2));
case 'RMS'
P(j,:) = A/Kj*(2/sum(w)^2);
otherwise
P(j,:) = 2*A/Kj*(2/sum(w)^2);
end
end
end
switch nargout
case 0
loglog(f,sqrt(P),opts);
grid on
xlabel('Frequency [Hz]','interpreter','latex')
switch type
case 'PSD'
ylabel('PSD [$\mathrm{*/\sqrt{Hz}}$]','interpreter','latex')
case 'RMS'
ylabel('RMS [$\mathrm{*}$]','interpreter','latex')
otherwise
ylabel('Amp [$\mathrm{*}$]','interpreter','latex')
end
case 1
varargout{1} = loglog(f,sqrt(P),opts);
grid on
xlabel('Frequency [Hz]','interpreter','latex')
switch type
case 'PSD'
ylabel('PSD [$\mathrm{*/\sqrt{Hz}}$]','interpreter','latex')
case 'RMS'
ylabel('RMS [$\mathrm{*}$]','interpreter','latex')
otherwise
ylabel('Amp [$\mathrm{*}$]','interpreter','latex')
end
case 2
if strcmp(type,'PSD')
varargout{1} = P;
else
varargout{1} = sqrt(P);
end
varargout{2} = f;
otherwise
% Do Nothing
end
end
%% Subfunctions
% get logarithmic frequency points
function [f,L,m] = getFreqs(N,fs,Jdes,Kdes,xi)
fmin = fs/N;
fmax = fs/2;
r_avg = fs/N*(1+(1-xi)*(Kdes-1));
g = (N/2)^(1/(Jdes-1))-1;
f = zeros(Jdes,1)-1;
L = f;
m = f;
j = 1;
fj = fmin;
while fj < fmax
rj = fj*g;
if rj < r_avg
rj = sqrt(rj*r_avg);
end
if rj < fmin
rj = fmin;
end
Lj = floor(fs/rj);
rj = fs/Lj;
mj = fj/rj;
f(j) = fj;
L(j) = Lj;
m(j) = mj;
fj = fj+rj;
j = j+1;
end
f(f<0) = [];
L(L<0) = [];
m(m<0) = [];
end