卡尔曼滤波简介

卡尔曼滤波是一种最优滤波器，通过对系统的输入和输出进行数据融合来获得状态的最优估计。本文介绍卡尔曼滤波的基本原理并推导其核心公式。

基本思想

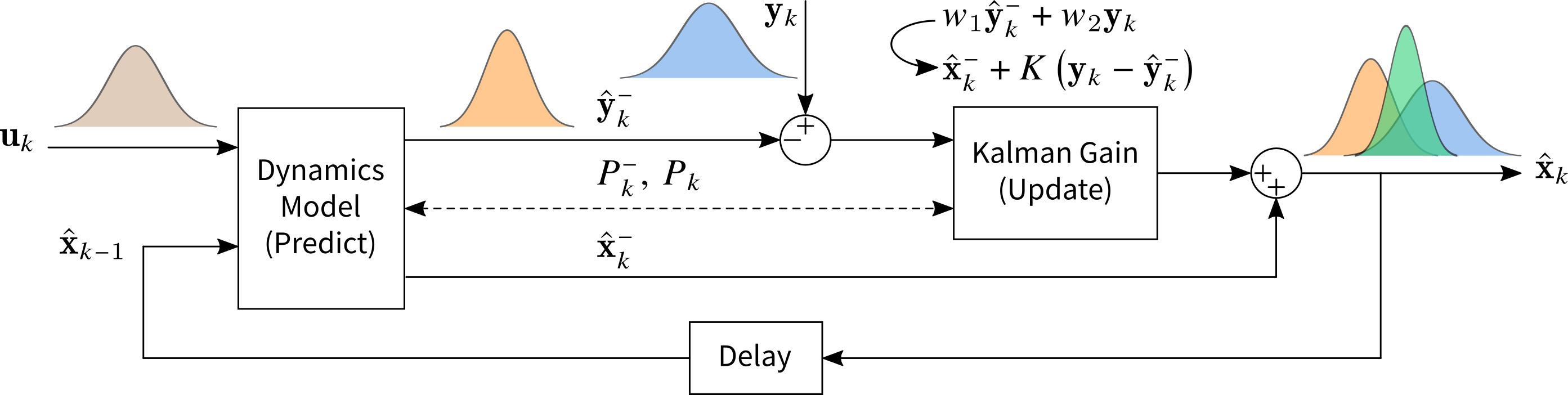
卡尔曼滤波的基本思想如下图所示：首先构建系统的动态模型，根据测得的输入对状态进行先验估计，然后依据测得的输出进行加权平均以获得最优状态估计。这种思想类似于“不等精度测量时以方差的倒数为权求加权平均”。与之不同的是，卡尔曼滤波将“各测量量加权求和”转化为“测量误差对先验估计的校正”，并且将输出折算到状态。

公式推导

设线性系统的离散状态空间方程为

$$ \left\{ \begin{aligned} \bm{x}_k &= A\bm{x}_{k-1} + B \bm{u}_k + \bm{w}_k \\ \bm{y}_k &= C \bm{x}_k + \bm{v}_k \end{aligned} \right. $$

其中 $\bm{w}$ 和 $\bm{v}$ 分别是状态噪声和测量噪声，假设他们都服从高斯分布，协方差矩阵分别为

$$\mathrm{E}(\bm{w}\bm{w}^T) = Q, \quad \mathrm{E}(\bm{v}\bm{v}^T) = R$$

由于噪声是不可知的，只能通过模型对输出估计，状态的先验估计（上标带有负号）为

$$\hat{\bm{x}}_k^- = A \hat{\bm{x}}_{k-1} + B \bm{u}_k$$

应当注意，下一步状态的先验估计由上一步状态的后验估计（上标没有负号）迭代计算，而后验估计则依据模型误差进行数据融合得到，为

$$\hat{\bm{x}}_{k} = \hat{\bm{x}}_{k}^- + K \left(y_k-C\hat{\bm{x}}_{k}^- \right)$$

定义状态估计误差：先验估计误差为 $\bm{e}_k^- = \bm{x}_k -\hat{\bm{x}}_k^-$ ，后验估计误差为 $\bm{e}_k = \bm{x}_k -\hat{\bm{x}}_k$ 。卡尔曼滤波（数据融合）的目的是使得后验估计误差最小，即

$$\mathop{\mathrm{argmin}}\limits_{K}\, \mathrm{tr}\left(P_k\right),\quad P_k = \mathrm{E}\left(\bm{e}_k\bm{e}_k^T \right)$$

下面来讨论卡尔曼增益的计算。为了迭代，将后验估计误差写成先验估计误差的迭代形式

$$ \begin{aligned} \bm{e}_k &= \bm{x}_k - \left( \hat{\bm{x}}_{k}^- + K \left( y_k-C\hat{\bm{x}}_{k}^- \right) \right) \\ &= \bm{x}_k -\hat{ \bm{x}}_k^- -KC \left(\bm{x}_k -\hat{ \bm{x}}_k^- \right) -KC\bm{v}_k \\ &= \left(I-KC \right)\bm{e}_k^- - K\bm{v}_k \end{aligned} $$

则后验估计的协方差矩阵为

$$ \begin{aligned} P_k &= \mathrm{E}\left( \left((I-KC)\bm{e}_k^- - K\bm{v}_k\right) \left((I-KC)\bm{e}_k^- - K\bm{v}_k\right)^T \right) \\ &= (I-KC)\mathrm{E}\left(\bm{e}_k^- (\bm{e}_k^-)^T\right)(I-KC)^T + K \mathrm{E}\left(\bm{v}_k\bm{v}_k^T\right)K^T \\ &\quad - (I-KC)\mathrm{E}\left(\bm{e}_k^- \bm{v}_k^T\right)K^T - K\mathrm{E}\left(\bm{v}_k(\bm{e}_k^-)^T\right)(I-KC)^T \\ &=(I-KC)P_k^-(I-KC)^T + KRK^T \end{aligned} $$

而先验估计误差的协方差矩阵为

$$ \begin{aligned} P_k^- &= \mathrm{E}\left(\left(\bm{x}_k-\hat{\bm{x}}_k^-\right)\left(\bm{x}_k-\hat{\bm{x}}_k^-\right)^T \right) \\ &= \mathrm{E}\left(\left(A\bm{e}_{k-1}+\bm{w}_{k-1}\right)\left(A\bm{e}_{k-1}+\bm{w}_{k-1}\right)^T \right) \\ &= A\mathrm{E}\left(\bm{e}_{k-1}\bm{e}_{k-1}^T \right) A^T + \mathrm{E}\left(\bm{w}_{k-1}\bm{w}_{k-1}^T \right) \\ &\quad + A\mathrm{E}\left(\bm{e}_{k-1}\bm{w}_{k-1}^T \right) +\mathrm{E}\left(\bm{w}_{k-1}\bm{e}_{k-1}^T \right)A^T \\ &= AP_{k-1}A^T + Q \end{aligned} $$

为了求解最小值问题，令 $\mathrm{tr}(P_k)$ 对 $K$ 的导数为零，其中用到矩阵论的一般结论

$$\frac{\mathrm{d\,tr}(AB) }{\mathrm{d}A} = B^T, \quad \frac{\mathrm{d\,tr}(ABA^T) }{\mathrm{d}A} = 2AB$$

因而卡尔曼增益为

$$\frac{\mathrm{d\,tr}(P_k) }{\mathrm{d}K} = -2(I-KC)P_k^-C^T + 2KR = 0 \quad \Rightarrow \quad K = P_k^-C^T\left(CP_k^-C^T+R\right)^{-1}$$

将卡尔曼增益代回 $P_k$ 可将其化简为

$$P_k = \left(I-KC\right)P_k^-$$

公式汇总

卡尔曼滤波的五个核心公式总结如下：

$$ \left\{ \begin{aligned} &\left. \begin{aligned} \hat{\bm{x}}_k^- &= A \hat{\bm{x}}_{k-1} + B \bm{u}_k \\ P_k^- &= AP_{k-1}A^T+Q \end{aligned} \quad \right\} \text{预测} \\ &\left. \begin{aligned} K &= P_k^-C^T\left(CP_k^-C^T+R\right)^{-1}\\ \hat{\bm{x}}_{k} &= \hat{\bm{x}}_{k}^- + K\left(y_k-C\hat{\bm{x}}_{k}^- \right) \\ P_k &= \left(I-KC\right)P_k^- \end{aligned} \quad \right\} \text{更新} \end{aligned} \right. $$

参考文献

1. DR_CAN 卡尔曼增益超详细推导.
2. R. Faragher. Understanding the Basis of the Kalman Filter Via a Simple and Intuitive Derivation. IEEE Signal Processing Magazine. 2012.