抗饱和积分
对于实际的系统,控制器的输出应当受到幅度限制,以避免超出执行机的量程。然而,在具有积分的控制器中如果仅对输出进行限幅,将会引起所谓的退饱和现象,使控制器的性能变差甚至导致系统不稳定。这回我们来谈谈抗饱和积分器。
退饱和现象
考察这样一种情形:积分器首先得到正值信号的输入,当积分输出达到限幅后,再经过一段时间,输入变为负值。问:积分器的输出是否会在输入信号变号的那个时刻从限福开始下降?想象一下玩 CSGO 时一直往前走直到顶到墙上,这就对应着积分限幅,这时只要按下后退键,人物立马就会离开墙面。然而遗憾的是,如果像下面这样仅仅对输出进行限幅,实际的输出可能并不会如你所愿。

不妨用仿真来看看到底是什么情况:
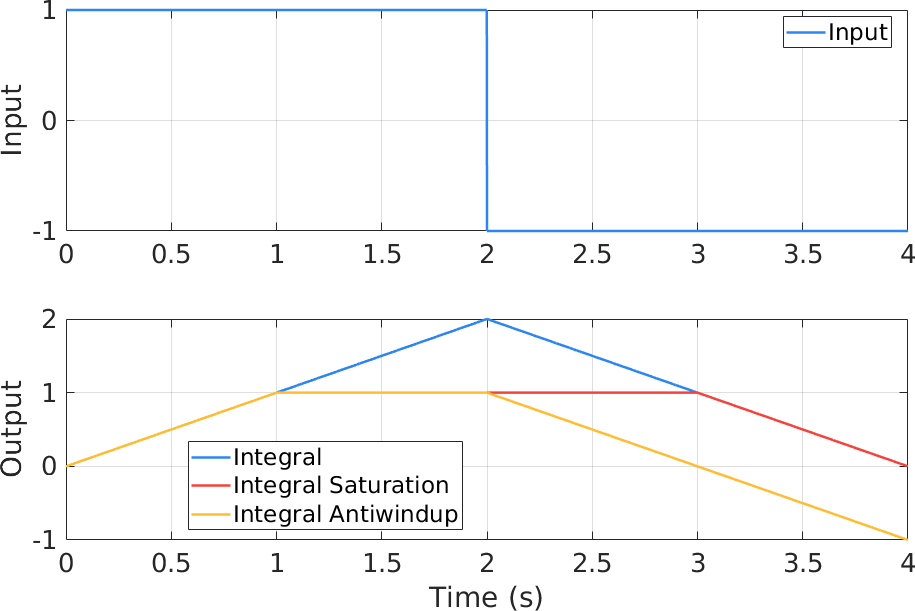
上面的子图是积分器的输入,在前 2 s 内为正, 2 s 后变为负值。积分器和限幅后的输出分别如下图的蓝色和红色曲线所示。可以看到,这种限幅并没有使输出达到饱和后停止积分,所以内部的积分仍然在持续进行,当输入变号时,积分器的输出立刻开始减小,但是仍然在限幅器的阈值之外,因此输出仍然为饱和值,直到积分减小到限幅以内。红色曲线以上的蓝色曲线下降部分就是我们所说的退饱和现象。这种现象会引起控制器输出的"延时",为了时积分的输出在输入变号时立刻开始反向积分,需要对积分进行限幅,达到图中黄色曲线的效果。
抗饱和积分器
抗饱和积分器的基本思路就是在输出达到饱和时停止积分,实现这一目的最基本的方法就是采用逻辑回路控制积分器的输入,如下图所示:
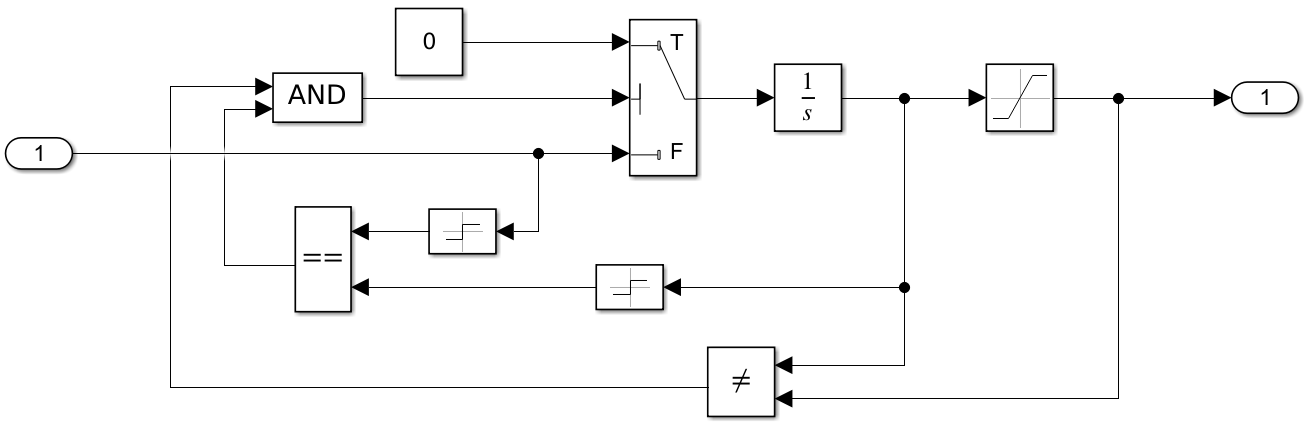
以这种方式,当积分器的输出达到饱和,且输入与输出同号,则将积分器的输入置零,避免过度积分。除了使用逻辑电路从根本上解决问题外,下面的方式展示了如何利用反馈解决这个问题:
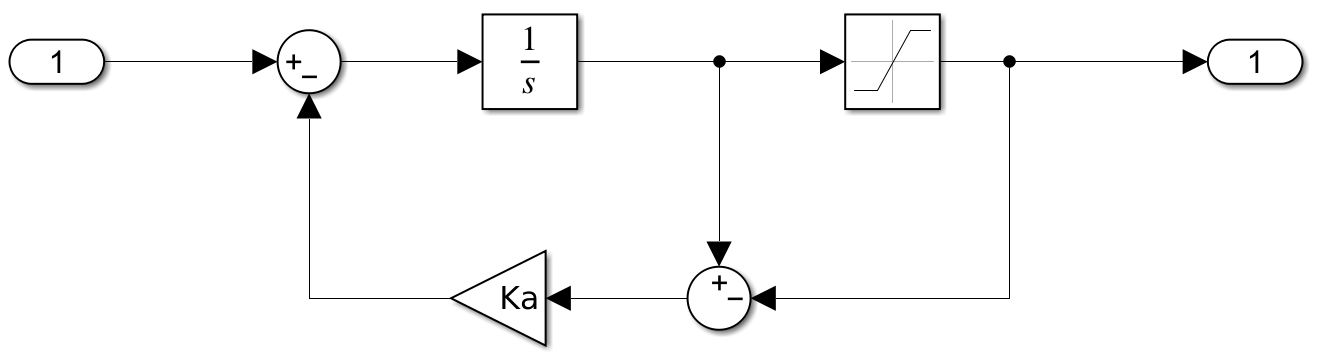
以这种方式,当积分器没有达到饱和时,反馈为零,不影响积分器的正常功能;当积分器达到饱和时,通过一个大的抗饱和增益 $K_a$ 进行误差反馈,根据稳定环路下误差趋近于零的条件,可以知道此时积分器的输入几乎为零,积分器近似停止工作。
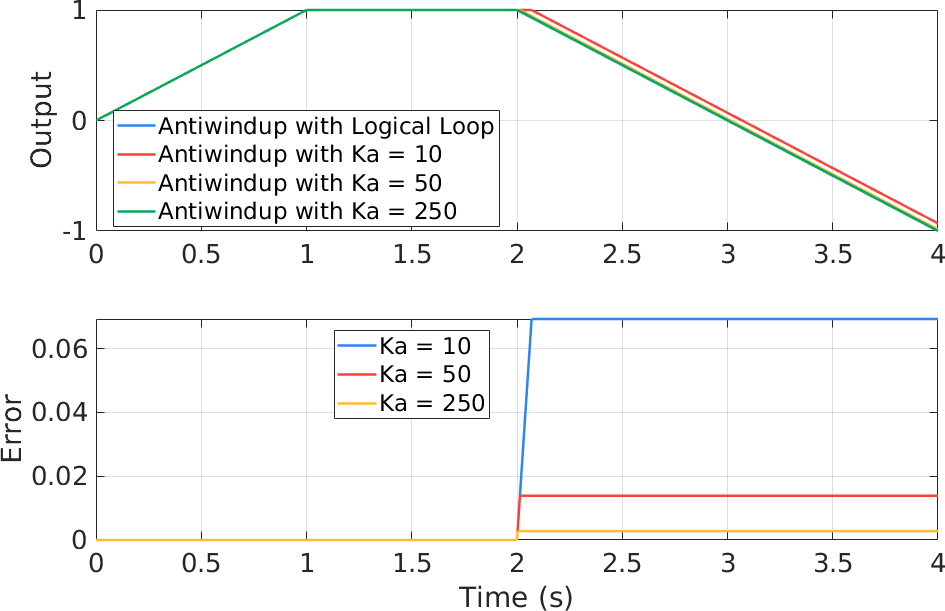
利用逻辑回路构造的抗饱和积分器是最理想的,但却难以整合在模拟电路中;利用抗饱和增益的反馈虽然具有一定的近似,但很容易在工程中实现。下图展示了这两种方式的对比,随着 $K_a$ 的增大,抗饱和反馈的方式会趋近于逻辑回路控制积分器的方式。
积分饱和对控制的影响
前面提到过,积分器的退饱和过程相当于对系统引入了不确定的延时,下面以一个例子来简单展示抗饱和积分对控制的影响。假设被控对象为一阶积分器,采用 PI 控制,如图所示:
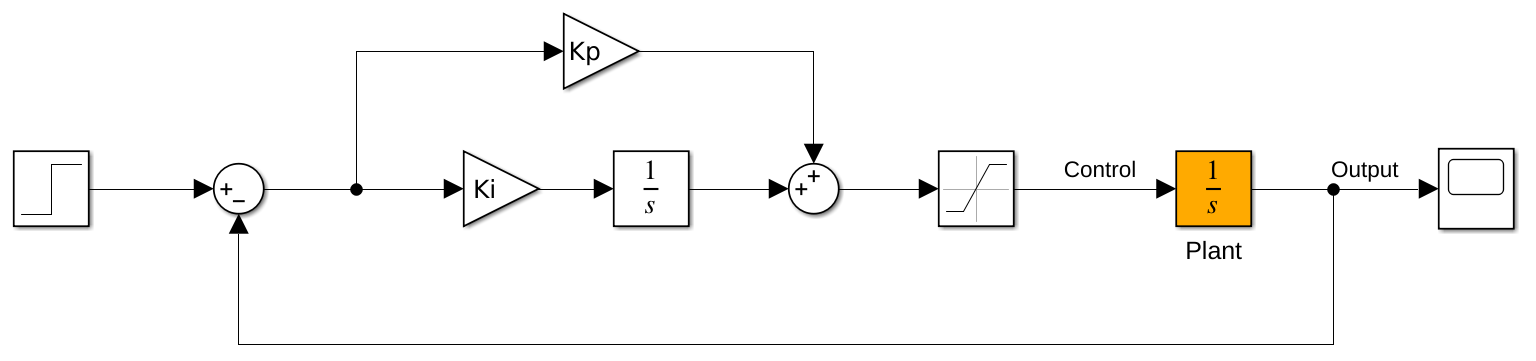
利用增益的方式对积分器进行抗饱和前后,系统的响应如下:
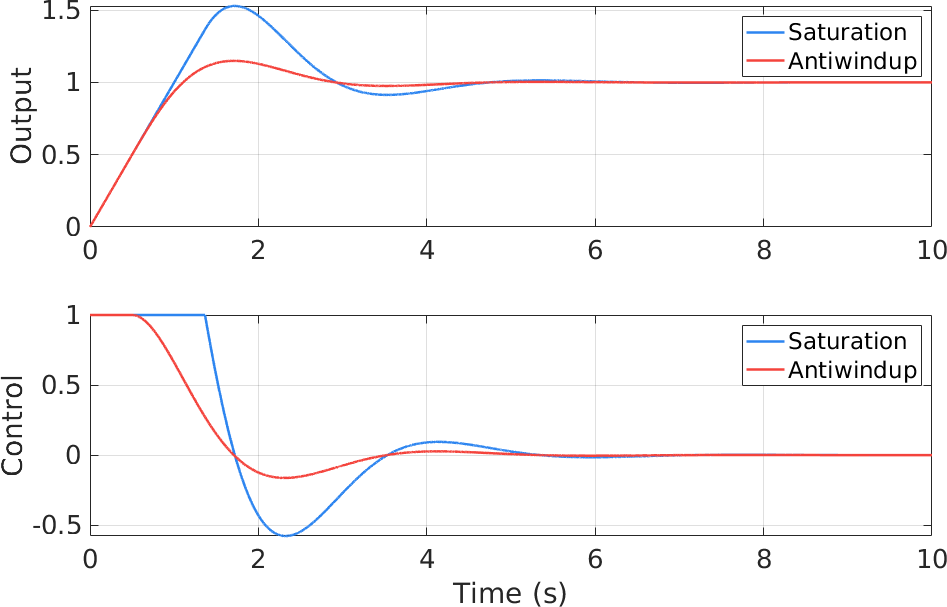
可见,如果不采用抗饱和积分器,控制命令由于退饱和而存在一定延时,导致系统的输出具有较大的超调,并因此而具有较长的收敛时间。唔,实际使用时还是得用抗饱和积分器。
参考文献
- 【中英双字】了解 PID 控制,第 2 部分:超越简单的积分 MATLAB&Simulink.
- G.F. Franklin, J. D. Powell, and A. Emami-Naeini, Feedback Control of Dynamic Systems, 7th ed. 2014.