递增子序列的最大长度

在给定的数组中进行抽取，保持元素的相对顺序不变，最长的递增序列包含多少个元素？为了求解这种递增子序列的问题，可以使用动态规划。本文简要介绍这种算法在该问题上的应用。

递增子序列

给定序列 $[x_n]$ （本文假设序列的下标从 $1$ 开始），保持元素的相对顺序进行抽取（可以全部抽取），得到其子序列 $[\breve{x}_n]$，若对于任意 $i>j$ 均有 $\breve{x}_i>\breve{x}_j$，则称 $[\breve{x}_n]$ 是 $[x_n]$ 的递增子序列。

例如，给定序列 $[6,7,1,4,2,3,5]$，其递增子序列可以是 $[6,7]$、$[1,4]$、$[2,3,5]$ 等，其中最长的递增子序列为 $[1,2,3,5]$，其长度为 $4$，是本问题求解的目标。

为了求解递增子序列的最大长度，最直接的思路是列举所有可能的递增子序列，找出这些子序列的最大长度即可。在给定序列的前提下，只要给出子序列最后一个数字即可确定以该数字结尾的递增子序列，据此可以遍历所有的递增子序列，从而得到所求的最大长度。然而穷举意味着大量的重复，是否可以基于之前遍历的结果进行递归？答案就是动态规划。

动态规划

求解的思路：找到以 $x_i$ 结尾的递增子序列并求解这些序列的最大长度 $y_i$，最后只要找到序列 $[y_n]$ 的最大值即可。

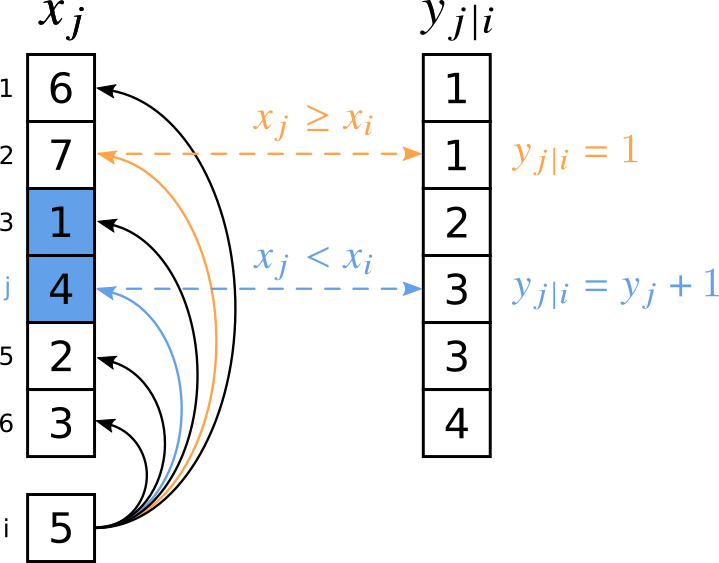
为了得到 $y_i$，试想将 $x_i$ 插入到任意 $x_{j<i}$ 后面，考察以 $x_i$ 结尾的递增子序列的最大长度 $y_{j|i}$。为了说明这一过程，如下图所示。设 $x_i=5$，当 $j=2$ 时，$x_j = 7 > x_i = 5$，此时以 $x_i$ 结尾的递增子序列为 $[5]$，长度为 $1$；当 $j=4$ 时，$x_j = 4 < x_i = 5$，意味着 $x_i$ 可以插入到 $x_j$ 后面构成递增序列。在这种情况下，递增子序列的长度是以 $x_j$ 为结尾的递增子序列最大长度加一，即 $y_j + 1$。

由此可以归纳出递归公式：

• 初始化：以第一个元素结尾的序列只包含其自己，长度为

• 将 $x_i$ 插入到 $x_j$ 之后且以 $x_i$ 为结尾的递增子序列最大长度

• 以 $x_i$ 结尾的递增子序列的最大长度：

• 给定序列的递增子序列的最大长度

代码实现

本题来自 LeetCode 的 300. 最长递增子序列，Python 代码如下：

class Solution:
    def lengthOfLIS(self, nums: List[int]) -> int:
        N = len(nums)                   # 输入序列的长度
        y = [1]*N                       # 将 x[i] 结尾的递增子序列的最大长度初始化为 1
        ymax = 1                        # 初始化序列的递增子序列最大长度
        for i in range(N):
            for j in range(i):          # 当 x[i] 插在 x[j] 后的递增子序列最大长度
                if nums[i] <= nums[j]:  
                    yji = 1
                else:
                    yji = y[j] + 1
                
                if yji > y[i]:          # y[i] 是 yji 的最大值
                    y[i] = yji
            
            if y[i] > ymax:             # ymax 是 y[i] 的最大值
                ymax = y[i]

        return ymax