产生任意谱密度的噪声
在系统仿真中通常使用噪声滤波器对白噪声进行塑形,从而验证色噪声对系统性能的影响。然而通常滤波器的阶次是整数,难以实现诸如 $1/f^\alpha , (0< \alpha <2)$ 分数阶次的粉红噪声。为此,我们可以在仿真之前利用傅立叶逆变换把噪声造出来,然后引入模型进行仿真。本文将介绍构造噪声的方法。
基本原理
制造噪声的基本思路非常简单,分为以下三步:
- 根据给定的功率谱密度计算噪声在正频率部分的频谱;
- 产生随机相位,构造噪声完整频谱;
- 利用傅立叶逆变换计算噪声时域序列。
考虑单边 ASD 与傅立叶变换的频谱之间的关系为:
$$\mathrm{ASD}(k) = \sqrt{\frac{2}{N f_s}} \left| X(k) \right|$$为了计算 $\left|X(k)\right|$,需要各频点的谱密度。在傅立叶变换中,频率点的构造应当把握以下两个原则:
- 频率从 0 Hz 开始,最大不超过采样率 $f_s$ ;
- 频率分辨率为 $f_s/N$ ,其中 $N$ 为采样点数。
由于傅立叶变换具有周期性,因而 $(f_s/2,, f_s)$ 与 $(-f_s/2,,0)$ 的频谱相同,习惯上称其为负频率部分。由于具有共轭对称性,构造频率点时只需要构造正频率部分。在 MATLAB 中可以使用以下命令:
f = (0:floor(N/2))'*fs/N;然后根据给定的 ASD 解析式即可计算正频率点频谱的模。
构造随机相位可以使用 randn 命令,然后利用复数的指数表达 $X(k) = \left|X(k)\right| \mathrm{e}^{j\phi(k)}$ 计算频谱的复数形式。为了构造完整的频谱,在利用共轭对称性时应当注意数据点的奇偶性:
- 当 $N$ 为奇数时:频率点不包含 $f_s/2$,直接将前面计算的正频率部分除了第一个 0 Hz 点之外的部分倒序共轭,并拼凑在原序列之后即可;
- 当 $N$ 为偶数时:频率点包含 $f_s/2$ ,共轭对称时要去除第一个 0 Hz 和最后一个 $f_s/2$ 的点,并拼凑在原序列之后。
构造完整频谱之后,使用 ifft 即可获得噪声的时域序列。应当注意的是,由于数值误差的存在,ifft 的输出存在很小的虚部,这是只需用 real 取其实部即可。
噪声测试
首先根据以下形式的 ASD 生成 $1/f$ 噪声:
$$\mathrm{ASD}(f) = \frac{0.05}{\sqrt{f}} + 1$$产生的噪声如下图所示,可以看出时域基本具有随机信号的特性,且 ASD 与目标基本一致,初步判定噪声满足频域形状的需求。
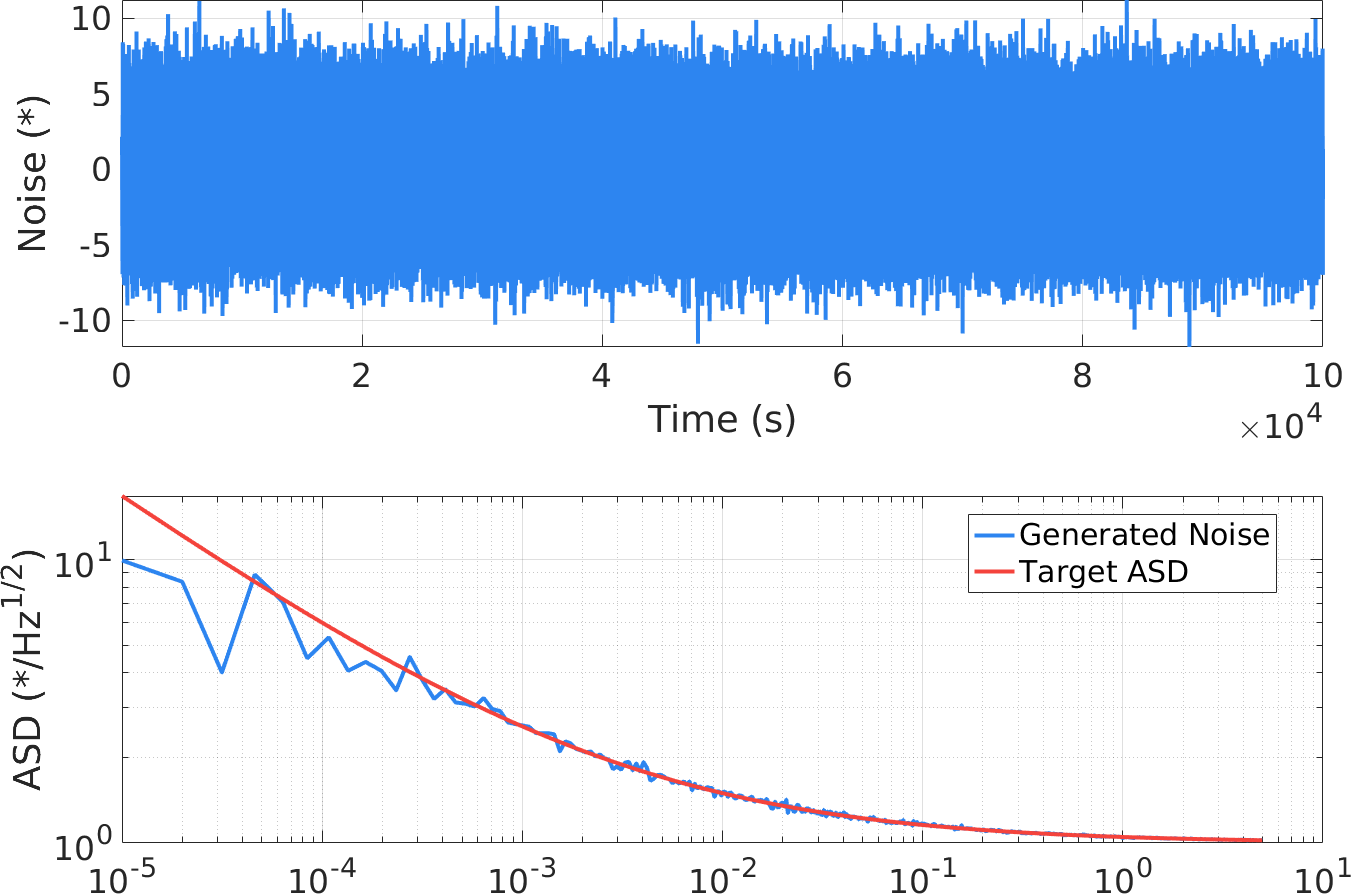
平稳随机噪声的特性应当不随时间改变,因此不同时间段的噪声应当具有相同的特性。为此,对生成的数据进行分段作谱(分段之间允许部分重叠),结果如下图所示,生成的噪声也能够满足平稳随机的要求。
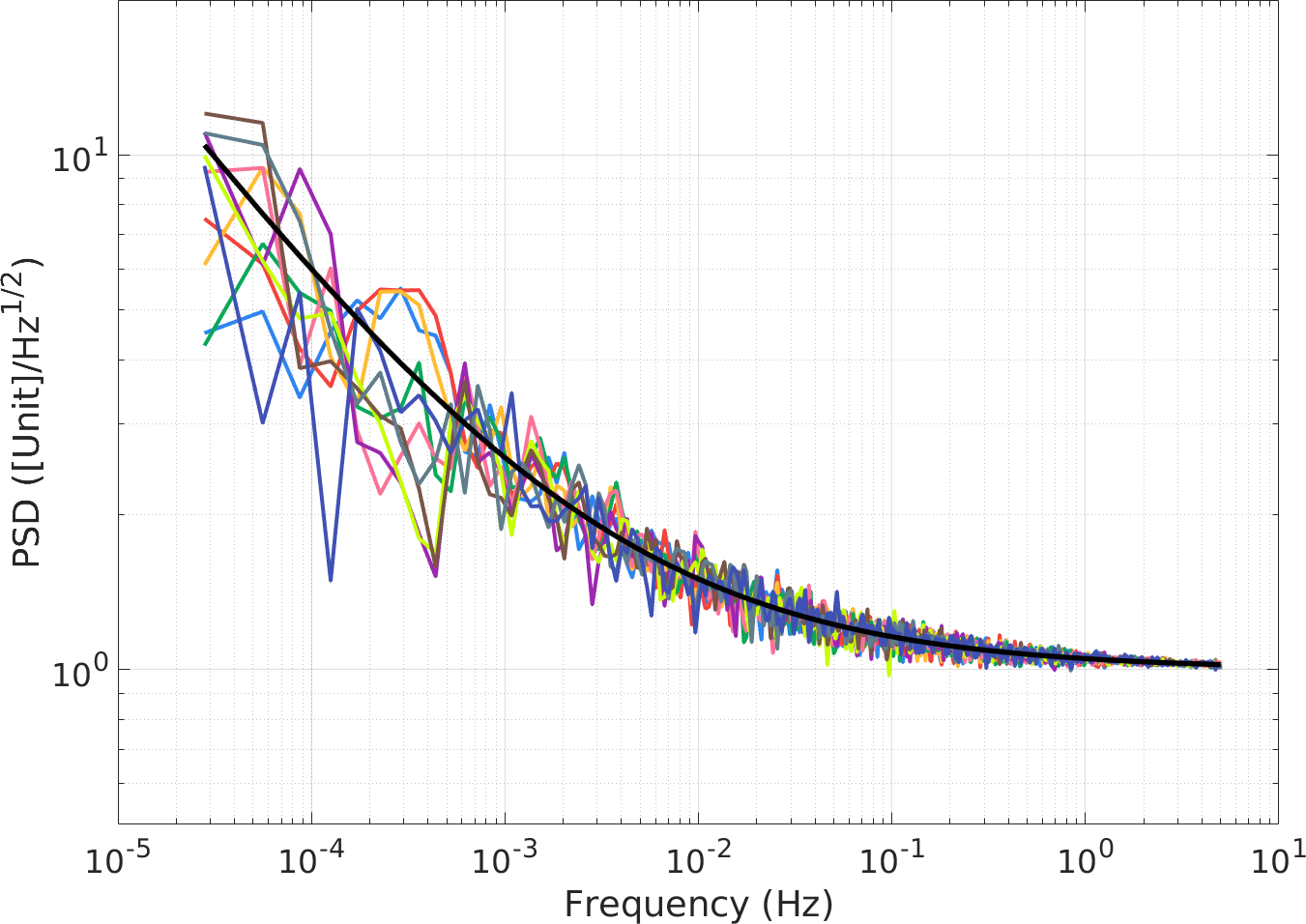
最后验证噪声的相关性:一方面自相关可以体现噪声各个时段内的相关性,理想情况下不同时段相关性为 0 ;另一方面使用相同设置生成另一组噪声,两组噪声之间应该相互独立,相关系数应当为 0 。测试结果如下图,可见满足需求。
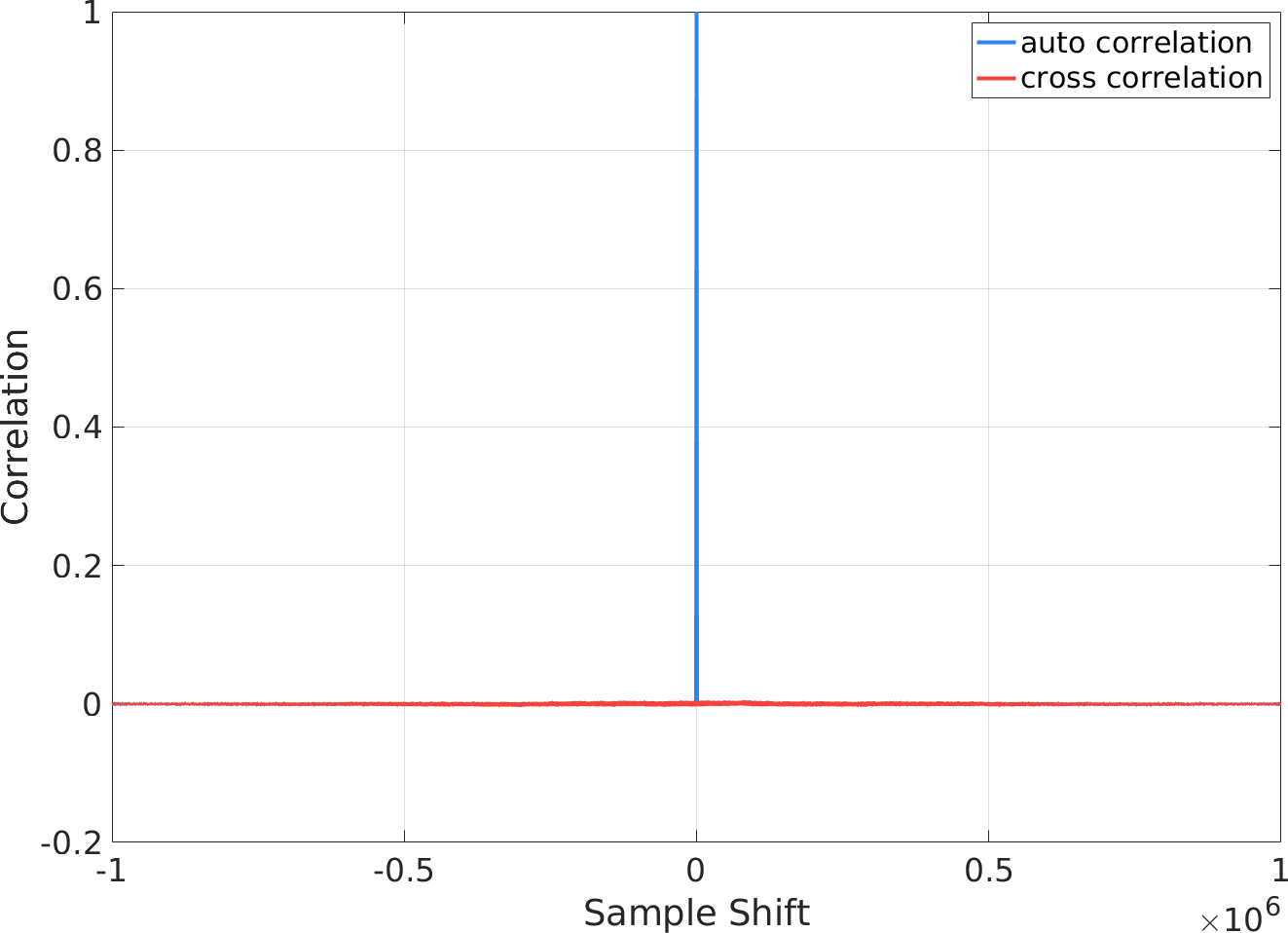
针对生成的噪声还可以进行更加严格的相关性测试,但这超出了我自己的需求,就不再过多赘述。最后展示一个频域为正弦的噪声示例(给大家看看什么叫秀,狗头保命)。
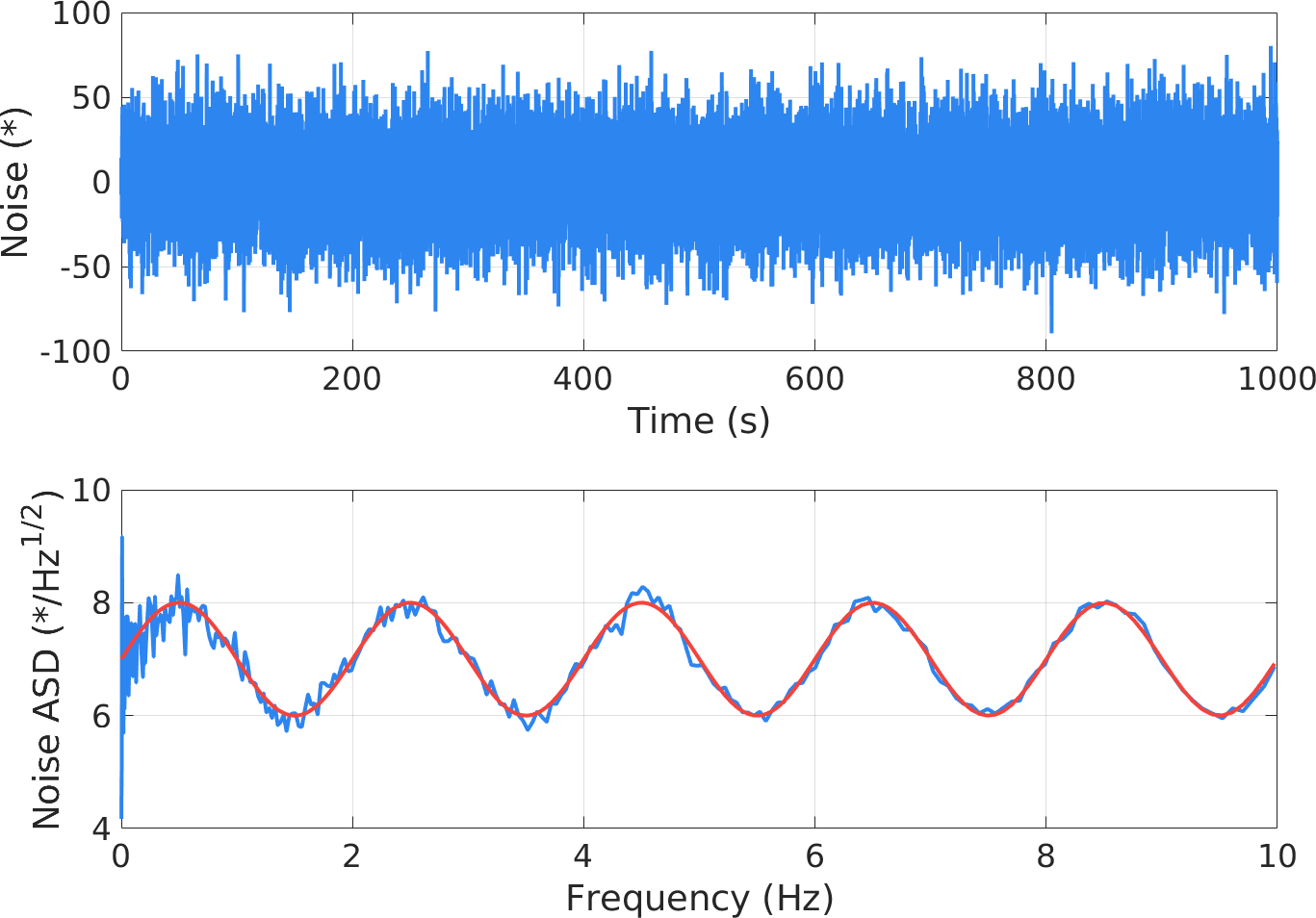
ASD = @(f) sin(pi*f) + 7;
fs = 20;
N = 1e3*fs;
x = genNoise(ASD,fs,N);
figure
subplot(211)
t = (0:N-1)'/fs;
plot(t,x)
grid on
xlabel('Time (s)')
ylabel('Noise (*)')
subplot(212)
[pxx,fx] = iLPSD(x,fs);
plot(fx,sqrt(pxx))
hold on
grid on
plot(fx,ASD(fx))
xlabel('Frequency (Hz)')
ylabel('Noise ASD (*/Hz^{1/2})')参考文献
- 宋知用. MATLAB 数字信号处理 85 个实用案例精讲: 入门到进阶. 北京航空航天大学出版社, 2016.