系统频率响应估计

2024-04-06 2024-04-07 约 1205 字预计阅读 3 分钟

系统的频率响应是控制器设计的重要依据之一，在工程上，我们常使用扫频测试来获得系统的幅频响应和相频响应，以构建经验传递函数（Empirical Transfer Functions）。本文将简要讨论系统频率响应的估计算法。

基本原理

设多输入多输出线性系统的传递函数矩阵为 $H(s)$，则输入与输出信号之间的频域关系可以表示为：

$$ \bm{y}(j\omega) = H(j\omega) \bm{u}(j\omega) $$

其中 $\bm{u}$ 和 $\bm{y}$ 分别代表系统的输入和输出向量，自变量 $j\omega$ 显式地表示该变量是傅里叶变换之后的频域表述。由于输入通常是列向量，上式无法直接对 $\bm{u}$ 求逆来计算传递函数矩阵。因此，首先考虑实值输出与输入之间的互相关函数矩阵 $R_{\bm{yu}}(t)$，其定义为：

$$ R_{\bm{yu}} (t) = \bm{y}(t) \mathop{\star} \bm{u}(t) = \int_{-\infty}^{\infty} \bm{y}(\tau) \bm{u}^\mathrm{T} (\tau-t) \,\mathrm{d}\tau $$

进一步可知 $R_{\bm{yu}}(t)$ 的傅里叶变换为：

$$ \begin{aligned} R_{\bm{yu}}(j\omega) &= \int_{-\infty}^{\infty} \left( \int_{-\infty}^{\infty} \bm{y}(\tau) \bm{u}^\mathrm{T} (\tau-t) \,\mathrm{d}\tau \right) \mathrm{e}^{-j\omega t} \,\mathrm{d}t \\ &=\int_{-\infty}^{\infty} \bm{y}(\tau) \mathrm{e}^{-j\omega\tau} \left( \int_{-\infty}^{\infty} \bm{u}^\mathrm{T} (\tau-t) \mathrm{e}^{j\omega(\tau-t)} \,\mathrm{d}\tau \right) \mathrm{e}^{-j\omega t} \,\mathrm{d}t \\ &= \bm{y}(j\omega) \bm{u}^\dag(j\omega) \end{aligned} $$

式中的角标 ${()}^\dag$ 表示共轭转置。上式给出了信号的互相关函数与其傅里叶变换之间的关系，考虑到系统的传递函数矩阵，最后一个式子可以改写为：

$$ \bm{y}(j\omega) \bm{u}^\dag(j\omega) = H(j\omega) \bm{u}(j\omega) \bm{u}^\dag(j\omega) $$

于是系统的经验传递函数可以表述为：

$$ \hat{H}(j\omega) = \bm{y}(j\omega) \bm{u}^\dag(j\omega) \left( \bm{u}(j\omega) \bm{u}^\dag(j\omega) \right)^{-1} $$

需要说明的是，这里我们用 $\hat{H}(j\omega)$ 表示估计值以区别于实际传递函数，估计的误差一方面来自数据中所包含的噪声，另一方面则来自有限时长下的频谱估计误差。本文将不对这些误差展开讨论。

数据处理

根据上面的讨论，数据处理时只需要利用快速傅里叶变换（FFT）将数据转化到频域，然后按照公式计算即可。然而，实际情况与理论有所区别：

测量噪声或输入扰动会导致 FFT 算得的频谱存在误差；
数据的采样率通常远大于关注频带的上限，实际计算只需要计算低频部分即可。

因此，在实际处理的时候需要进行一定的平滑处理，最简单的方法就是在频域直接进行加权平均。基本思路如下：

将输入、输出分别进行傅里叶变换转化为频域数据，并计算对应的频率；
根据关注频段设置参考频率 $f_r$，经验传递函数将计算参考频率处的响应；
根据相邻参考频率之间的差值设置频率分辨率 $f_\mathrm{res}(i) = f_r(i+1) - f_r(i)$。特别地，当差值计算的频率分辨率小于预设的最小分辨率时应当予以修正；
对于任意参考频率 $f_r(i)$，查找频率在 $\left( f_r(i) - f_\mathrm{res}(i),\, f_r(i) + f_\mathrm{res}(i) \right)$ 区间内 FFT 的数据点，对其加权后求解对应点的互相关函数值，并进一步按照公式得到频率响应；
整理参考频率和对应的响应，得到经验传递函数。

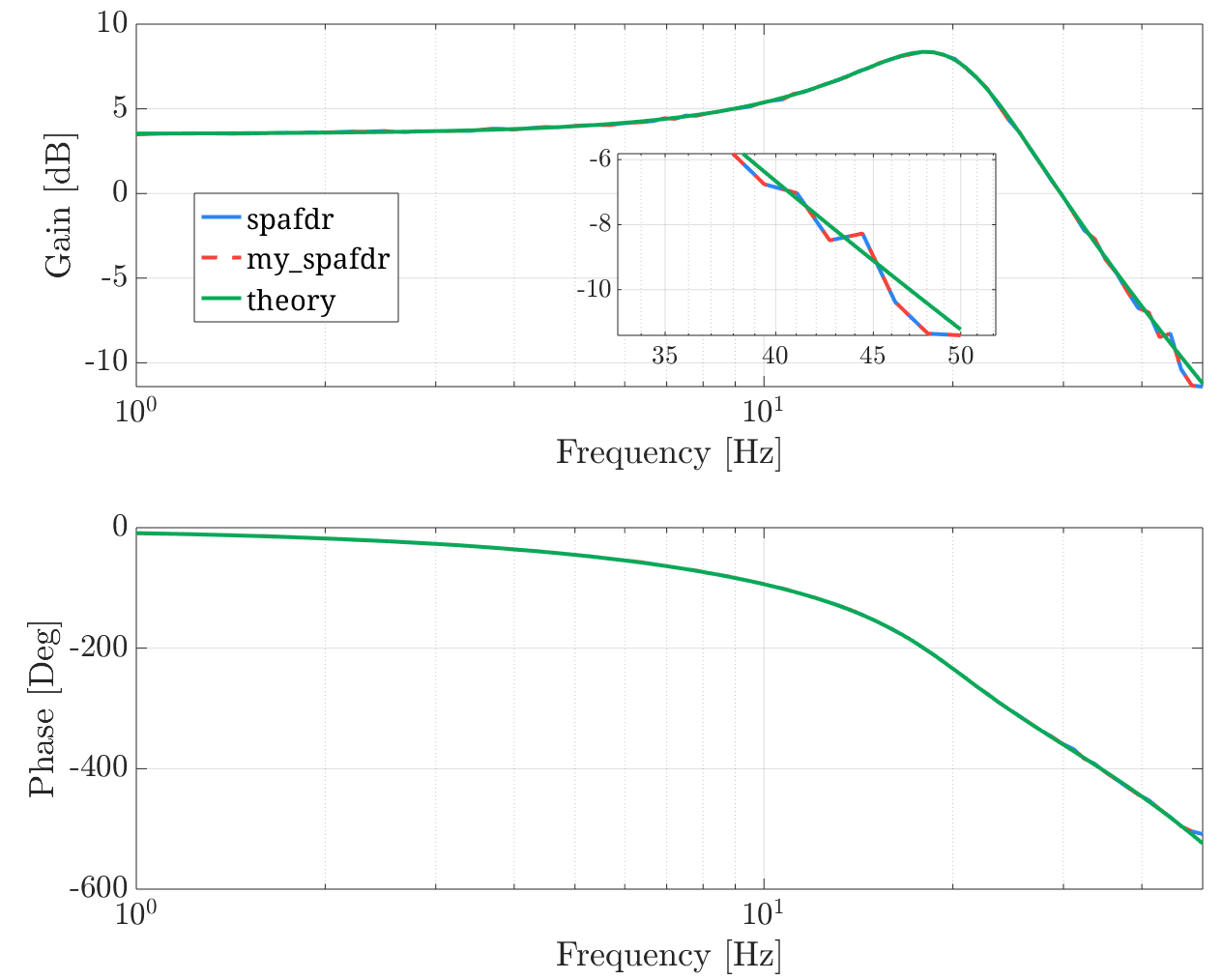
实际上，这正是 MATLAB 中 spafdr 函数的核心，根据这个思路自编的函数与 MATLAB 原生程序的对比如下：

matlab

% mdl = my_spafdr(y, u, f, fs)
% A simplifed function for MATLAB `spafdr` used for algorithm demonstration
% ASSUME: SISO system, meaning that y and u are scalar input (recorded as column vectors)
%    y --- [column vector] system output
%    u --- [column vector] system input
%   fr --- [Hz, column vector] frequency bins where to get system response
%   fs --- [Hz]sampling frequency

% XiaoCY 2024-04-06

%%
function mdl = my_spafdr(y, u, fr, fs)
    % y and u must be the same length, but I don't check here
    nfft = length(y);

    % calculate frequecy spectrum
    Y = fft(y);
    U = fft(u);
    f = (0:nfft-1)'/nfft*fs;

    % calculate frequency resolution
    fres = [diff(fr); fr(end)-fr(end-1)];
    fmin = fs/nfft;
    fres(fres < fmin) = fmin;                       % requested frequency resolution must not be less than the valid resolution

    % calculate cross-correlation and auto-correlation in frequency domain
    K = length(fr);
    [Ryu, Ruu] = deal(zeros(K,1));
    for k = 1:K
        % get index of raw spectrum data within requested resolution
        idx = abs(f - fr(k)) < fres(k);
        
        % set weighting function
        weight = cos((f(idx)-fr(k))/fres(k)*pi/2);
        % weight = weight / sum(weight);            % not necessary here, we will divide this common factor

        % calculate weight-averaged correlation
        Ryu(k) = (Y(idx).*conj(U(idx))).'*weight;
        Ruu(k) = (U(idx).*conj(U(idx))).'*weight;
    end

    % get response in frequency domain and convert to frd model
    resp = Ryu./Ruu;
    mdl = idfrd(resp, 2*pi*fr, 1/fs);
end

目录

系统频率响应估计

基本原理

数据处理