基于五点的数据处理算法
五点法是采用五个样本点对数据进行处理的一类方法,可以对数据进行平滑或微分处理。本文将讨论五点法的基本思路,并介绍 LISA 团队使用五点法处理二阶微分时的改进。
我们之前在 信号的微分 那篇文章里从控制系统的角度介绍了跟踪微分算法,那是一种满足因果性的算法,意味着当前数据的平滑(滤波)和微分不依赖于将来的数据。与之不同的是,五点法在处理当前时刻的数据时需要使用未来的数据,因此通常用于已经得到数据之后的离线处理。五点法基于当前时刻附近五个数据点的一类处理方法,本文将讨论五点法的三种设计思路,分别为泰勒级数法、参数估计法和 LISA 的二阶微分法。
泰勒级数法
泰勒展开为讨论数据在附近短时间内的变化规律提供了基本线索,记时域数据 $y(t)$ 的采样时间为 $T$,则 $t=nT$ 附近的低阶泰勒级数可以表述为:
$$ y(nT+kT) = \alpha_0 + \alpha_1 kT + \alpha_2 (kT)^2 + \alpha_3 (kT)^3 + \alpha_4 (kT)^4 + \mathscr{o}(T^5) $$式中幂级数的系数 $\alpha_k$ 与 $y(t)$ 的导数关系为:
$$ \left.\frac{\mathrm{d}^ky}{\mathrm{d}t^k}\right|_{t=nT} = \alpha_k k! $$分别取 $k=\{-2,-1,0,1,2\}$ 并舍去式中的高阶小量,利用 $y(nT+kT)$ 的数据可以构造方程组:
$$ Y_5(n,T) = \begin{bmatrix} y(nT-2T) \\ y(nT-T) \\ y(nT) \\ y(nT+T) \\ y(nT+2T) \end{bmatrix} = \begin{bmatrix} 1 & -2T & 4T^2 & -8T^3 & 16T^4 \\ 1 & -T & T^2 & -T^3 & T^4 \\ 1 & 0 & 0 & 0 & 0 \\ 1 & T & T^2 & T^3 & T^4 \\ 1 & 2T & 4T^2 & 8T^3 & 16T^4 \end{bmatrix} \begin{bmatrix} \alpha_0 \\ \alpha_1 \\ \alpha_2 \\ \alpha_3 \\ \alpha_4 \end{bmatrix} $$由此可以对 $\alpha_k$ 定解,进而根据系数与导数的关系,可以估计 $y(t)$ 在 $t =nT$ 附近的各阶导数为:
$$ \begin{aligned} \hat{y}(nT) &\approx \alpha_0 = \begin{bmatrix} 0 & 0 & 1 & 0 & 0 \end{bmatrix} Y_5(n,T) \\ \hat{y}'(nT) &\approx \alpha_1 = \frac{1}{12T} \begin{bmatrix} 1 & -8 & 0 & 8 & -1 \end{bmatrix} Y_5(n,T) \\ \hat{y}''(nT) &\approx 2 \alpha_2 = \frac{1}{12T^2} \begin{bmatrix} -1 & 16 & -30 & 16 & -1 \end{bmatrix} Y_5(n,T) \\ \hat{y}^{(3)}(nT) &\approx 6 \alpha_3 = \frac{1}{2T^3} \begin{bmatrix} -1 & 2 & 0 & -2 & 1 \end{bmatrix} Y_5(n,T) \\ \hat{y}^{(4)}(nT) &\approx 24 \alpha_4 = \frac{1}{T^4} \begin{bmatrix} 1 & -4 & 6 & -4 & 1 \end{bmatrix} Y_5(n,T) \end{aligned} $$该算法实际上是将原数据分段看作四次函数,并根据附近五个点进行定解,因而求解之后的函数在 $t = nT$ 处的数值与 $y(nT)$ 严格相等,即上面的第一个式子所示。然而,当数据存在噪声时,这种算法将因为过拟合而无法对数据进行平均,达不到平滑数据的效果。
在后面的对比中,我们将讨论的重点放在二阶导数,根据上面的第三式将相应的传递函数写为:
$$ D_{\mathrm{Taylor}}(z) = \frac{1}{12T^2} \left( -z^{-2} + 16 z^{-1} -30 + 16 z -z^2 \right) $$参数估计法
为了达到平滑的效果,我们将泰勒展开的阶数降低,利用最小二乘法进行“平均”。考虑二次展开的情况,利用 $t=nT$ 附近的五个点构造方程组:
$$ Y_5(n,T) = \begin{bmatrix} y(nT-2T) \\ y(nT-T) \\ y(nT) \\ y(nT+T) \\ y(nT+2T) \end{bmatrix} = \begin{bmatrix} 1 & -2T & 4T^2 \\ 1 & -T & T^2 \\ 1 & 0 & 0 \\ 1 & T & T^2 \\ 1 & 2T & 4T^2 \end{bmatrix} \begin{bmatrix} \alpha_0 \\ \alpha_1 \\ \alpha_2 \end{bmatrix} = \Gamma A $$最小二乘法的解为:
$$ A = \begin{bmatrix} \alpha_0 \\ \alpha_1 \\ \alpha_2 \end{bmatrix} = \left( \Gamma^\mathrm{T}\Gamma \right)^{-1} \Gamma^\mathrm{T} Y_5(n,T) $$因而 $y(t)$ 在 $t=nT$ 处的各阶导数为:
$$ \begin{aligned} \hat{y}(nT) &\approx \alpha_0 = \frac{1}{35} \begin{bmatrix} -3 & 12 & 17 & 12 & -3 \end{bmatrix} Y_5(n,T) \\ \hat{y}'(nT) &\approx \alpha_1 = \frac{1}{10T} \begin{bmatrix} -2 & -1 & 0 & 1 & 2 \end{bmatrix} Y_5(n,T) \\ \hat{y}''(nT) &\approx 2 \alpha_2 = \frac{1}{7T^2} \begin{bmatrix} 2 & -1 & -2 & -1 & 2 \end{bmatrix} Y_5(n,T) \end{aligned} $$上面的第一个式子指出,$\hat{y}(nT)$ 的估计值是对 $y(nT)$ 附近五个数据的加权平均,因此可以达到数据的平滑效果。
同样地,二阶微分的传递函数可以写做:
$$ D_{\mathrm{fit}}(z) = \frac{1}{7T^2} \left( 2 z^{-2} - z^{-1} -2 - z + 2z^2 \right) $$LISA 的二阶微分法
LISA 的二次微分算法主要从传递函数的层面考虑,根据上面的讨论,不失一般性地将二次微分的传递函数设为:
$$ D_{\mathrm{LISA}}(z) = \frac{1}{T^2} \left( a_{-2} z^{-2} + a_{-1}z^{-1} + a_0 + a_1 z + a_2 z^2 \right) $$将 $z=\mathrm{e}^{j\omega T}$ 带入上式,可以得到频率响应为:
$$ \begin{aligned} D_{\mathrm{LISA}}(j\omega) &= \frac{1}{T^2} \Bigl[ (a_2 + a_{-2}) \cos(2 \omega T) + j(a_2 - a_{-2}) \sin(2\omega T) \\ &\qquad + (a_1 + a_{-1}) \cos (\omega T) + j(a_1 - a_{-1}) \sin (\omega T) + a_0 \Bigr] \end{aligned} $$理想二次微分的频率响应为:
$$ D_\mathrm{ideal}(j\omega) = (j\omega)^2 = -\omega^2 $$将 $D_{\mathrm{LISA}}(j\omega)$ 与 $D_{\mathrm{ideal}}(j\omega)$ 进行对比,可以分别得到以下约束条件:
- 虚部为零:
- 直流响应为 $0$:
- 低频段内近似相等(低阶泰勒展开):
上面的约束仍不足以定解,对于数字系统,考虑在奈奎斯特频率处增加一个零点,即令 $D_{\mathrm{LISA}}(j \omega)$ 在 $\omega = \pi f_s = \pi/T$ 时为零,可补充方程为:
$$ 2 a_2 - 2 a_1 + a_0 = 0 $$因此可以解得 $a_0 = -1/2$,$a_1 = a_{-1} = 0$,$a_2=a_{-2} = 1/4$。因此 $y(t)$ 的二阶导数在 $t=nT$ 时刻的估计值为:
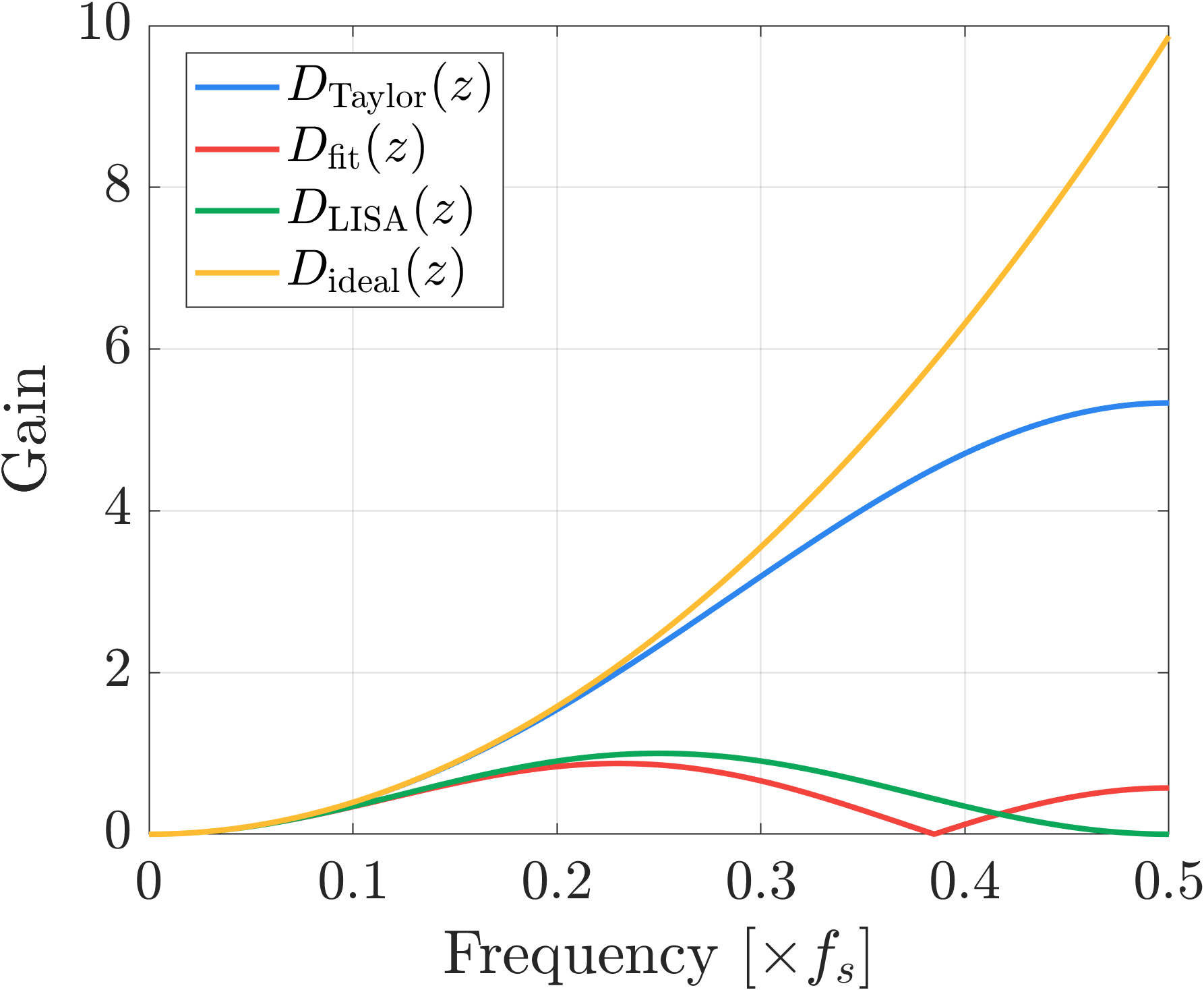
$$ \hat{y}''(nT) = \frac{1}{T^2} \Bigl( \frac{1}{4} y(nT-2T) - \frac{1}{2} y(nT) + \frac{1}{4} y(nT+2T) \Bigr) $$最后,我们将三种方法给出的二阶微分传递函数的幅频响应绘制在一起,如下图所示。其中黄色曲线为理想二次微分的幅频响应;蓝色是基于泰勒展开法的二次微分,它在很大的频率范围内与理想微分的增益一致,然而其高频增益太大,容易受到实际测量噪声的影响;红色曲线对应参数估计法,其在低频范围具有二次微分的响应,而在高频兼顾了滤波效果,其零点在奈奎斯特频率之前;绿色曲线为 LISA 的二次微分方法,相较于红色曲线,将零点挪到了奈奎斯特频率处,可以有效抑制高频噪声。
参考文献
- L. Ferraioli, M. Hueller, S. Vitale. Discrete derivative estimation in LISA Pathfinder data reduction. Classical and Quantum Gravity. 26 (2009) 094013.