信号的滤波

线性系统对不同频率信号的幅度和相位有不同的响应，据此可以实现信号在频域上的分离，这就是所谓的滤波，相应的系统称为滤波器。无论是 MATLAB 还是 Python 都具有完善的工具包对常用线性滤波器进行设计，本文简要介绍这些函数及其用法。

滤波器的参数及分类

滤波器的性能通常以其幅频响应为评估依据，主要包括以下四个参数：

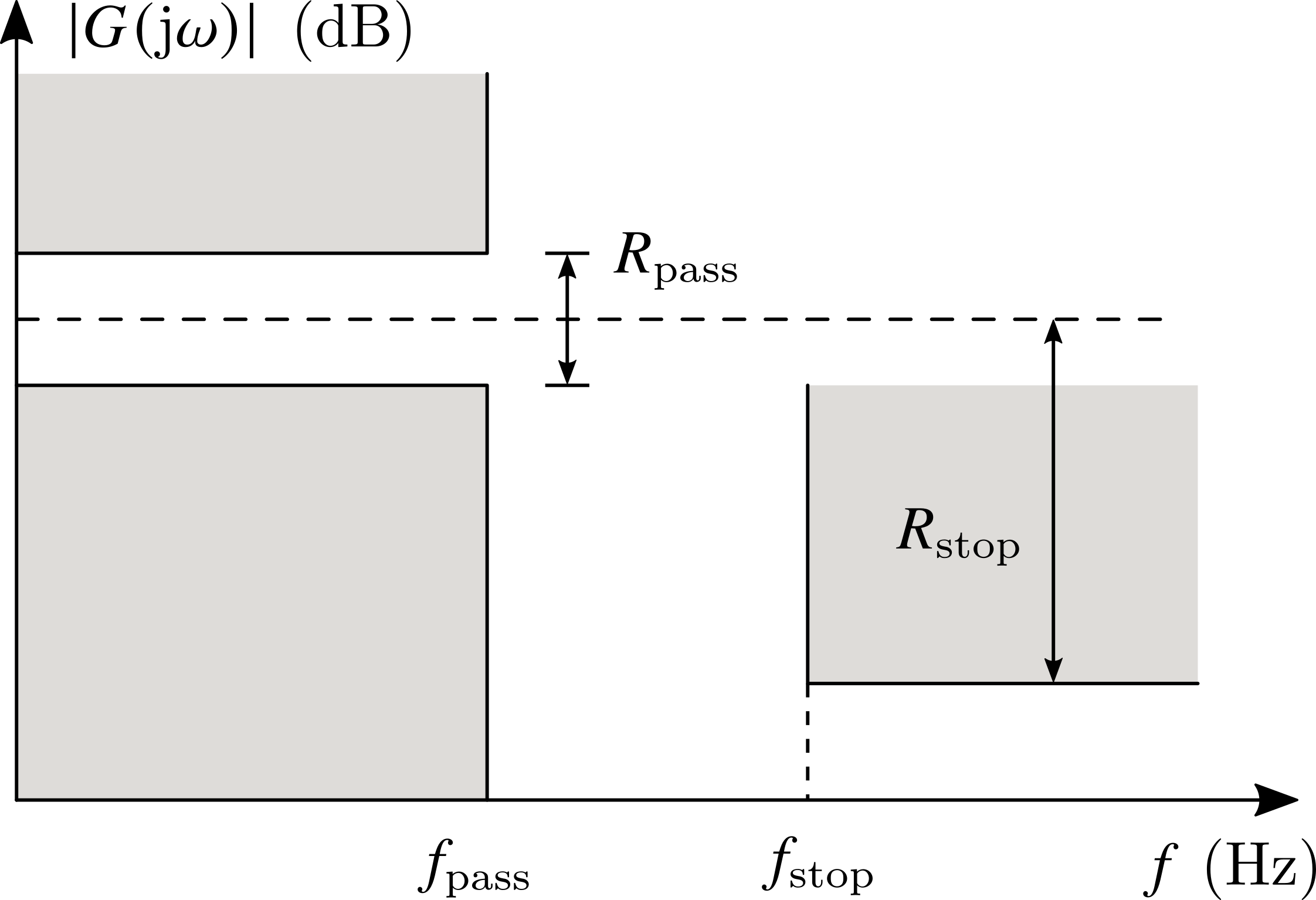
• 通带内的纹波 $R_{\rm pass}$：滤波器在通带内的增益允许波动的范围，单位为 $\rm dB$ ；
• 阻带内的衰减 $R_{\rm stop}$：阻带内的信号相比于通带信号的衰减，以 $\rm dB$ 表示；
• 通带频率 $f_{\rm pass}$：在这个频率范围内，滤波器的增益变动不超过通带纹波的约束；
• 阻带频率 $f_{\rm stop}$：在这个频率范围内，滤波器对信号的衰减达到阻带衰减倍数的需求。

以低通滤波器为例，上述四个参数可以用下图来表示

在对延时比较敏感的实时系统中，还需要讨论滤波器的群延时，其定义为相频响应的负导数，即

$$\tau_g = -\frac{\mathrm{d}\varphi(\omega)}{\omega}$$

根据滤波器实现方法的不同，可以将其分为模拟滤波器和数字滤波器，前者用于处理连续信号，主要通过模拟电路实现，以拉普拉斯变换为主要的分析工具；后者则用于处理采样后的离散信号，可以部署在各种数字器件，以 $z$ 变换为主要分析工具。

依据冲击响应还可以将滤波器分为无限脉冲响应（IIR）和有限脉冲响应（FIR），从时域上看，两者的区别在于滤波器的冲击响应是否在有限时间内收敛到 $0$ ；从频域上看，IIR 滤波器的传递函数具有至少一个极点（传递函数的分母包含 $s$ 或 $z^{-1}$），而 FIR 滤波器不具有极点，因此也称其为纯零点滤波器。

IIR 滤波器设计

常用的 IIR 滤波器有巴特沃斯滤波器、切比雪夫 I 型滤波器、切比雪夫 II 型滤波器和椭圆滤波器。为了精确指定滤波器特性，先使用函数计算滤波器的阶数和带宽，然后再对滤波器系数进行设计。在 MATLAB 中，相应的设计函数如下表所示。

滤波器	求解阶数和带宽	滤波器设计
巴特沃斯滤波器	[n,Wn] = buttord(Wp,Ws,Rp,Rs,'s')	[b,a] = butter(n,Wn,'s')
切比雪夫 I 型滤波器	[n,Wn] = cheb1ord(Wp,Ws,Rp,Rs,'s')	[b,a] = cheby1(n,Rp,Wn,'s')
切比雪夫 II 型滤波器	[n,Wn] = cheb2ord(Wp,Ws,Rp,Rs,'s')	[b,a] = cheby2(n,Rs,Wn,'s')
椭圆滤波器	[n,Wn] = ellipord(Wp,Ws,Rp,Rs,'s')	[b,a] = ellip(n,Rp,Rs,Wn,'s')

上表中， 's' 选项对应的是模拟滤波器，这时 Wp 和 Ws 的单位都是 $\rm rad/s$ ， Rp 和 Rs 的单位均为 $\rm dB$。对于数字滤波器，调用函数时应当取消 's' 选项，并且频率采用归一化的数字频率。

对于 Python 用户， scipy.signal 提供了同名的函数，使用方法基本一致，但 's' 选项应更换为关键字参数 analog=True 。

以 Wp=1 ， Ws=3 ， Rp=1 和 Rs=40 为例设计模拟滤波器，幅频响应如下图所示

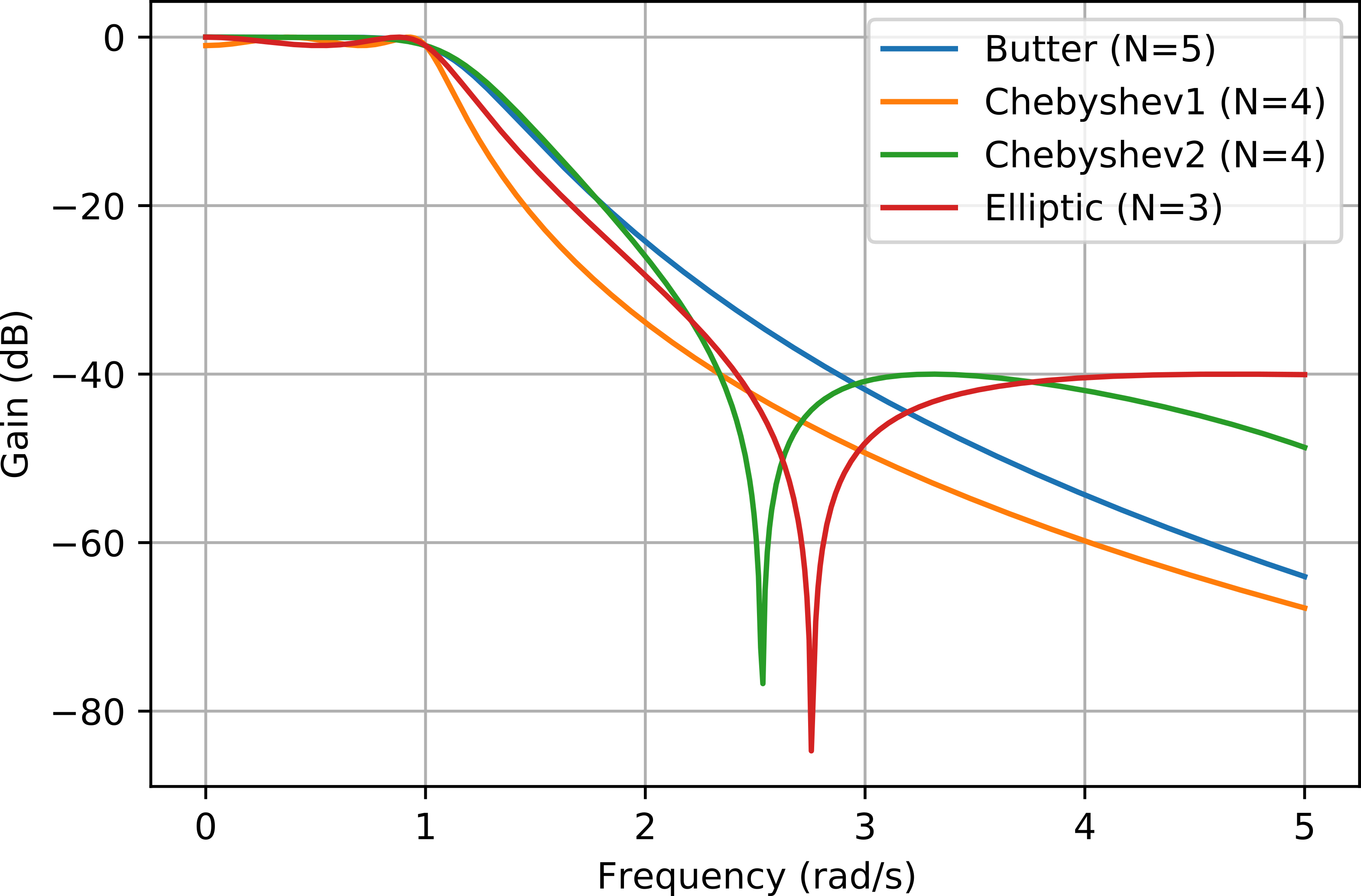
可见，在相同参数设置下：

• 巴特沃斯滤波器通带平坦，阻带无纹波，但阶数最高；
• 切比雪夫 I 型滤波器通带有纹波，阻带无纹波，阶数适中；
• 切比雪夫 II 型滤波器通带无纹波，阻带有纹波，阶数适中；
• 椭圆滤波器通带和阻带均有纹波，但阶数最少。

FIR 滤波器设计

FIR 滤波器是一种全零点数字滤波器，与 IIR 滤波器相比，不存在系统稳定性问题，且具有良好的线性相位，即滤波引入的延时是恒定的。但是为了达到相同的频率相应，FIR滤波器通常需要更高的阶数。

在 MATLAB 中，可以使用 fir1 或 fir2 进行FIR滤波器设计，前者基于窗函数设计法，设计时只需要给定滤波器阶数和带宽即可；后者基于频率采样设计法，设计时要给定阶数、频率和目标增益。

对于 Python 用户，相应的函数由 scipy.signal 包提供，分别为 firwin 和 firwin2 ，用法也是完全一致。

由于 FIR 滤波器的设计没有明确给定通带纹波、阻带衰减等特性，设计完成后通常需要验证其是否满足需求。

零相位滤波

数字滤波器的本质是差分方程，因此可以将滤波器系数转化为差分方程的系数，通过迭代实现滤波。这种动态相应通常以延时的形式表现在输出信号，如果滤波器的延时过大，可能对后续的过程产生影响。为了补偿滤波器引入的延时，有三种常用的方法：

• 互相关校准：将输出和输入的互相关来评估系统延时从而进一步补偿；
• 全通滤波器：这种滤波器在全频带内的增益都是恒定的，用于调整系统的相位以补偿前置滤波器引入的群延时；
• 零相位滤波：一种非因果的滤波技术，可以对延时进行补偿。

这里主要介绍零相位滤波，其实现方法主要有以下四步：

1. 使用通常的滤波手段（差分方程）对数据进行滤波；
2. 将滤波后的数据进行时域翻转；
3. 将翻转后的数据再次滤波；
4. 再次进行时域翻转。

从感性上看，第一次滤波是从前往后滤，因此向后引入了延时；第二次滤波是从后往前滤，向前引入的相同的"延时"。由于采用的是完全相同的滤波器，因而延时可以完全抵消。

为了使用滤波器，在 MATLAB 中可以使用 filter(b,a,x) 进行滤波，也可以使用 filtfilt(b,a,x) 进行零相位滤波。在Python中，这两个函数分别对应于 scipy.signal 中的 lfilter 和 filtfilt。下图给出同一个滤波器使用两种滤波方法对带噪声的正弦信号滤波后的结果。

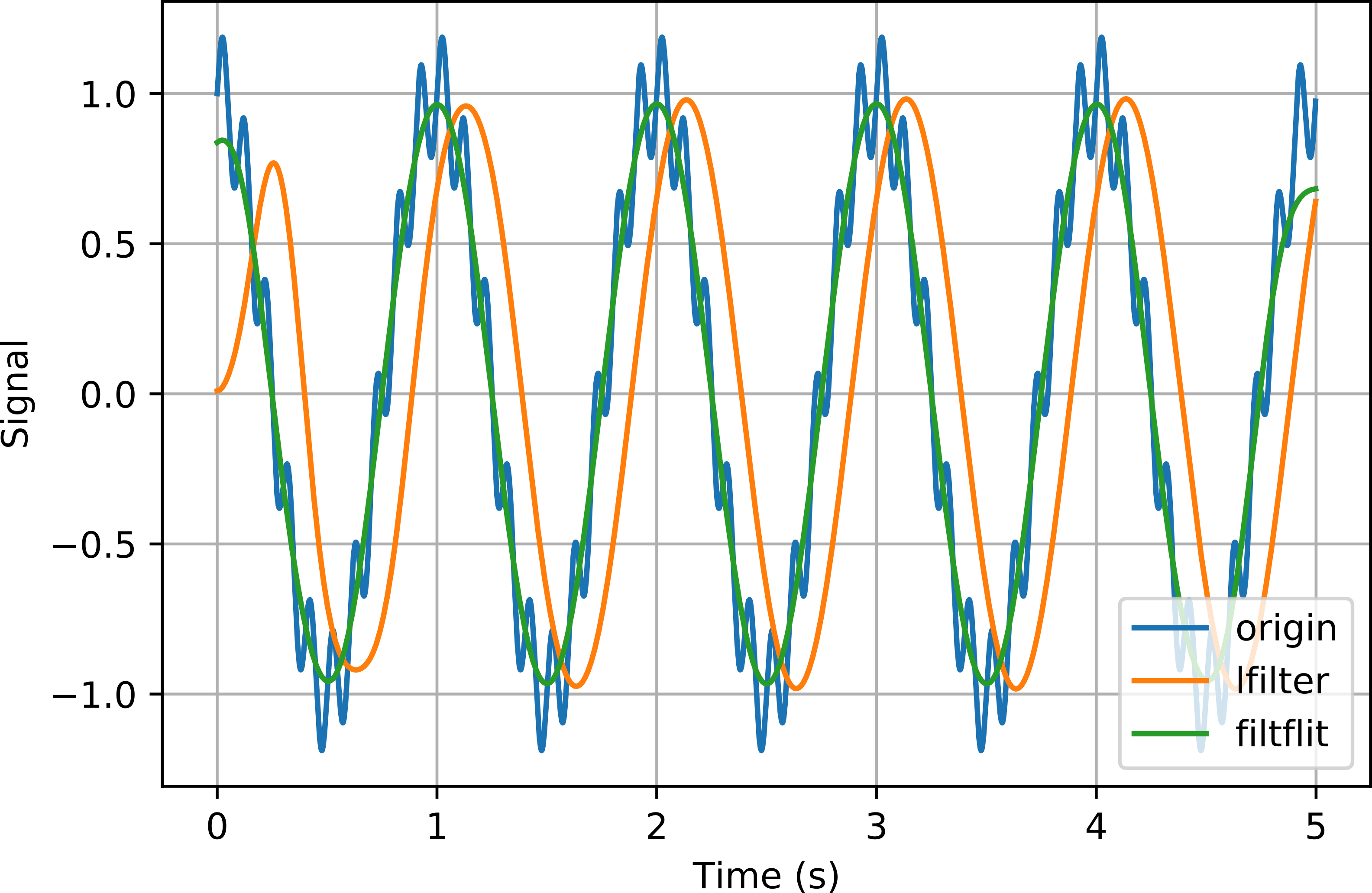
一般的滤波方法引入了可见的延时，而零相位滤波器没有引入明显延时。此外，相同滤波器下，零相位滤波器的输出结果更光滑，这是因为它对数据进行了两次滤波，其增益特性将是一次滤波的平方。需要注意的是，一般的滤波只在数据的开始阶段存在过渡过程，而零相位滤波在数据两端都有过渡过程。为了消除这些过渡过程，可以使用自适应技术提前对数据进行一定程度的预测。

零相位滤波是在数据采集完成之后才能进行的操作，不能实时处理，这也就是所谓"非因果系统"的实际含义。对于实时系统，只能通过其他的手段对延时进行补偿。