模型嵌入控制(6):带宽与极点配置
依据模型完成状态预测器和控制律设计后,控制器结构基本确定,环路性能将由参数决定。在分离原理的加持下,本文首先讨论理想控制环路和状态预测环路的带宽约束,最后给出极点配置的具体实现。
带宽的标准设计
模型嵌入控制由状态预测器、控制律和参考发生器构成,其中参考发生器独立于闭环设计,可以根据实际需求灵活设计,从环路上看来是指令的前置滤波器,因而在闭环的参数设计中不予考虑。根据 模型嵌入控制简介 中给出的系统基本架构,以单输入单输出系统为例,传递函数的形式可以表述为下图所示:
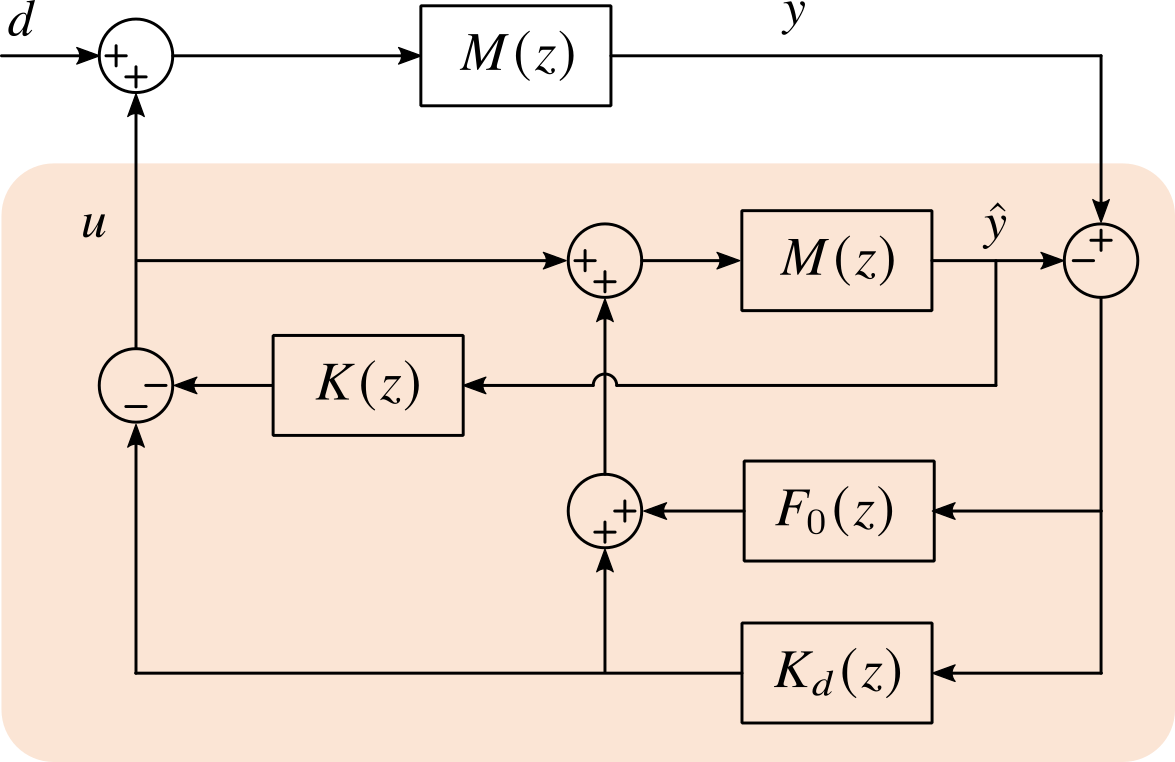
图中假设模型建模准确,可控动态的传递函数为 $M(z)$;状态预测器中可预测部分扰动的传递函数为 $K_d(z)$、随机噪声部分的传递函数记为 $F_0(z)$;$K(z)$ 将状态反馈折算到嵌入模型的输出端,可以看作是 PD 控制器。
系统框图可以分为三个环路:(1)由 $M(z)$、$F_0(z)$ 和 $K_d(z)$ 构成的状态预测环路;(2)由 $M(z)$ 和 $K(z)$ 构成的理想控制环路;(3)结合被控对象 $M(z)$ 和阴影区的模型嵌入控制构成的完整系统环路。模型嵌入控制希望完整系统环路收敛到状态预测环路。
为了便于环路传递函数的计算,将模型嵌入控制的系统结构等效为如下框图:
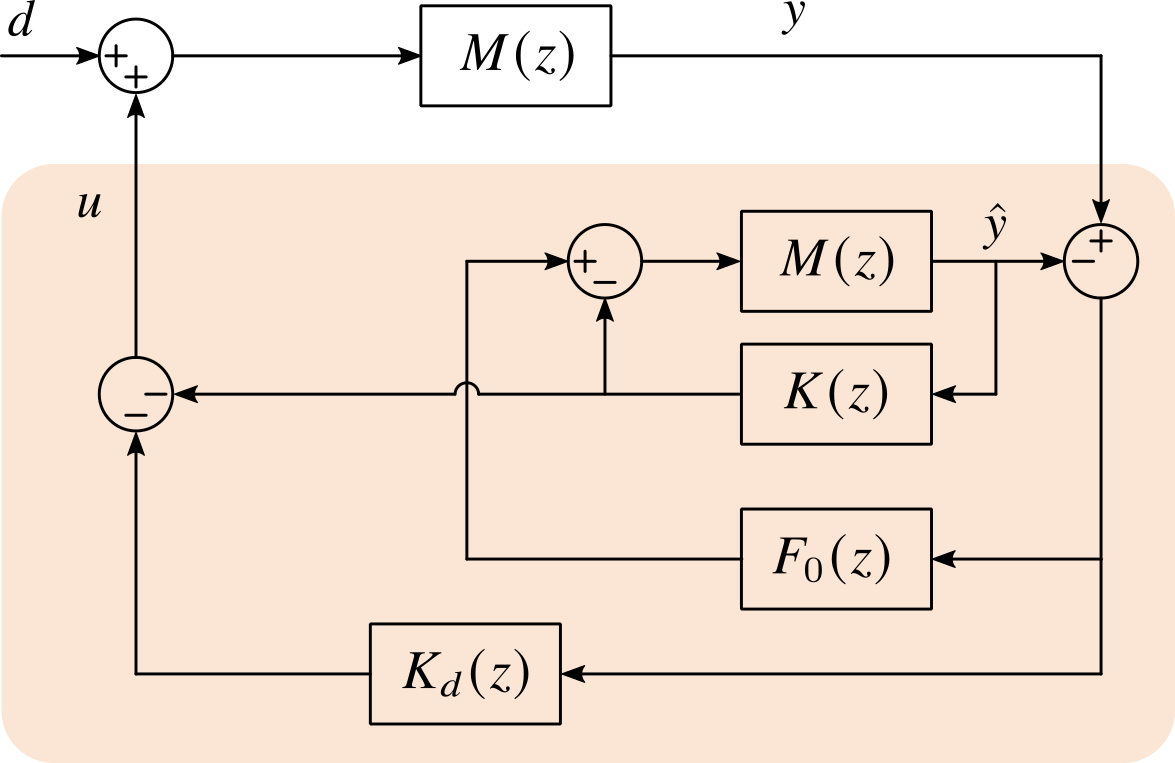
定义理想控制环路的灵敏度函数 $S_c(z)$ 和补灵敏度函数 $V_c(z)$ 分别为:
$$ S_c(z) = \frac{1}{1+M(z)K(z)} ,\quad V_c(z) = 1 - S_c(z) $$类似地,状态预测环路的灵敏度函数 $S_m(z)$ 和补灵敏度函数 $V_m(z)$ 分别为:
$$ S_m(z) = \frac{1}{1+M(z) \bigl( F_0(z) + K_d(z) \bigr)} ,\quad V_m(z) = 1-S_m(z) $$根据等效框图,可以得到模型嵌入控制的传递函数(从 $y$ 到 $u$)为:
$$ K_{\mathrm{EMC}}(z) = - \left( \frac{V_c(z) F_0(z)}{1 + F_0(z) M(z) S_c(z)} + \frac{K_d(z)}{1 + F_0(z) M(z) S_c(z)} \right) = - \frac{V_c(z) F_0(z) + K_d(z)}{1+F_0(z) M(z) S_c(z)} $$于是完整控制环路的灵敏度函数为:
$$ S(z) = \frac{1}{1+K_{\mathrm{EMC}}(z) M(z)} = S_m(z) + M(z) F_0(z) S_m(z) S_c(z) $$为了使 $S(z)$ 收敛于 $S_m(z)$,后一项应当趋近于零。其中,被控对象 $M(z)$ 通常呈现低通的形式,高频增益较小;不可预测的扰动 $F_0(z)$ 根据扰动模型具有固定的形式。因此为了使 $M(z)F_0(z)S_c(z) \ll S_m(z)$,只能通过 $S_c(z) \ll S_m(z)$ 实现,这意味着理想控制环路的带宽要远大于状态预测环路的带宽。
另一方面,我们考虑被控对象对参考指令的跟随性能,将跟踪误差做如下分解:
$$ \tilde{\bm{y}}_r = \bm{y} - \bm{y}_r = \left( \bm{y} - \hat{\bm{y}} \right) + \left( \hat{\bm{y}}_r - \bm{y}_r \right) = \tilde{\bm{y}} + C_c \bm{e}_r $$跟踪误差受到状态预测器的预测误差 $\tilde{\bm{y}}$ 和测得的跟踪误差 $\bm{e}_r$ 决定。根据 控制律设计 的讨论,$\bm{e}_r$ 可以通过理想控制环路进行抑制;考虑 状态预测器设计 所得到的设计方程,为:
$$ \left( I - S_m \partial H + V_m \partial P \right) \tilde{\bm{y}} = \bigl( S_m \partial H - V_m \partial P \bigr) \left( \bm{y}_r + C_c \bm{e}_r \right) + S_m D_y \bm{w} - V_m \bm{w}_m $$其中 $\bm{w}$ 和 $\bm{w}_m$ 均为外部随机扰动,只能通过状态预测器灵敏度函数和补灵敏度函数的设计进行一定程度的抑制;为了避免跟踪误差通过不确定性 $\partial H$ 和 $\partial P$ 影响状态预测误差,希望 $\bm{e}_r$ 充分小,这又要求理想控制环路的带宽远大于状态预测环路带宽。
极点配置具体实现
系统的稳定性由闭环极点决定,参数设计的目标是通过调整设计参数将闭环极点分配到合适的位置,从而使闭环性能满足设计需求。为了不失一般性,记 $N$ 阶闭环状态空间方程的状态矩阵为 $A$,其特征多项式为:
$$ p_\lambda(A) = \bigl\lvert \lambda I - A \bigr\rvert = \prod_{k=1}^N \left( \lambda - \lambda_k \right) $$第二个等号说明特征多项式由系统极点 $\lambda_k$ 构成。对于采样时间为 $T$ 的离散时间系统,其极点 $\lambda_k$ 与连续时间系统的极点 $s_k=-2\pi f_k$ 的关系为:
$$ \lambda_k = \mathrm{e}^{s_kT} = \mathrm{e}^{-2\pi f_k T} $$定义补极点 $\gamma_k = 1-\lambda_k$,当连续时间系统极点对应的频率满足 $2 \pi f_k T \ll 1$ 时,有:
$$ \gamma_k = 1 - \mathrm{e}^{-2\pi f_k T} \approx 2 \pi f_k T $$离散时间系统的补极点与连续时间系统的极点具有近似的线性对应关系,具有更好的物理意义。使用补极点代替极点,特征方程可以改写为:
$$ p_\lambda(A) = \bigl\lvert \left( 1-\gamma \right) I - A \bigr\rvert = \bigl\lvert \left( -\gamma \right)I - \left( A - I \right) \bigr\rvert = p_{(-\gamma)} (A-I) = \prod_{k=1}^N \left( -\gamma + \gamma_k \right) $$上式最后的等号指出 $A-I$ 的特征值为补极点的相反数,记为 $\bar{\gamma}_k = -\gamma_k$。由于最后一个等式的成立,实际在配置补极点时并不需要求解高次方程,只需要让特征多项式的系数对应相等即可。借助于 MATLAB 的符号计算,极点配置的核心代码只需要以下三行:
coeff1 = charpoly(A-eye(N)); % 计算补极点(相反数)表述下的特征方程
coeff2 = poly(-gamma); % 根据目标补极点构造特征方程
S = solve(coeff1(2:end)==coeff2(2:end); % 根据特征方程系数对应相等进行求解直接使用这种方法需要注意待调参数的数量与闭环状态数量相等,且环路设计应当取保可控性和客观性。目标补极点 $\gamma_k$ 通常可以根据等比数列设计为对数均匀的形式,即:
$$ \gamma_k = 2 \pi f_0 T 2^{-\alpha \left( k-1 \right)} $$如此做,控制参数将由 $f_0$ 和 $\alpha$ 两个参数决定,单独改变 $f_0$ 容易得到近似平移的灵敏度曲线,如下图所示:
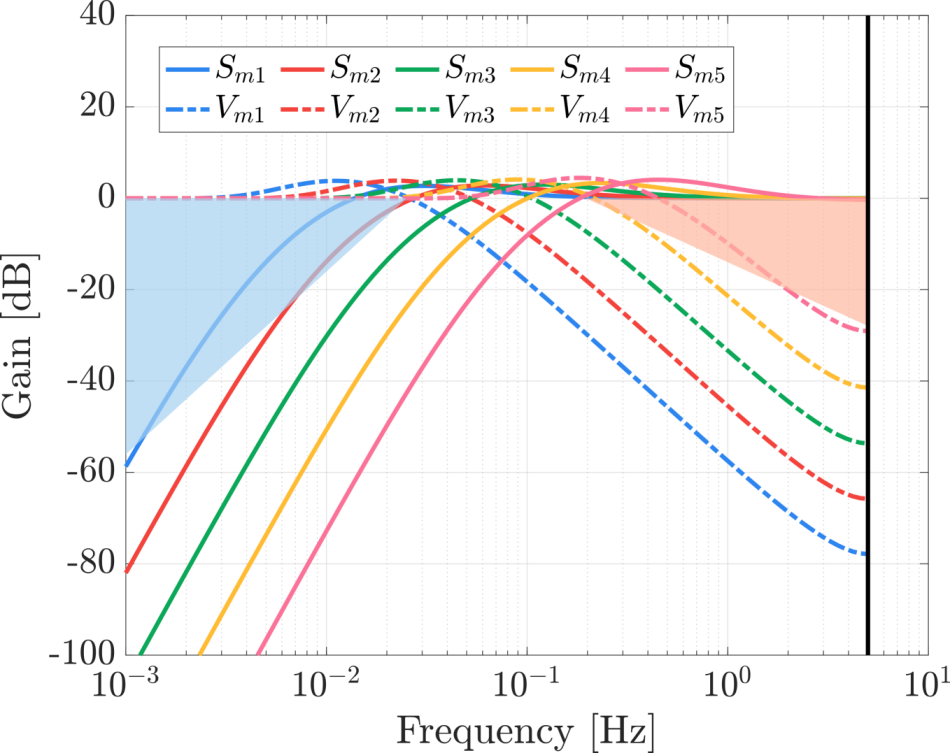
考虑到这种方法希望得到对数均匀分布的极点,在计算资源充分的情况下,我们也可以约束连续时间系统极点对应的最大、最小频率计算特征值 $\lambda$,然后再借助补极点完成计算。下面折叠的代码给出模型嵌入控制极点配置的参考程序。
% Ploe placement for EMC design
% Usage
% [Para, A] = xplace(A,p,T);
% Required paramters:
% A --- state matrix, symbilic matrix
% p --- poles or poles bound [Hz]
% T --- time unit [s]
% Optional paramters:
% Method --- place poles based on gamma or lambda, default: 'lambda'
% Tunable --- return tunable matrix 'A', default: false
% Export --- [WRANING: overwrite] export results to workspace, default: false
% Constrain --- extra equations to be used to calculate eigenvalues
%
% For more information, see <a href="https://ichunyu.github.io/helps/functions/xplace"
% >online documentation</a>.
% XiaoCY 2022-03-31, create this function
% XiaoCY 2022-04-01, add parameters
% 1. Method: place poles according to 'gamma' or 'lambda';
% 2. Tunable: return matrix A in numerical/generized form;
% 3. Overwrite: overwrite variables is workspace;
% 4. Check designed parameters;
% 5. Add built-in matrix 'A': second-order state feedbcak.
% XiaoCY 2022-04-02, change algorithm of method 'lambda'.
% XiaoCY 2022-05-31, update parameters and built-in A
% 1. add parameter 'Constrains' for extra equations;
% 2. add built-in Euler case matrix 'A'.
% XiaoCY 2022-09-13, add time unit to output struct.
% XiaoCY 2022-11-10, replace 'Overwrite' with 'Export' to make sense.
% XiaoCY 2022-11-13, [BREAKING CHANGE]
% 1. merge parameters `p1` and `p2` as a single vector `p`;
% 2. allow specified poles in `p`.
% XiaoCY 2023-04-20, enable 'PrincipalValue' in `solve`
%% main
function varargout = xplace(varargin)
p = inputParser;
p.FunctionName = 'xplace';
p.addRequired('A');
p.addRequired('p', @(x)isnumeric(x));
p.addRequired('T', @(x)isnumeric(x));
p.addParameter('Method','lambda');
p.addParameter('Tunable', false);
p.addParameter('Overwrite', false);
p.addParameter('Export',false);
p.addParameter('Constrain',[], @(s)isa(s,'sym')||isempty(s));
p.parse(varargin{:});
[A,cons] = ParseA(p.Results.A);
T = p.Results.T;
cons = [cons,p.Results.Constrain];
v = symvar(A);
N = length(A);
if length(v) ~= N + length(cons)
error('Numbers of equations and variables don''t fit.')
end
method = validatestring(p.Results.Method,{'gamma','lambda'});
Np = length(p.Results.p);
if strcmp(method, 'gamma')
if Np == 1
% all poles are the same
f0 = p.Results.p;
gamma = 2*pi*f0*T*ones(1,N);
elseif Np == 2
% p(1) as first pole, p(2) as exponent coffecient
f0 = p.Results.p(1);
alpha = p.Results.p(2);
gamma = 2*pi*f0*T * 2.^(-alpha*(0:N-1));
elseif Np == N
% p(:) are poles
f0 = p.Results.p;
gamma = 2*pi*f0*T;
end
else
if Np == 1
f0 = p.Results.p;
lambda = exp(-2*pi*f0*T)*ones(1,N);
elseif Np == 2
f1 = p.Results.p(1);
f2 = p.Results.p(2);
fk = f1*(f2/f1).^((0:N-1)/(N-1));
lambda = exp(-2*pi*fk*T);
elseif Np == N
f0 = p.Results.p;
lambda = exp(-2*pi*f0*T);
end
gamma = 1-lambda; % gamma is easier for `polychar` compution (DT system)
end
if any(gamma>1 | gamma<0)
error('Some eigenvalues are out of range.')
end
coeff1 = charpoly(A-eye(N));
coeff2 = poly(-gamma);
S = solve([coeff1(2:end)==coeff2(2:end),cons],v,'PrincipalValue',true);
Anum = eval(subs(A,S));
e = abs(eig(Anum));
if any(e>1)
warning('Cannot stabilize the system. Numerical errors may occur.')
elseif isempty(Anum)
warning('Equations are contradictory.')
end
names = fieldnames(S);
for k = 1:length(names)
eval(sprintf('Para.%s = eval(S.%s);',names{k},names{k}))
end
if p.Results.Overwrite || p.Results.Export
% This overwrites variables and could be dangerous:
for k = 1:length(names)
assignin('base',names{k},eval(sprintf('Para.%s',names{k})))
end
end
Para.T = T;
switch nargout
case 1
varargout{1} = Para;
case 2
varargout{1} = Para;
if p.Results.Tunable
for k = 1:length(names)
eval(sprintf('%s = realp(''%s'',eval(S.%s));',...
names{k},names{k},names{k}))
end
varargout{2} = eval(A);
else
varargout{2} = Anum;
end
end
end
%% subfunctions
function [A,cons] = ParseA(Ain)
if isa(Ain,'sym')
A = Ain;
cons = [];
elseif isstring(Ain) || ischar(Ain)
builtinType = {'Newton','int2',... % second-order system
'Euler','attitude',... % attitude dynamics
'K12'}; % second-order state feedback
type = validatestring(Ain, builtinType);
switch type
case {'Newton', 'int2'}
syms L0 m0 m1 m2
beta = sym('beta');
A = [
% xc1 xc2 xd1 xd2 xe
1 1 0 0 0 % xc1
-L0 1 1 0 m0 % xc2
0 0 1 1 m1 % xd1
0 0 0 1 m2 % xd2
-1 0 0 0 1-beta % xe
];
cons = [];
case {'Euler','attitude'}
syms h0 g0 h1 g1 h2 g2 L
A = [ % (see Note 2022-05-31)
% theta omega xd1 xd2 eta
1 1 0 0 0
-g0-h0 1 1 0 -h0
-g1-h1 0 1 1 -h1
-g2-h2 0 0 1 -h2
-L 0 0 0 1-L
];
cons = [g1+h1==0,g2+h2==0];
case 'K12'
syms K1 K2
A = [ 1 1; -K1, 1-K2];
cons = [];
end
else
error('Cannot parse the parameter ''A''.')
end
end参考文献
- E. Canuto, C. Novara, D. Carlucci, et al. Spacecraft Dynamics and Control: The Embedded Model Control Approach. Butterworth-Heinemann. 2018.