模型嵌入控制(4):状态预测器设计
状态预测器由可控动态、扰动动态和噪声估计器组成,能够对可控动态的状态和扰动进行一步预测。本文将讨论状态预测器的结构设计,并推导不确定性影响下的设计方程。
基于模型的状态预测器设计
状态预测器设计的核心目标是数字控制器内给出的状态收敛于被控对象的真实状态。考虑到被控对象受到的随机扰动无法完全补偿,设计的目标应当修正为状态预测误差有界。可控动态和扰动动态的状态预测误差分别定义为:
$$ \tilde{\bm{x}}_c = \bm{x}_c - \hat{\bm{x}}_c, \quad \tilde{\bm{x}}_d = \bm{x}_d - \hat{\bm{x}}_d $$根据前面对 被控对象建模 的讨论,离散时间的被控对象状态方程可以写为:
$$ \left\{\begin{aligned} & \bm{x}_c(i+1) = A_c \bm{x}_c(i) + B_c \bigl( \bm{u}(i) + \bm{h}(\bm{x}_c(i)) \bigr) + H_c \bm{x}_d(i) + G_c \bm{w}_c(i) \\ & \bm{x}_d(i+1) = A_d \bm{x}_d(i) + G_d \bm{w}_d(i) \\ & \bm{y}(i) = C_c \bm{x}_c(i) + C_d \bm{x}_d(i) \end{aligned}\right. $$基于该模型,构造形式相同并实时运行在数字控制器内的数值模型,称为嵌入模型,其状态方程为:
$$ \left\{\begin{aligned} & \hat{\bm{x}}_c(i+1) = A_c \hat{\bm{x}}_c(i) + B_c \bigl( \bm{u}(i) + \bm{h}_{\mathrm{nom}}(\hat{\bm{x}}_c(i)) \bigr) + H_c \hat{\bm{x}}_d(i) + G_c \bar{\bm{w}}_c(i) \\ & \hat{\bm{x}}_d(i+1) = A_d \hat{\bm{x}}_d(i) + G_d \bar{\bm{w}}_d(i) \\ & \hat{\bm{y}}(i) = C_c \hat{\bm{x}}_c(i) + C_d \hat{\bm{x}}_d(i) \end{aligned}\right. $$嵌入模型的状态由 $\hat{}$ 标记,表示其可以基于模型进行一步预测;而驱动噪声以 $\bar{}$ 标记以表示状态预测器只关注驱动噪声当前时刻的估计值。式中 $\bm{h}(\bm{x}_c)$ 表示被控对象状态之间由于参数不确定性或非线性引入耦合,嵌入模型中引入 $\bm{h}_{\mathrm{nom}}(\hat{\bm{x}}_c)$ 表示耦合的标称模型。
被控对象和嵌入模型的状态方程相减,可以得到状态预测误差的动态方程为:
$$ \left\{\begin{aligned} & \tilde{\bm{x}}_c(i+1) = A_c \tilde{\bm{x}}_c(i) + H_c \tilde{\bm{x}}_d(i) + G_c \bm{w}_c(i) - G_c \bar{\bm{w}}_c(i) + B_c \Delta \bm{h}(i) \\ & \tilde{\bm{x}}_d(i+1) = A_d \tilde{\bm{x}}_d(i) + G_d \bm{w}_d(i) - G_d \bar{\bm{w}}_d(i) \\ & \tilde{\bm{y}}(i) = C_c \tilde{\bm{x}}_c(i) + C_d \tilde{\bm{x}}_d(i) \end{aligned}\right. $$状态预测误差与控制指令 $\bm{u}$ 无关,会受到 $\Delta \bm{h} = \bm{h}(\bm{x}_c) - \bm{h}_{\mathrm{nom}}(\hat{\bm{x}}_c)$ 和驱动噪声 $\bm{w} = [\bm{w}_c,\,\bm{w}_d]$ 的影响。考虑将 $\Delta \bm{h}$ 线性化为:
$$ \Delta \bm{h} = \bm{h}_{\mathrm{nom}}(\bm{x}_c) + \tilde{\bm{h}}(\bm{x}_c) - \bm{h}_{\mathrm{nom}}(\hat{\bm{x}}_c) = \left. \frac{\partial \bm{h}_{\mathrm{nom}}}{\partial \bm{x}} \right\rvert_{\bm{x}=\hat{\bm{x}}_c} \tilde{\bm{x}}_c + \tilde{\bm{h}}(\bm{x}_c) $$其中,第一项的影响在状态预测误差 $\tilde{\bm{x}}_c$ 收敛时有界,可以并为随机扰动 $\bm{w}$ 的影响;第二项 $\tilde{\bm{h}}(\bm{x}_c)$ 是未知的耦合,后面将按照参数不确定性进行讨论。基于模型的环路设计中可以假设 $\Delta \bm{h} = 0$,即认为模型准确可知。
分别记可控动态和扰动动态的传递函数矩阵为 $M(z)$ 和 $D(z)$,则状态预测误差的动态可以由下图给出:
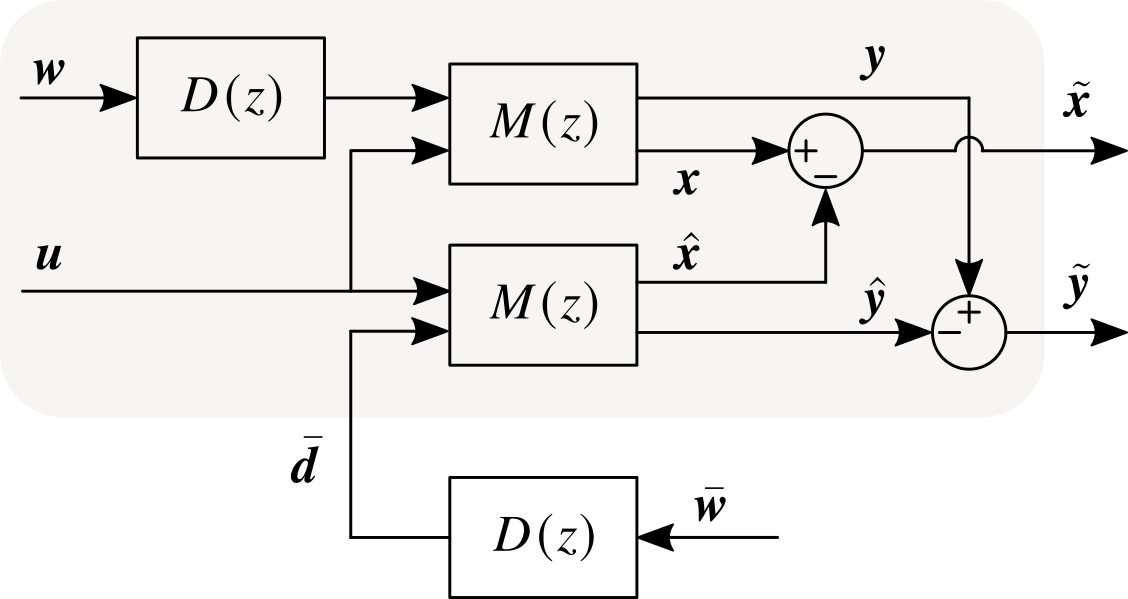
为了在随机噪声输入下使状态预测误差有界,必须构成稳定的闭环系统。由上图可知,闭环的关键是利用输出的预测误差 $\tilde{\bm{y}}$ 对驱动噪声 $\bar{\bm{w}} = [\bar{\bm{w}}_c ,\, \bar{\bm{w}}_d]$ 进行估计。不失一般性地,构造噪声估计器为:
$$ \left\{ \begin{aligned} & \bar{\bm{x}}_n(i+1) = A_n \bar{\bm{x}}_n(i) + L_n \tilde{\bm{y}}(i) \\ & \bar{\bm{w}}(i) = \begin{bmatrix} \bar{\bm{w}}_c(i) \\ \bar{\bm{w}}_d(i) \end{bmatrix} = \begin{bmatrix} N_c \\ N_d \end{bmatrix} \bar{\bm{x}}_n(i) + \begin{bmatrix} L_c \\ L_d \end{bmatrix} \tilde{\bm{y}}(i) \end{aligned} \right. $$可控动态和扰动动态分别根据被控对象和外部扰动的基本特征建模,具有特定的结构和标称参数,故状态预测器的待调参数集中在噪声估计器。从极点配置上看,噪声估计器的设计原则是引入合适数量的状态和待调参数,确保状态预测环路的总状态数量和待调参数的数量相同,从而可以对极点进行任意配置。
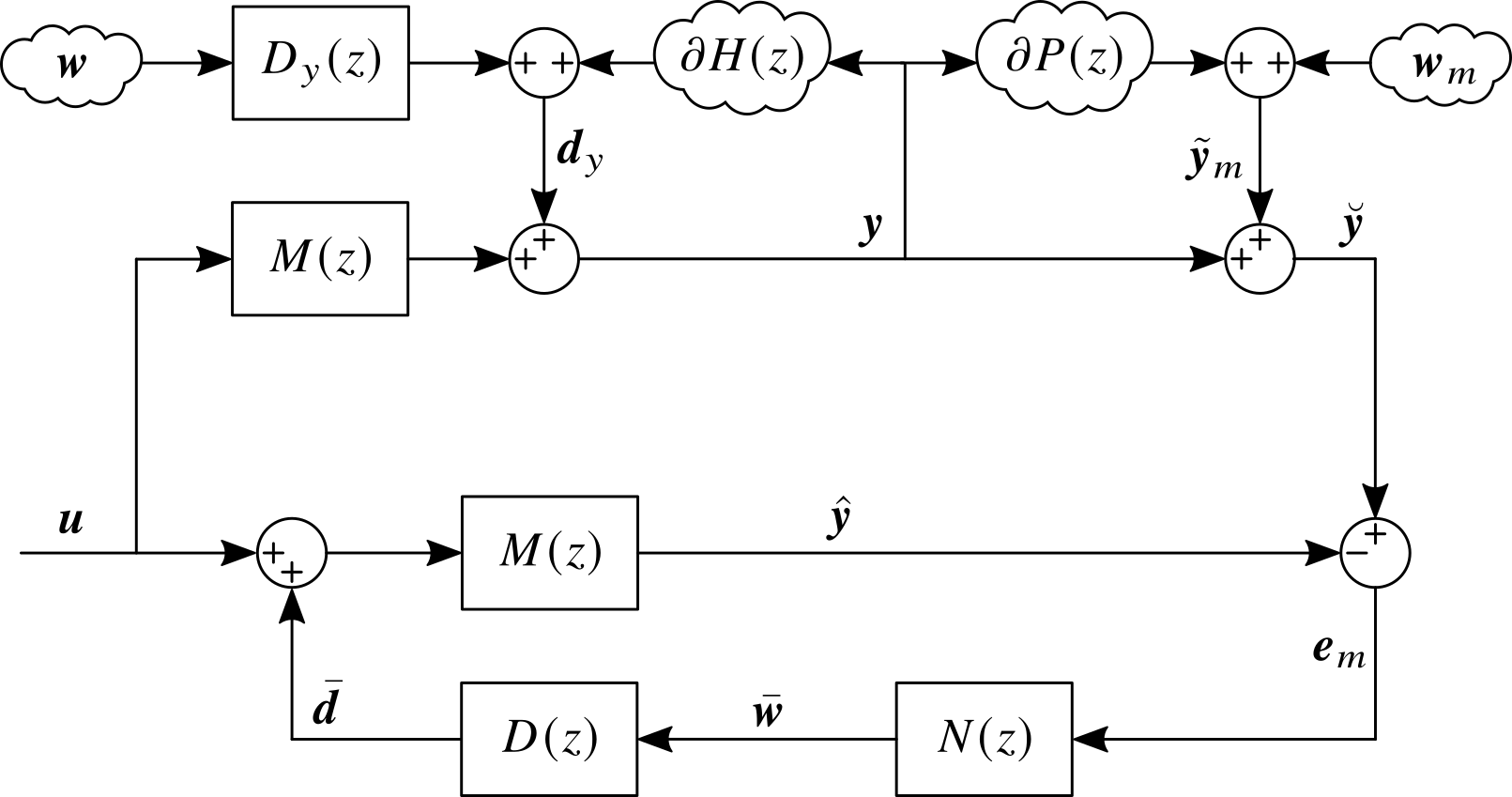
记噪声估计器的传递函数矩阵为 $N(z)$,并采用 不确定性建模 中将扰动折合到输出端的表述,被控对象和状态预测器的环路框图如下图所示。在实际应用中,输入到状态预测器的是传感器的测量值 $\breve{\bm{y}}$,因此用于噪声估计的误差由预测误差 $\tilde{\bm{y}}$ 变更为测得的模型误差 $\bm{e}_m$。
基于不确定性的设计约束
根据上图给出的环路结构,省略 $z$ 变换后的自变量,被控对象的输出和传感器测量值分别为:
$$ \bm{y} = M \bm{u} + \bm{d}_y ,\quad \breve{\bm{y}} = \bm{y} + \tilde{\bm{y}}_m $$嵌入模型的输出 $\hat{\bm{y}}$ 可以根据状态预测器的环路方程计算:
$$ \hat{\bm{y}} = M \left( \bm{u} + D N \left( \breve{\bm{y}} - \hat{\bm{y}} \right) \right) $$设被控对象传递函数矩阵 $M(z)$ 解耦为对角矩阵,状态预测器的灵敏度函数 $S_m(z)$ 和补灵敏度函数 $V_m(z)$ 可定义为:
$$ S_m = \bigl( I + DNM \bigr)^{-1},\quad V_m = I - S_m $$于是嵌入模型的输出为:
$$ \hat{\bm{y}} = S_m M \bm{u} + V_m \breve{\bm{y}} $$于是嵌入模型的输出可以改写为:
$$ \hat{\bm{y}} = S_m \left( \bm{y} - \bm{d}_y \right) + V_m \left( \bm{y} + \tilde{\bm{y}}_m \right) = \bm{y} - S_m \bm{d}_y + V_m \tilde{\bm{y}}_m $$移项后可得输出的预测误差为:
$$ \tilde{\bm{y}} = \bm{y} - \hat{\bm{y}} = S_m \bm{d}_y - V_m \tilde{\bm{y}}_m $$根据 不确定性建模 对扰动的简化和上图的示意,代入 $\bm{d}_y$ 和 $\tilde{\bm{y}}_m$ 的具体形式:
$$ \bm{d}_y = D_y \bm{w} + \partial H \bm{y}, \quad \tilde{\bm{y}}_m = \partial P \bm{y} + \bm{w}_m $$整理得:
$$ \tilde{\bm{y}} = \left( S_m \partial H - V_m \partial P \right) \bm{y} + S_m D_y \bm{w} - V_m \bm{w}_m $$该式说明:被控对象受到的外扰 $D_y\bm{w}$ 可以被状态预测器环路的灵敏度函数 $S_m(z)$ 抑制,但传感器的测量噪声 $\bm{w}_m$ 会以补灵敏度函数 $V_m(z)$ 的形式影响预测误差。参数不确定性分别以 $S_m(z) \partial H(z)$ 和 $V_m(z) \partial P(z)$ 的形式通过输出 $\bm{y}$ 耦合到预测误差。
在测量噪声的影响下,被控对象输出的真值 $\bm{y}$ 无法准确得知,利用参考信号和测得的跟踪误差进行改写,即:
$$ \bm{y} = \hat{\bm{y}} + \tilde{\bm{y}} = \hat{\bm{y}} - \bm{y}_r + \bm{y}_r + \tilde{\bm{y}} = C_c \bm{e}_r + \bm{y}_r + \tilde{\bm{y}} $$式中 $\bm{e}_r$ 为测得的跟踪误差,将在 控制律设计 中展开讨论。代入上式,可以得到状态预测器设计方程为:
$$ \left( I - S_m \partial H + V_m \partial P \right) \tilde{\bm{y}} = \bigl( S_m \partial H - V_m \partial P \bigr) \left( \bm{y}_r + C_c \bm{e}_r \right) + S_m D_y \bm{w} - V_m \bm{w}_m $$预测误差 $\tilde{\bm{y}}$ 的敛散性由 $\left( I- S_m \partial H + V_m \partial P \right)^{-1}$ 的极点决定。由于系统的不确定性使其极点无法准确评估,系统的鲁棒稳定性由下式给出:
$$ \left\lVert -S_m \partial H + V_m \partial P \right\rVert_\infty \le \left\lVert S_m \partial H \right\rVert_\infty + \left\lVert V_m \partial P \right\rVert_\infty \le \eta_m < 1 $$其中第一个不等式的防缩使设计更加保守,$\eta_m^{-1}$ 为状态预测器在不确定性下的增益裕度。
从设计方程可知,预测误差 $\tilde{\bm{y}}$ 会受到测得的跟踪误差 $\bm{e}_r$ 的影响,意味着不确定性会导致状态预测器与控制律之间存在弱耦合。一方面,$\partial H C_c \bm{e}_r$ 和 $\partial P C_c \bm{e}_r$ 可以分别看作 $D_y \bm{w}$ 和 $\bm{w}_m$ 的一部分,作为额外的扰动和测量噪声并通过状态预测器的环路设计进行抑制;另一方面,$\bm{e}_r$ 可以被控制律约束在充分小的范围,这就要求理想控制环路的带宽大于状态预测环路带宽,,称之为模型嵌入控制的标准设计(Standard Design)。
示例:二阶系统的状态预测器
从上面的推导可以看到,在假设模型准确时,被控对象、嵌入模型和状态预测误差具有相同的状态空间方程,实际设计时通常可以不必再推导状态预测误差的方程,直接基于被控对象模型进行设计。
继续 被控对象建模 示例中二阶系统的设计,其状态预测误差的方程为:
$$ \left\{\begin{aligned} & \tilde{\bm{x}}_c(i+1) = \begin{bmatrix} 1 & 1 \\ -\omega_0^2 T^2 & 1 \end{bmatrix} \tilde{\bm{x}}_c(i) + \begin{bmatrix} 0 \\ 1 \end{bmatrix} u + \begin{bmatrix} 0 \\ 1 \end{bmatrix} \bigl( w_c(i) - \bar{w}_c(i) \bigr) \\ & \tilde{\bm{x}}_d(i+1) = \begin{bmatrix} 1 & 1 \\ 0 & 1 \end{bmatrix} \tilde{\bm{x}}_d(i) + \begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix} \bigl( \bm{w}_d(i) - \bar{\bm{w}}_d(i) \bigr) \\ & \tilde{y}(i) = \begin{bmatrix} 1 & 0 \end{bmatrix} \tilde{\bm{x}}_c(i) \end{aligned}\right. $$为了从模型误差 $\tilde{y}$ 中估计驱动噪声 $\bar{\bm{w}} = [\bar{w}_c,\,\bar{\bm{w}}_d]$,假设噪声估计器为纯增益,即:
$$ \begin{bmatrix} w_c(i) \\ w_{d1}(i) \\ w_{d2}(i) \end{bmatrix} = \begin{bmatrix} l_1 \\ l_2 \\ l_3 \end{bmatrix} \tilde{y}(i) $$此时状态预测器将有三个可调参数 $\{l_1,\,l_2,\,l_3\}$,不能与四个状态变量匹配,因而无法实现极点的任意配置。为此,需要在状态预测器引入扩展状态 $\bar{x}_n$ 并引入额外的设计参数使可调参数与状态数目匹配。考虑如下状态预测器:
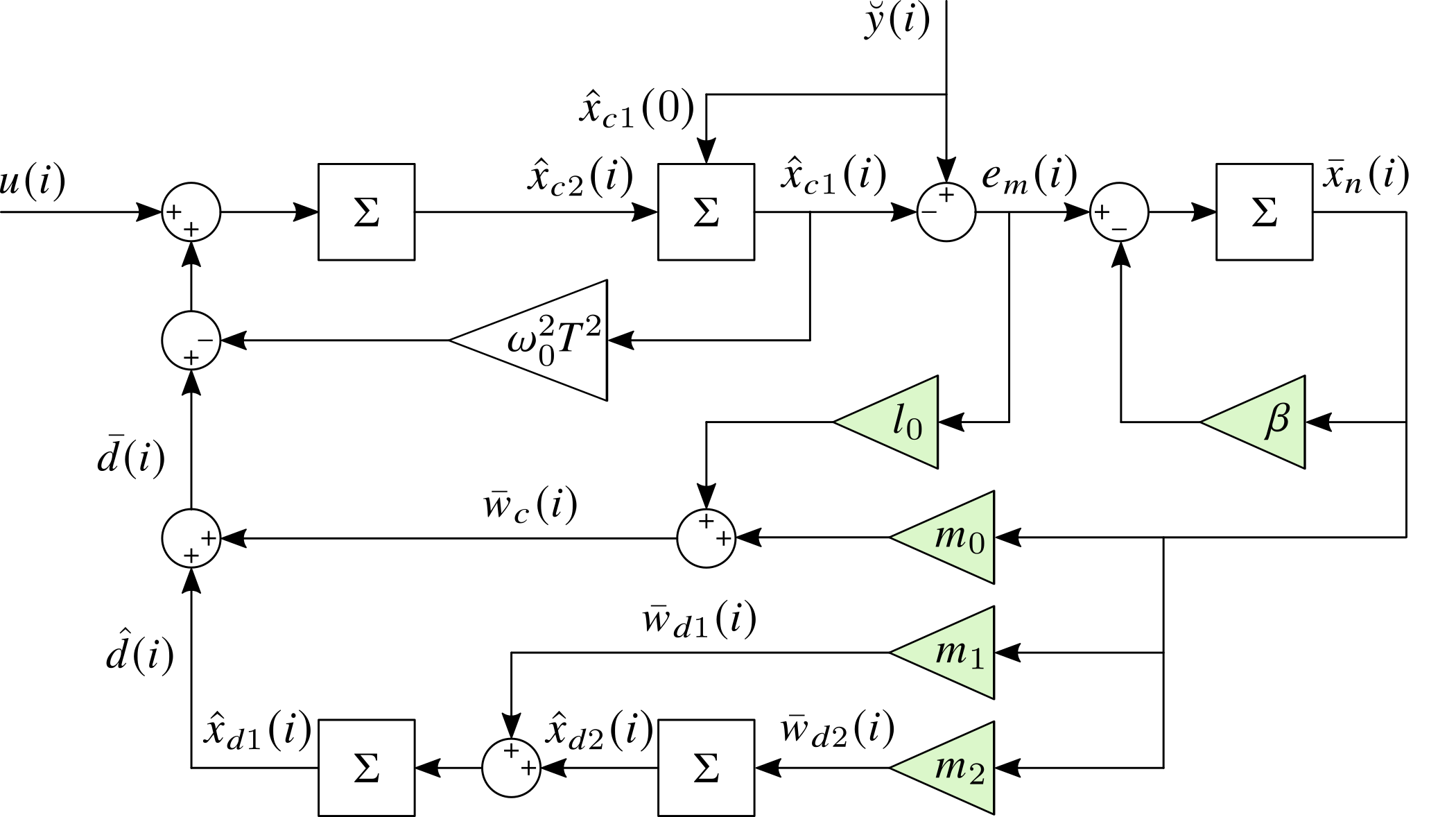
$$ \left\{\begin{aligned} & \bar{x}_n(i+1) = \left( 1-\beta \right) \bar{x}_n(i) + \tilde{y}(i) \\ & \begin{bmatrix} w_c(i) \\ w_{d1}(i) \\ w_{d2}(i) \end{bmatrix} = \begin{bmatrix} m_0 \\ m_1 \\ m_2 \end{bmatrix} \bar{x}_n(i) + \begin{bmatrix} l_0 \\ 0 \\ 0 \end{bmatrix}\tilde{y}(i) \end{aligned}\right. $$此时状态预测器共有五个状态变量,同时具备五个待调参数 $\{ \beta, \, l_0,\, m_0,\, m_1,\, m_2\}$,可以证明闭环极点任意调整,因而闭环性能可以通过参数调整来满足。该二阶系统的状态预测器环路如下图所示,五个绿色模块为待调参数。