模型嵌入控制(3):不确定性建模
被控对象模型的各种不确定性会产生模型误差而影响状态预测,为了在设计中考虑不确定性的影响,本文简要介绍鲁棒控制的核心结论,并讨论被控对象的不确定性建模。
鲁棒控制基础
鲁棒控制采用范数的形式对信号和系统进行描述,通过约束最不利情况来实现系统鲁棒性约束。不确定性的建模和考量将采用鲁棒控制的思路,因此先简要补充鲁棒控制的基础知识。
范数的引入
设 $\bm{x}(t)$ 为定义在 $[0,\,+\infty]$ 范围且能量有限的向量信号,为了节约符号,将其傅里叶变化记为 $\bm{x}(j\omega)$,$\mathcal{H}_2$ 范数定义为:
$$ \left\lVert \bm{x} \right\rVert_2^2 := \frac{1}{2\pi} \int_{-\infty}^{+\infty} \mathrm{trace} \bigl( \bm{x}^*(j\omega) \bm{x}(j\omega) \bigr) \, \mathrm{d}\omega = \int_0^{+\infty} \mathrm{trace} \bigl( \bm{x}^*(t) \bm{x}(t) \bigr) \, \mathrm{d} t $$角标 $()^*$ 表示共轭转置。后一个等号指明信号的频域积分与时域积分相等,这个关系称为怕赛瓦尔等式。
特别地,对于一维实数信号 $x(t)$,其 $\mathcal{H}_2$ 范数为:
$$ \left\lVert x \right\rVert_2^2 = \frac{1}{2\pi} \int_{-\infty}^{+\infty} \left\lvert x(j\omega) \right\rvert^2 \, \mathrm{d} \omega = \int_0^{+\infty} x^2(t) \, \mathrm{d} t $$第一个等号可以从几何上解释为信号傅里叶变换(取模的平方后)曲线下的面积,而后一个等号可以看作信号的能量。因此 $\mathcal{H}_2$ 范数实际上是对信号能量的描述。
信号的 $\mathcal{H}_2$ 范数满足三角不等式,即:
$$ \left\lVert \bm{x}_1 + \bm{x}_2 \right\rVert_2 \le \left\lVert \bm{x}_1 \right\rVert_2 + \left\lVert \bm{x}_2 \right\rVert_2 $$记 $G(j\omega)$ 为一多输入多输出稳定系统的传递函数矩阵,用 $\bar{\sigma}$ 表示矩阵的最大奇异值,则该系统的 $\mathcal{H}_\infty$ 范数定义为:
$$ \left\lVert G \right\rVert_\infty := \sup_{\omega \in \mathbb{R}} \bar{\sigma} \bigl( G(j\omega) \bigr) $$对于单输入单输出系统,$\left\lVert G \right\rVert_\infty$ 范数为传递函数最大的幅频响应,对应幅频响应的峰值。因此 $\mathcal{H}_\infty$ 范数是对系统最不利增益的描述。设 $\bm{y}(j\omega) = G(j\omega) \bm{x}(j\omega)$ 为系统的输出,不难看出:
$$ \left\lVert \bm{y} \right\rVert_2 = \left\lVert G \bm{x} \right\rVert_2 \le \left\lVert G \right\rVert_\infty \left\lVert \bm{x} \right\rVert_2 $$小增益定理
小增益定理为不确定性下的鲁棒性分析提供了数学基础。考虑将任意系统分解为如下图所示的两个稳定的子系统 $M$ 和 $\Delta$。
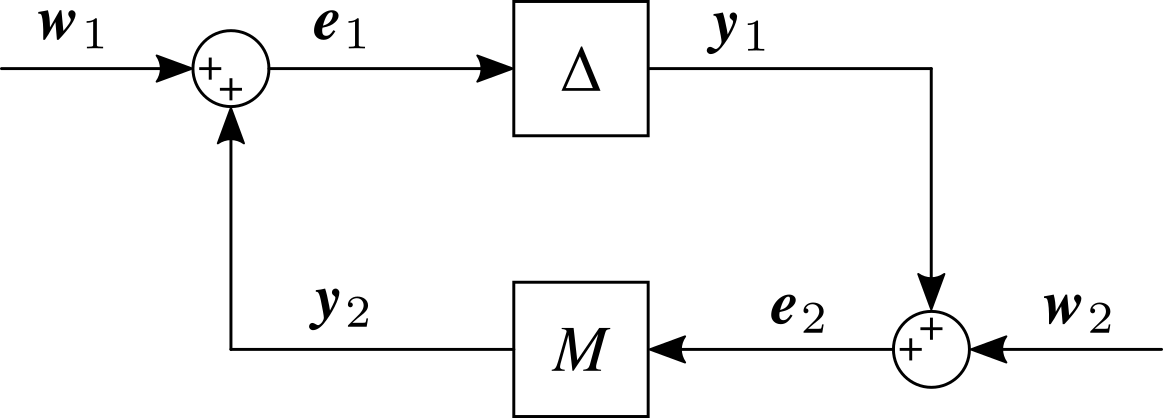
在图示输入下,容易得到:
$$ \begin{aligned} \left\lVert \bm{e}_1 \right\rVert_2 &= \left\lVert \bm{w}_1 + \bm{y}_2 \right\rVert_2 \\ &\le \left\lVert \bm{w}_1 \right\rVert_2 + \left\lVert \bm{y}_2 \right\rVert_2 \\ &\le \left\lVert \bm{w}_1 \right\rVert_2 + \left\lVert M \bm{e}_2 \right\rVert_2 \\ &\le \left\lVert \bm{w}_1 \right\rVert_2 + \left\lVert M \right\rVert_\infty \left\lVert \bm{e}_2 \right\rVert_2 \\ &\le \left\lVert \bm{w}_1 \right\rVert_2 + \left\lVert M \right\rVert_\infty \left\lVert \bm{y}_1 + \bm{w}_2 \right\rVert_2 \\ &\le \left\lVert \bm{w}_1 \right\rVert_2 + \left\lVert M \right\rVert_\infty \Bigl( \left\lVert \Delta \right\rVert_\infty \left\lVert \bm{e}_1 \right\rVert_2 + \left\lVert \bm{w}_2 \right\rVert_2 \Bigr) \end{aligned} $$当 $\left\lVert M \right\rVert_\infty \left\lVert \Delta \right\rVert_\infty<1$ 时,可知:
$$ \bm{e}_1 \le \frac{1}{1-\left\lVert M \right\rVert_\infty \left\lVert \Delta \right\rVert_\infty} \Bigl( \left\lVert \bm{w}_1 \right\rVert + \left\lVert M \right\rVert_\infty \left\lVert \bm{w}_2 \right\rVert \Bigr) $$改式说明误差 $\bm{e}_1$ 的能量有界而不会发散,闭环系统稳定。
因此我们可以得到小增益定理:对于稳定的 $M$ 和 $\Delta$,如果有:
$$ \left\lVert M \right\rVert_\infty \left\lVert \Delta \right\rVert_\infty \le \eta < 1 $$则由 $M$ 和 $\Delta$ 构成的闭环系统稳定,并记 $\eta^{-1}$ 为增益裕度。
被控对象的不确定性
在小增益定理的加持下,对于未知的 $\Delta$,我们可以将其看作最不利包络(加权函数)$W$ 与形式未知但 $\mathcal{H}_\infty$ 范数小于 $1$ 的 $\delta$ 的组合,即 $\Delta = W \delta$。于是 $M$-$\Delta$ 系统可以分解为 $MW$-$\delta$,环路稳定性可以根据 $\left\lVert MW \right\rVert_\infty$ 判断。因此,不确定性建模的核心在于其传递函数矩阵包络的确定。
参数不确定
我们再次重复 被控对象建模 所讨论的可控动态模型的状态空间方程:
$$ \left\{\begin{aligned} & \bm{x}_c(i+1) = A_c \bm{x}_c(i) + B_c \Bigl( \bm{u}(i) + \bm{h}(\bm{x}_c(i) \Bigr) + \bm{d}(i) \\ & \bm{y}(i) = C_c \bm{x}_c(i) + C_d \bm{x}_d(i) \end{aligned}\right. $$其中 $\bm{h}(\cdot)$ 为状态之间的耦合,并记 $M(z) = C_c \left( zI -A_c \right)^{-1} B_c$ 为可控动态的传递函数矩阵。
在实际设计中,我们通常将耦合分为可知的部分 $\bm{h}_{\mathrm{nom}}(\cdot)$ 和由不确定参数导致的完全未知的 $\bm{h}(\cdot)$,前者可以集成在嵌入模型中以减小模型误差,或者完全忽略以简化设计。
考虑到状态之间的耦合可能是非线性的,为了便于分析,受限考虑将耦合的影响约束在扇形有界的范围内,即寻找矩阵 $H$ 使得:
$$ -H^\mathrm{T} \bm{x}_c \le \bm{h}(\bm{x}_c) \le H^\mathrm{T} \bm{x}_c $$进一步,将状态耦合的折算到输出。使用稳定的传递函数矩阵 $\varUpsilon(z)$ 表述最不利情况,使耦合满足:
$$ \left\lVert \bm{h}(\bm{x}_c) \right\rVert_2 \le \left\lVert H^\mathrm{T} \bm{x}_c \right\rVert \le \left\lVert \varUpsilon(z) \right\rVert_\infty \left\lVert \bm{y} \right\rVert_2 $$参数不确定性对输出的影响为:
$$ \left\lVert \bm{h}_y(\bm{x}_c) \right\rVert_2 = \left\lVert M(z) \bm{h}(\bm{x}_c) \right\rVert_2 \le \left\lVert M(z) \varUpsilon(z) \right\rVert_\infty \left\lVert \bm{y} \right\rVert_2 $$我们将参数不确定性定义为:
$$ \partial H(z) := M(z) \varUpsilon (z) $$进一步根据考虑到扰动动态为:
$$ \left\{\begin{aligned} &\bm{x}_d(i+1) = A_d \bm{x}_d(i) + G_d \bm{w}_d(i) \\ &\bm{d}(i) = H_c \bm{x}_d(i) + G_c \bm{w}_c(i) \end{aligned}\right. $$如果记驱动噪声 $\bm{w} = [\bm{w}_c,\,\bm{w}_d]$ 到输出的传递函数矩阵为:
$$ D_y(z) = \begin{bmatrix} C_c & C_d \end{bmatrix} \left( zI - \begin{bmatrix} A_c & H_c \\ 0 & A_d \end{bmatrix} \right)^{-1} \begin{bmatrix} G_c & 0 \\ 0 & G_d \end{bmatrix} $$则由驱动噪声和参数不确定性对可控动态输出端的总扰动为:
$$ \bm{d}_y = D_y \bm{w} + \partial H \bm{y} $$未建模动态
在可控动态建模时会存在未建模动态,这一方面可能是因为我们对模型动态响应认识不充分,另一方面可能是人为地忽略掉部分动态以使设计变的简单。记被控对象真实的传递函数矩阵为 $P(z)$,则未建模动态可以表示为:
$$ \partial P(z) = \bigl( P(z) - M(z) \bigr) M^{-1}(z) = P(z) M^{-1}(z) - I $$于是模型误差可以写为:
$$ \tilde{\bm{y}}_m = \breve{\bm{y}} - \bm{y} = P \bm{u} + \bm{w}_m - M \bm{u} = \partial P \bm{y} + \bm{w}_m $$式中 $\bm{w}_m$ 为传感器的测量噪声。
综合上述讨论,参数不确定性和未建模动态与可控动态的关系由下图给出:
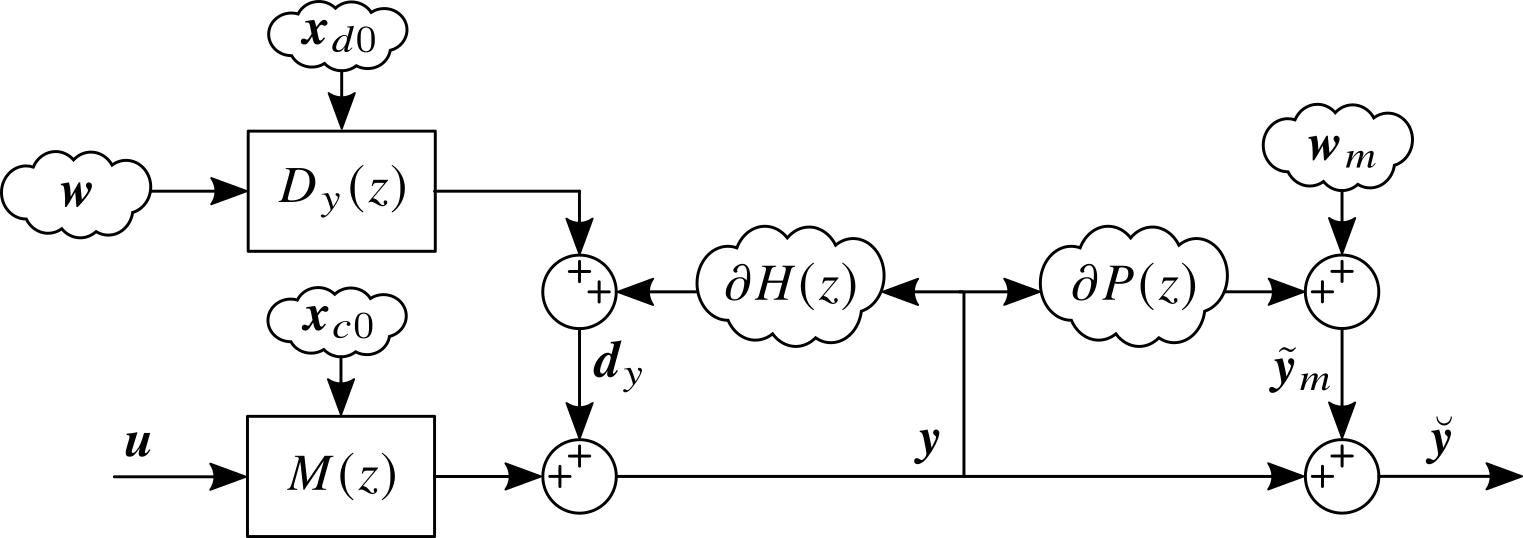
实际应用中可以使用蒙特卡洛仿真来估计 $\partial H(z)$ 和 $\partial P(z)$ 的边界供后续设计。
参考文献
- H. Kwakernaak. Robust control and H∞-optimization—Tutorial paper. Automatica. 29. 255–273. 1993.
- K. Zhou, J.C. Doyle. Essentials of Robust Control. Prentice Hall. 1998.
- J.C. Doyle, B.A. Francis, A.R. Tannenbaum. Feedback Control Theory, Courier Corporation. 1990.