模型嵌入控制(1):简介与符号约定
模型嵌入控制(EMC:Embedded Model Control)是一种基于模型的数字控制器,能够对未知的扰动进行预测与补偿,并使被控对象收敛于控制器内部的嵌入模型,因而具有很好的鲁棒性。本文将简要介绍模型嵌入控制的结构及基本原理,并对常用的符号定义进行归纳。
模型嵌入控制简介
模型嵌入控制基于状态空间进行建模与设计,当建模准确,在分离原理的加持下,闭环系统的环路设计可以分解为状态估计/预测环路和理想控制环路。模型嵌入控制以嵌入模型为核心,构建状态预测器,并基于预测的状态综合控制指令,构成完整的数字控制器。下面我们将对各个组成部分进行介绍。
被控对象与嵌入模型
基于模型的控制器设计首先需要对被控对象进行建模,在给定输入下,被控对象可能存在不可控的状态,实际建模时主要考虑其中可控状态的建模,相应的模型称为可控动态(Controllable Dynamics)。此外,区分可控动态和被控对象将有利于以后对模型误差的讨论。
如下图所示,蓝色阴影区内表示实际的被控对象,黄色阴影区内表示同时运行的数字计算单元。假设可控动态对被控对象的建模准确,并在数字计算单元内引入相同的可控动态,当两者同时接受相同的控制指令 $\bm{u}$ 时,被控对象的输出 $\bm{y}$ 应当与数字单元内可控动态的输出 $\hat{\bm{y}}$ 相同。然而,实际的被控对象会受到未知的外部扰动 $\bm{d}$ 的影响,从而使两个输出之间存在误差。如果将扰动看作被控对象的一部分,那么这一误差可以解释为被控对象建模时忽略了扰动模型而引入的,因此将其称为模型误差,定义为 $\bm{e}_m = \bm{y} - \hat{\bm{y}}$。
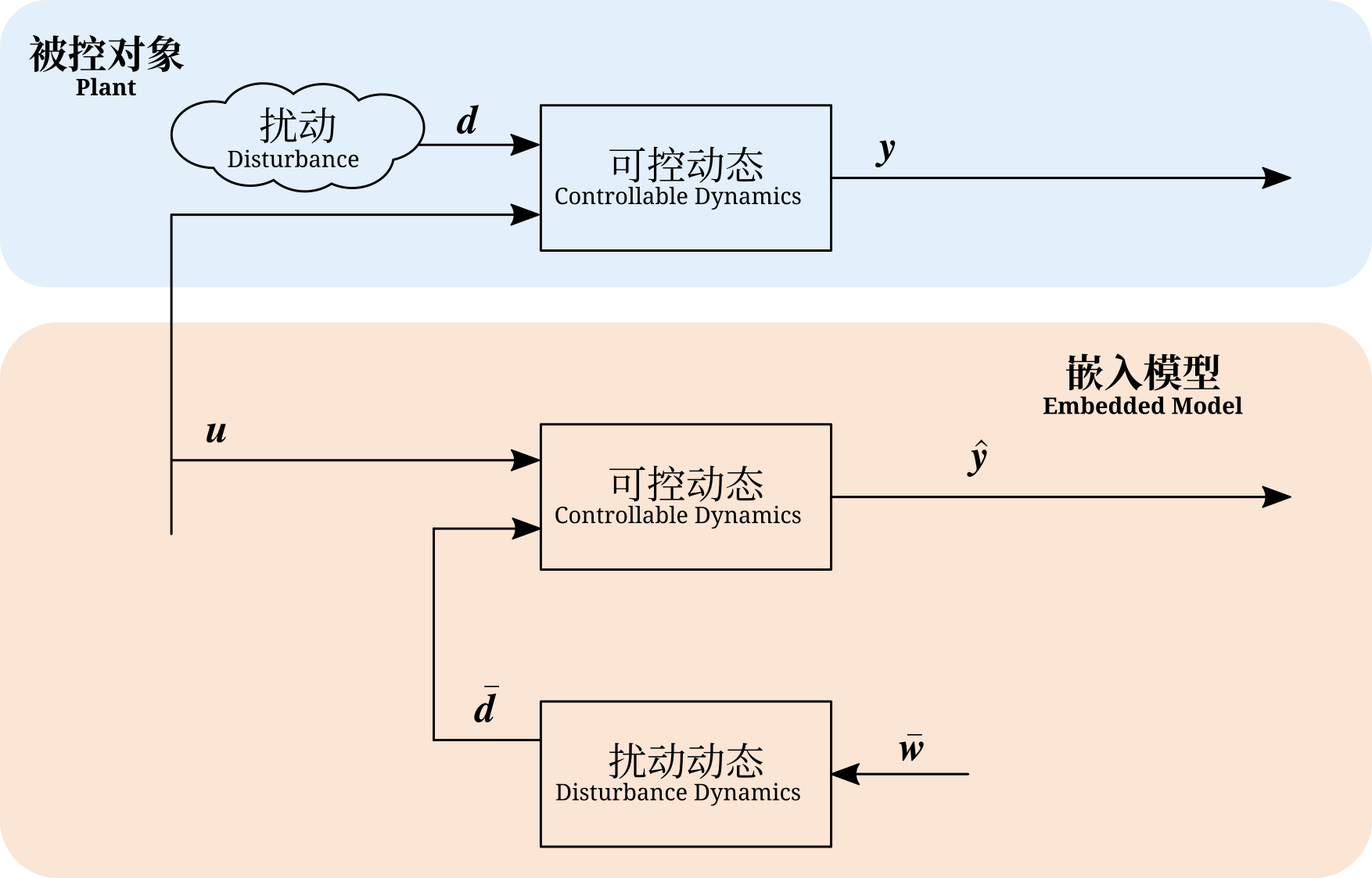
为了减小模型误差,在数字计算单元内进一步引入扰动动态(Disturbance Dynamics),与可控动态一同构成所谓的嵌入模型(Embedded Model)。扰动的建模是将扰动看作随机驱动噪声 $\bar{\bm{w}}$ 经过扰动动态后的输出。特别地,被控对象受到的扰动可以分为可预测和不可预测(完全随机)两个部分,前者可以根据扰动的特性进行建模,基于模型进行预测并通过反馈实现补偿;后者只能通过环路特性进行估计,是影响系统性能的主要因素。这将在以后状态预测器设计中详细讨论。
状态预测器
状态预测的实现依赖于对嵌入模型的驱动噪声 $\bar{\bm{w}}$ 的估计。引入噪声估计器从模型误差 $\bm{e}_m$ 中估计驱动噪声,状态预测环路的基本结构如下图黄色区域所示。
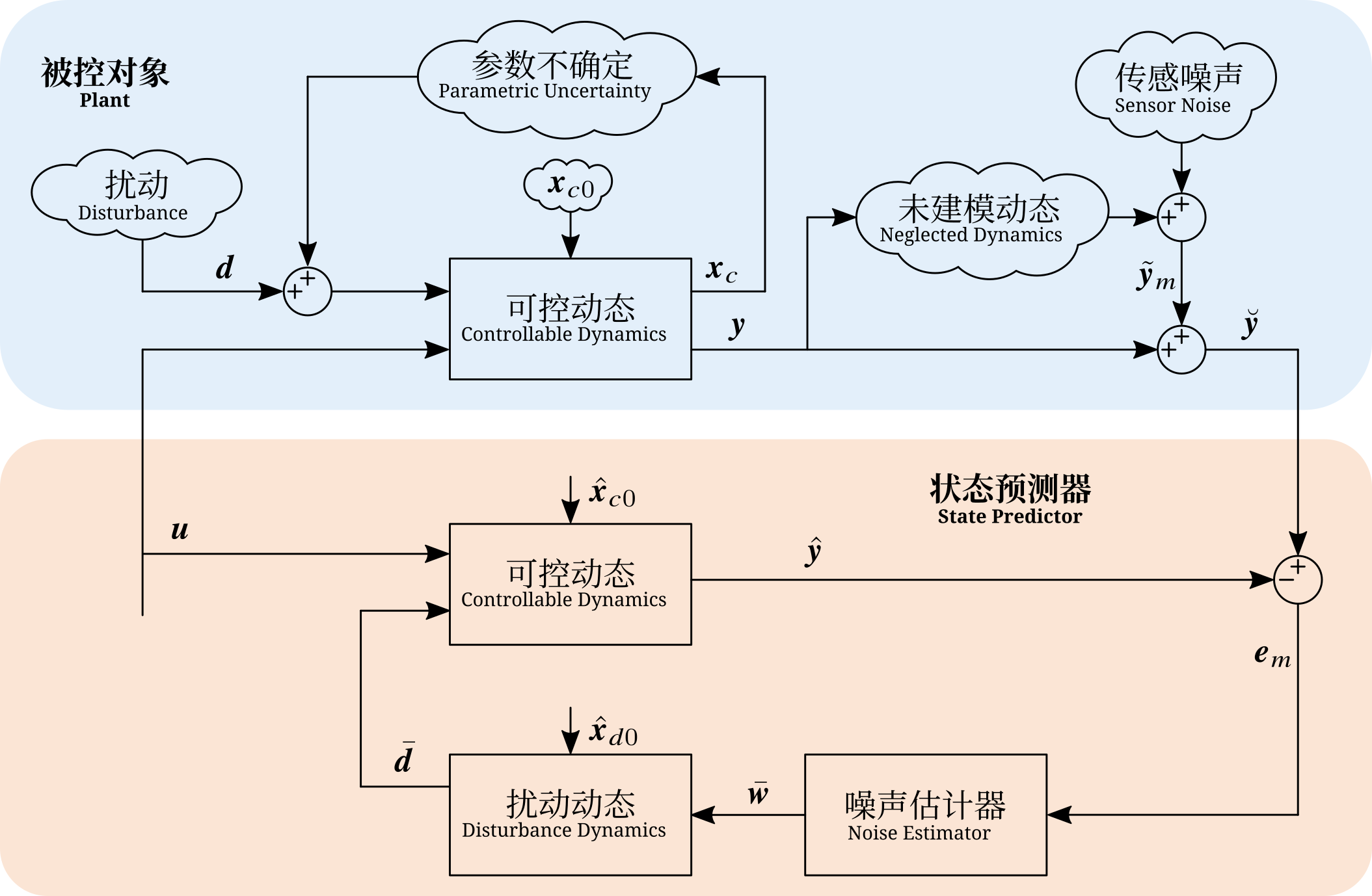
在以后的讨论中我们将指出:模型嵌入控制的设计结果能够驱动被控对象收敛于嵌入模型,换言之,完整控制环路的灵敏度函数将收敛于状态预测器。因此状态预测环路是模型嵌入控制设计的核心要素。状态预测环路的性能会受到被控对象不确定性的影响,模型嵌入控制将其归纳为四类:(1)初始状态的不确定性:被控对象的初始状态通常是未知的,相较于嵌入模型中人为给定的初始状态存在不确定性;(2)随机扰动:包括被控对象输入端的扰动以及传感噪声对输出的影响;(3)参数不确定性:被控对象的实际参数相较于可控动态建模使用的参数存在不确定性;(4)未建模动态:由于对被控对象的认识不充分,或者为了简化设计而忽略一部分特性,可控动态存在未建模动态。状态预测器的设计需要充分考虑各种不确定性带来的约束。
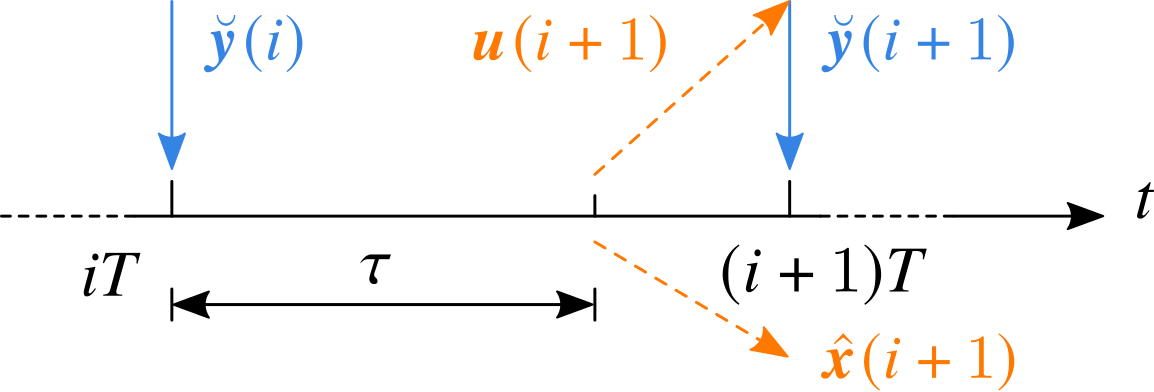
模型嵌入控制中的状态预测器(State Predictor)与一般控制器中的状态估计器(State Estimator)或着状态观测器(State Observer)具有相似的地位。考虑到数字控制存在单位延时,如下图所示。假设数字控制器的时间步长为 $T$,当其在 $iT$ 时刻接收到测量值 $\breve{\bm{y}}(i)$ 后,应当在 $\tau < T$ 时间内完成计算,并只能在 $(i+1)T$ 时刻输出。为了补偿该延时,必须对状态进行一步预测,并提前一步综合控制指令,因此我们更加倾向于使用状态预测器一词。
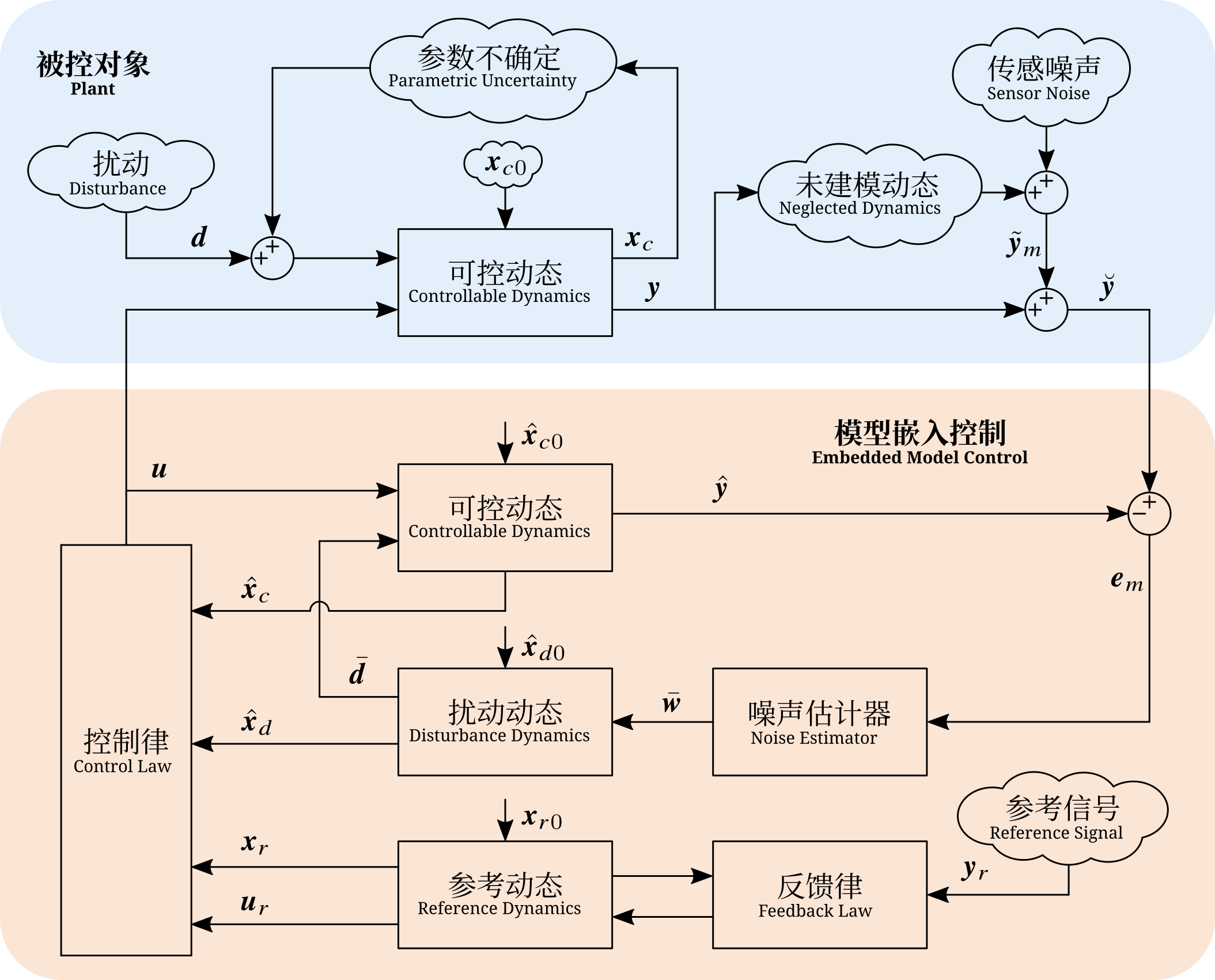
模型嵌入控制架构
控制律依据状态预测器提供的状态预测值综合得到控制指令。不失一般性地,控制律可以由三个部分构成:(1)状态反馈:这是确保闭环系统稳定的基本条件,同时用于约束随机噪声对闭环性能的影响;(2)扰动补偿:将可预测部分的扰动进行反馈与补偿有利于提高被控对象的抗扰能力;(3)参考跟随:利用参考动态和特定的反馈律构成参考发生器,可以为被控对象提供合适的参考状态和参考指令,参考动态将以状态误差的形式进入控制律以确保被控对象对参考信号进行跟随,而参考指令作为开环指令有利于改善系统的动态过程。模型嵌入控制完整的架构如下图所示。
符号约定
为了讨论的便利,本系列文章将采用以下符号约定:
- 为了不失一般性,粗体小写字母表示矢量,对应多输入多输出系统;普通小写字母表示标量;
- 相似地位的物理量采用相同的符号,但使用不同的帽子加以区分,使用的帽子有:
- (不加任何帽子):除特别定义外表示真值,通常不可知;
\breve$(\breve{*})$:测量值,对应传感器输出;\tilde$(\tilde{*})$:误差或噪声,由定义给出;\hat$(\hat{*})$:预测值,由模型给出,可用于控制律;\bar$(\bar{*})$:估计值,由反馈决定,只用于状态预测器。
- 为了排版的方便,正文中行内公式的向量均表示列向量,如 $[\bm{w}_c ,\, \bm{w}_d]$。作为对比,其严格的数学写法应当为 $[\bm{w}_c^\mathrm{T},\,\bm{w}_d^\mathrm{T}]^\mathrm{T}$。
为了便于系数矩阵的检索,通常情况下,可控动态的线性状态空间方程写为:
$$ \left\{ \begin{aligned} &\bm{x}_c(i+1) = A_c \bm{x}_c(i) + B_c \bm{u}(i) + \bm{d}(i) \\ &\bm{y}(i) = C_c \bm{x}_c(i) + C_d \bm{x}_d(i) \end{aligned} \right. $$扰动动态的状态空间方程为:
$$ \left\{ \begin{aligned} & \bm{x}_d(i+1) = A_d \bm{x}_d(i) + G_d \bm{w}_d(i) \\ & \bm{d}(i) = H_c \bm{x}_d(i) + G_c \bm{w}_c(i) \end{aligned} \right. $$在此约定的基础上,归纳将要用到的符号列表如下:
| 分类 | 符号 | 说明 |
|---|---|---|
| 被控对象 | $\bm{x}_c$ | 可控动态的状态变量 |
| $\bm{x}_d$ | 扰动动态的状态变量 | |
| $\bm{w}_c$ | 可控动态的随机扰动 | |
| $\bm{w}_d$ | 扰动动态的驱动噪声 | |
| $\bm{w}_m$ | 传感器的测量噪声 | |
| $\bm{u}$ | 被控对象的控制指令 | |
| $\bm{d}$ | $= H_c \bm{x}_d + G_c \bm{w}_c$ 可控动态受到的总扰动 | |
| $\bm{y}$ | 被控对象的输出 | |
| $\breve{\bm{y}}$ | 被控对象输出的测量值 | |
| 状态预测器 | $\hat{\bm{x}}_c$ | 嵌入模型中可控动态模型的状态变量 |
| $\hat{\bm{x}}_d$ | 嵌入模型中扰动动态模型的状态变量 | |
| $\bar{\bm{x}}_n$ | 噪声估计器的状态变量 | |
| $\bar{\bm{w}}_c$ | 可控动态随机噪声的估计值 | |
| $\bar{\bm{w}}_d$ | 扰动动态驱动噪声的估计值 | |
| $\bar{\bm{d}}$ | $= H_c \hat{\bm{x}}_d + G_c \bar{\bm{w}}_c$ 总外扰的估计值 | |
| $\hat{\bm{d}}$ | $= H_c \hat{\bm{x}}_d$ 可依据扰动模型进行预测的扰动 | |
| $\hat{\bm{y}}$ | 嵌入模型的输出 | |
| 参考发生器 | $\bm{x}_r$ | 可控动态状态的参考值 |
| $\bm{u}_r$ | 参考控制指令 | |
| $\bm{y}_r$ | 被控对象输出的参考值 | |
| 误差 | $\tilde{\bm{x}}_c$ | $=\bm{x}_c - \hat{\bm{x}}_c$ 可控动态的状态预测误差 |
| $\tilde{\bm{x}}_d$ | $=\bm{x}_d - \hat{\bm{x}}_d$ 扰动动态的状态预测误差 | |
| $\tilde{\bm{x}}_r$ | $=\bm{x}_c - \bm{x}_r + Q\bm{x}_d$ 被控对象状态的跟踪误差 | |
| $\tilde{\bm{y}}_m$ | $=\breve{\bm{y}}-\bm{y}$ 被控对象的模型误差 | |
| $\tilde{\bm{y}}$ | $=\bm{y} - \hat{\bm{y}}$ 被控对象输出的预测误差 | |
| $\tilde{\bm{y}}_r$ | $=\bm{y} - \bm{y}_r$ 被控对象输出的跟踪误差 | |
| $\bm{e}_m$ | $=\breve{\bm{y}} - \hat{\bm{y}}$ 测得的模型误差 | |
| $\bm{e}_r$ | $=\hat{\bm{x}}_c - \bm{x}_r + Q \hat{\bm{x}}_d$ 测得的跟踪误差 |
参考文献
- E. Canuto, C. Novara, D. Carlucci, et al. Spacecraft Dynamics and Control: The Embedded Model Control Approach. Butterworth-Heinemann. 2018.
- E. Canuto. Embedded Model Control: Outline of the theory. ISA Transactions. 2007(46). 363–377.
- E. Canuto, C. Novara, L. Colangelo. Embedded model control: Reconciling modern control theory and error-based control design. Control Theory Technol. 2018(16). 261–283.