信号的微分

数字信号处理中经常会用到微分，典型的例子就是数字 PID 控制器中的微分环节。然而理想的微分是不存在的，即使存在，其对高频噪声的放大也约束了它的实际应用。这篇文章我们将讨论并对比一些常见的微分算法。

从数值差分聊起

对于数字信号，最简单的微分方式莫过于使用后向差分对微分近似，设采样时间间隔为 $T_s$（采样率为 $f_s = \frac{1}{T_s}$），传递函数为：

$$H(z) = \frac{1}{T_s} \left( 1 - z^{-1} \right)$$

其幅频响应为：

$$ \begin{aligned} \left| H \left(\mathrm{e}^{\mathrm{j}\omega} \right) \right| &= \left| \left. H\left(z\right) \right|_{z=\mathrm{e}^{\mathrm{j}\omega T_s}} \right| \\ &= \frac{1}{T_s} \left| 1 - \mathrm{e}^{-\mathrm{j}\omega T_s} \right| \\ &= \frac{1}{T_s}\left| 1 - \left( \cos\omega T_s - \mathrm{j} \sin \omega T_s\right) \right| \\ &= \frac{1}{T_s} \sqrt{ \left( 1 - \cos \omega T_s \right)^2 + \sin^2 \omega T_s } \\ &= \frac{1}{T_s} \sqrt{ 2 - 2 \cos \omega T_s } \\ &= \frac{1}{T_s} \sqrt{4 \sin^2 \frac{\omega T_s}{2}} \\ &= 2 f_s \sin \pi\frac{f}{f_s} \approx 2\pi f = \left| s \right| \quad (f \ll f_s) \end{aligned} $$

可见数值差分与理想微分 $s$ 的传递函数存在差异，只有采样率远大于被微分信号的频率时才可以用差分代替微分。

除此之外，在 Nyquist 采样定理的约束，即 $f < \frac{1}{2} f_s$ 条件下，数值差分的幅频响应是单调递增的，这意味着信号中的高频噪声会被数值差分所放大，很容易导致时域的微分信号淹没在高频噪声之中。

为了说明数值差分对噪声的放大，考察下面的信号：左图橙色曲线为理想的单频信号，蓝色曲线引入了白噪声并将其假设为实际采集到的信号，采样率设置为 $f_s = 200 , \mathrm{Hz}$ 。右图中蓝色曲线是数值差分的结果，可见微分信号完全淹没在高频噪声之中，单独的数值差分难以直接使用；配合低通滤波后的输出为橙色曲线所示，可以看到微分信号；理想的微分信号如绿色曲线所示。

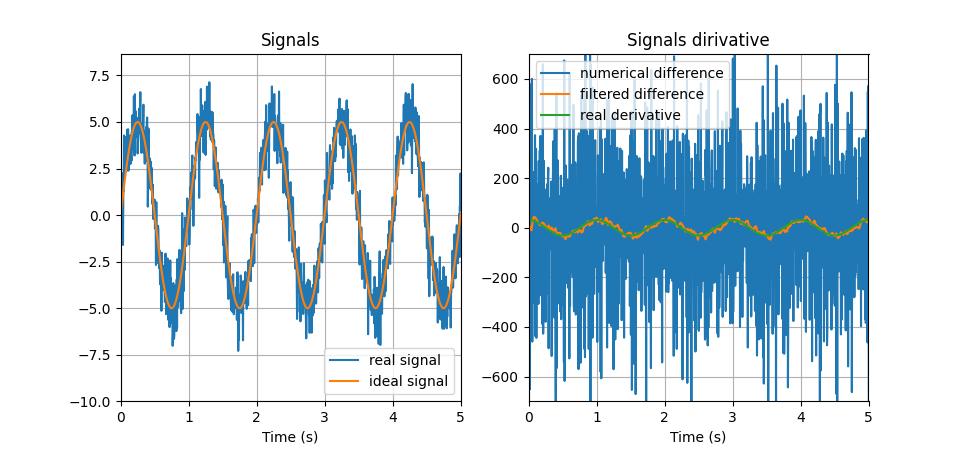
虽然可以使用滤波器将数值差分后放大的高频噪声衰减下去，但是在实际应用，尤其是设计定点化数据时应当注意增益增益分配，以免导致数据溢出。例如可以考虑差分后先进行滤波，再乘以 $\frac{1}{Ts}$ 系数。当然，滤波器会引入延时，实际使用时应当考虑这一影响；如果只是对采集到的信号进行处理，可以使用非因果的零相位滤波，以避免滤波延时的影响。

从模拟微分中找找灵感

既然数值差分存在高频噪声放大的问题，不妨看看模拟微分器是如何实现的，或许能够从中找的一些新的灵感。

模拟微分器从导数的定义出发（假设信号连续且光滑）：

$$f'(x) = \lim_{T \to 0 } \frac{f(x+T)-f(x)}{T} = \lim_{T \to 0 } \frac{f(x)-f(x-T)}{T}$$

可见，除了减法和除法，构造模拟微分器的关键就是产生足够小的延时。考虑延时的 Laplace 变换为 $\mathrm{e}^{-s T}$ ，则上式对应的传递函数可以写为

$$H_1(s) = \frac{1}{T} \left( 1- \mathrm{e}^{-s T}\right) \approx \frac{1}{T} \left( 1- \frac{1}{1+sT}\right) = \frac{s}{Ts+1}$$

上式的近似是取了延时的一阶 Pade 展开，最终的结果具有高通滤波器的形式。因此我们可以这么来看：分子的 $s$ 产生主要的微分效应，而分母的 $Ts+1$ 则用来约束高频增益，使高频噪声不被放大。显然，这种微分器是以牺牲工作带宽为代价的。

反正已经牺牲了工作带宽，有没有可能对高频噪声做进一步的抑制呢？当然是可以的，假设信号的导数也具有连续性，则：

$$f'(x) = \lim_{T_1 \to 0 } f'(x-T_1) = \lim_{T_1 \to 0 } \lim_{T_2 \to 0} \frac{f(x-T_1)-f(x-T_2)}{T_2 - T_1}$$

同样在一阶 Pade 近似下，得传递函数：

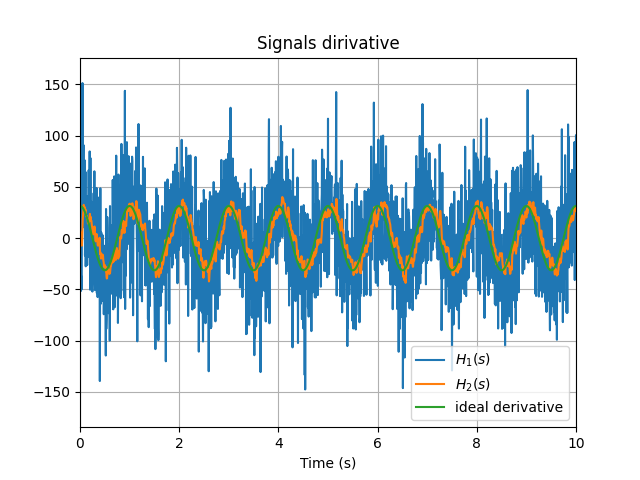
$$ \begin{aligned} H_2(s) &= \frac{1}{T_2-T_1} \left( \mathrm{e}^{-s T_1} - \mathrm{e}^{-s T_2} \right) \\ &\approx \frac{1}{T_2-T_1} \left( \frac{1}{T_1 s + 1} - \frac{1}{T_2 s + 1}\right) \\ &= \frac{s}{T_1T_2 s^2 + (T_1+T_2)s +1} \end{aligned} $$

这是一个带通滤波器！其幅频响应的"左侧"构成微分的功能，而"右侧"能够高频噪声进行抑制。下图展示了这两种微分器的效果。

进一步，考察带通滤波形式微分器如下所示的结构框图：

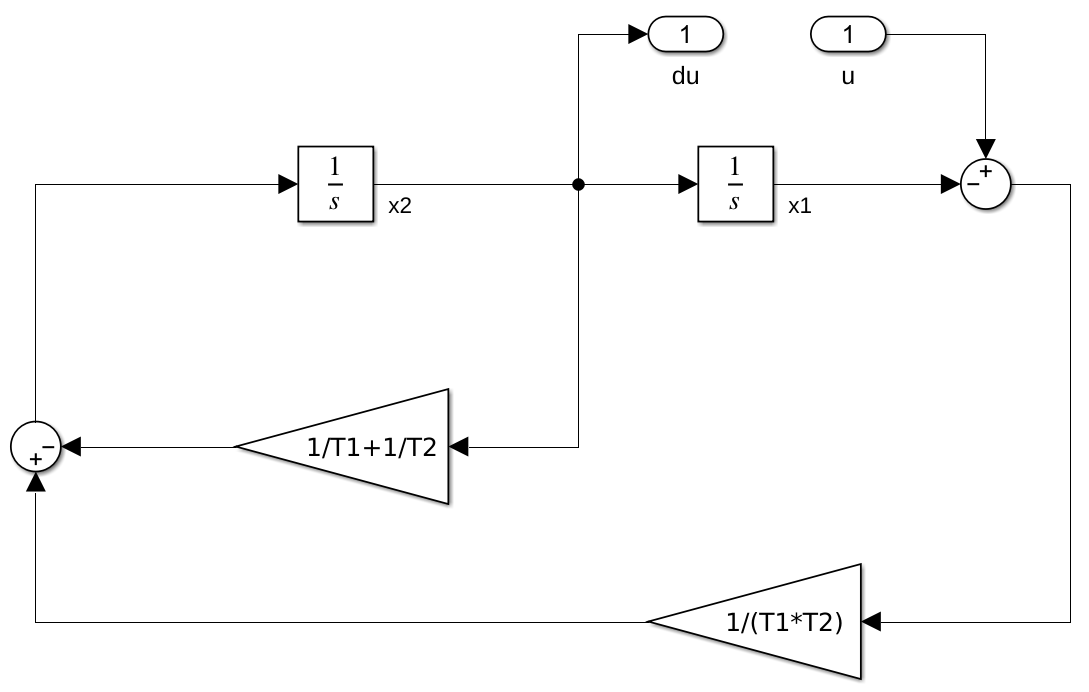
可以这么理解：构造串联积分作为"被控对象"，使其输出跟随系统的输入，即 $x_1 = u$；通过理想的状态反馈确保环路稳定，那么第二个状态量 $x_2 = \dot{x}_1$ 就是输入信号的微分。这实际上就是控制理论中的状态观测器！

跟踪微分器

从模拟微分器中已经学到：利用状态观测器跟踪输入信号，那么各状态量就分别对应输入信号的各阶导数（不再局限于一次微分），因此这种微分器称为跟踪微分器。跟踪微分器的环路稳定性可以通过反馈控制来保证，因此具有以下通用的形式：

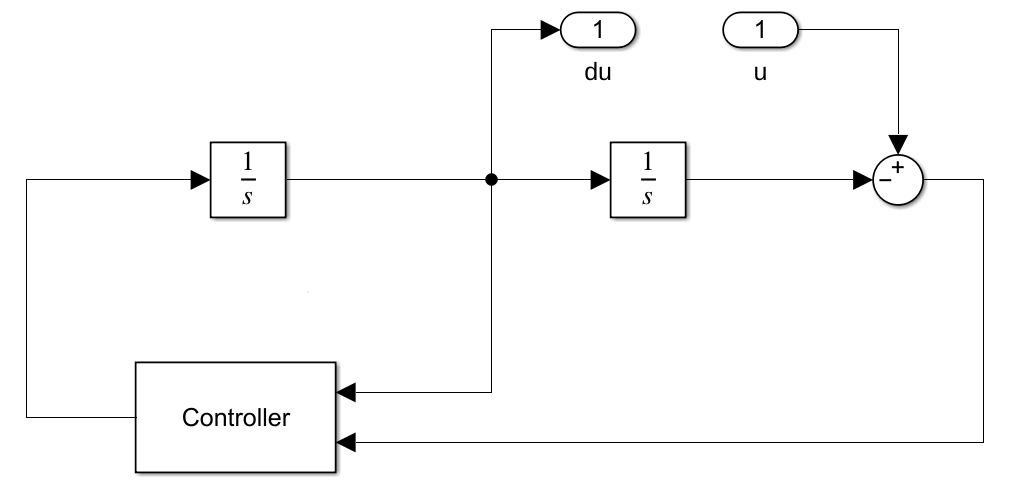
特别地，如果使用 相图与砰砰控制 所讨论的砰砰控制来稳定环路，就构成了韩京清老师所定义的跟踪微分器。下图展示了这种跟踪微分器的微分效果。

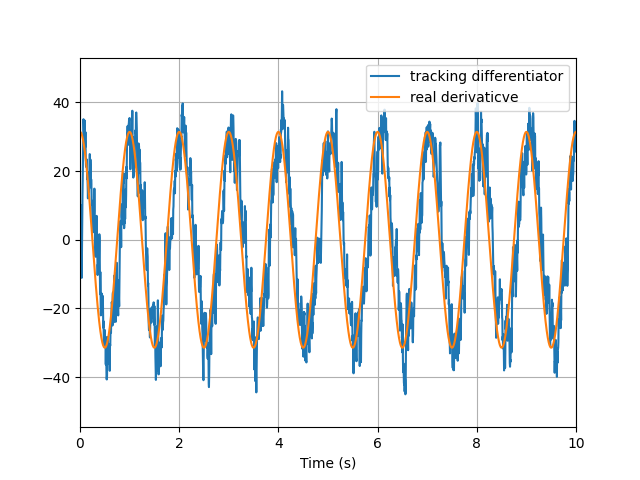
从控制的角度来看，完全可以使用其他控制器以达到对高频噪声更高阶次的抑制，这里就不再过多讨论了。

写在最后

本文仅介绍了几种常用的微分器及其实现方法，由于各形式下微分器的参数不同，并可以自由设计，故没有将这几种微分器合在一起对比，而且示例的微分器参数也未必是最优的。相关的仿真文件我放在了 GitHub 仓库，有兴趣的小伙伴可以自行取阅。

参考文献

1. 韩京清, 自抗扰控制技术: 估计补偿不确定因素的控制技术. 国防工业出版社. 2008.