相图与砰砰控制
砰砰控制(Bang Bang Control)是一种使误差收敛速度最快的最优控制,对于二阶系统,可以借助相图来完成。本文介绍相图并据此实现砰砰控制。
相图
相图(Phase Portrait)也称相轨迹,是以各状态为坐标,由状态轨迹绘制而成的图。例如,质量为 $m$,刚度为 $K$ 弹簧的状态空间方程为
$$ \left\{ \begin{aligned} \dot{x}_1 &= x_2 \\ \dot{x}_2 &= -\frac{K}{m} x_1 + \frac{1}{m} F \end{aligned} \right. $$当外力 $F=0$,弹簧从某一初始位置自由释放时,质量块会在平衡位置来回震荡,其相图如下图所示
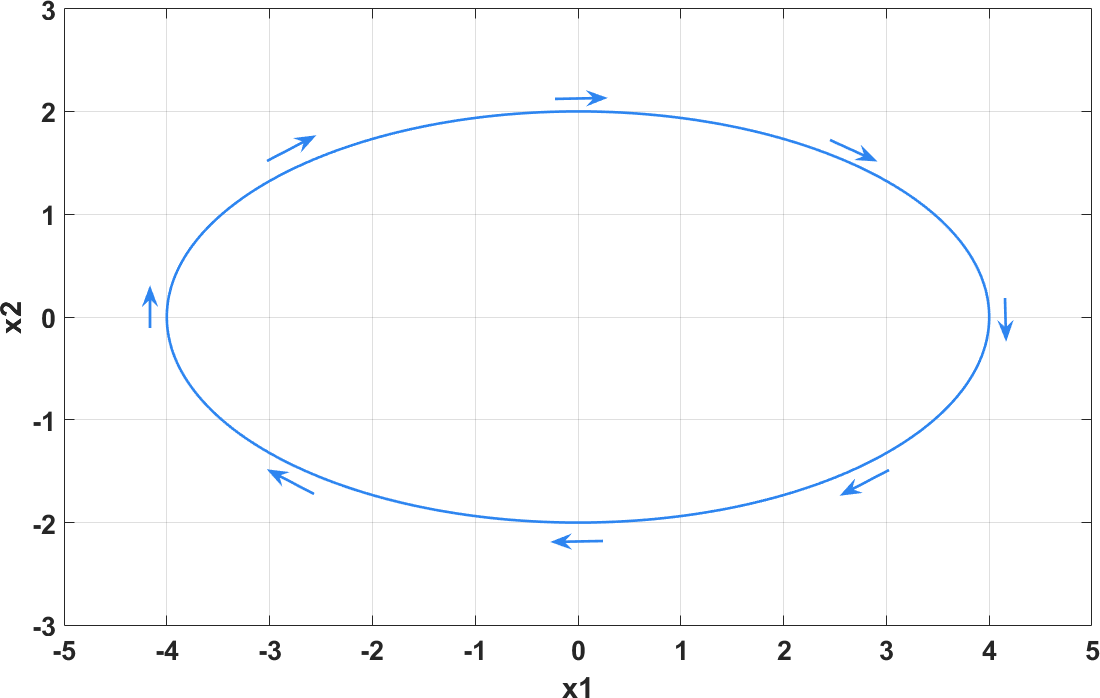
相图表示了系统状态随时间的发展趋势,在分析系统动态时非常有用。此外,bilibili 的 up 主 DR_CAN 在他的一期视频里 利用相图分析了爱情,很有意思,有兴趣的朋友可以看一下。
砰砰控制
砰砰控制(Bang Bang Control)又称开关控制,它的控制信号非正即负,系统响应要么全力加速要么全力减速,因而是一种最速控制。以二阶系统为例,为了确定控制信号(加速度)变号的时刻,考察系统在 $u=u_{\rm max}$ 和 $u=-u_{\rm max}$ 时的相图,如下图所示(设 $u_{\rm max}=1$ )
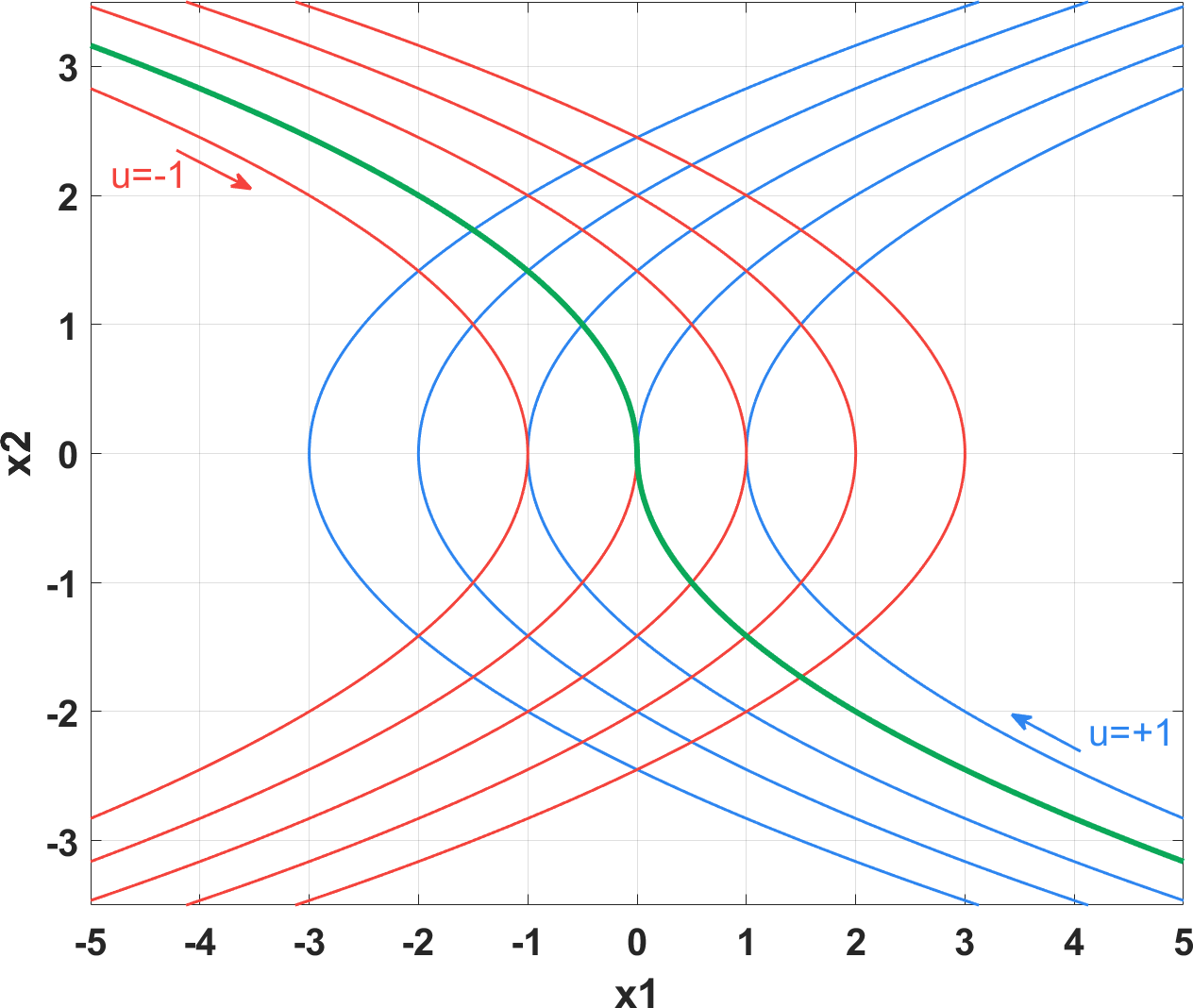
图中,蓝色曲线代表在某状态处施加正向最大控制量时系统状态的轨迹,其由第四象限拐向第一象限;红色曲线为施加负向最大控制量时状态的轨迹,由第二象限拐向第三象限。可见,存在一个临界的曲线,如图中绿色曲线所示,当初始状态在该曲线上方时,只要施加负向控制量可使状态回到绿色曲线,反之只要施加正向控制量即可回到绿色曲线。因此这个绿色的曲线就是控制信号的切换曲线。
临界曲线的解析式分别对应从原点处分别按 $u = \pm u_{\rm max} = \pm 1$ 施加控制所形成的状态轨迹,其表达式为
$$x_1 + \frac{x_2 |x_2|}{2u_{\rm max}} = 0$$因而控制信号可根据当前状态来确定
$$u = -u_{\rm max} \operatorname{sign}\left( x_1 + \frac{x_2 |x_2|}{2u_{\rm max}} \right)$$设系统初始状态 $x_1=-2,, x_2=3$ ,控制过程的状态轨迹如下图紫色曲线所示
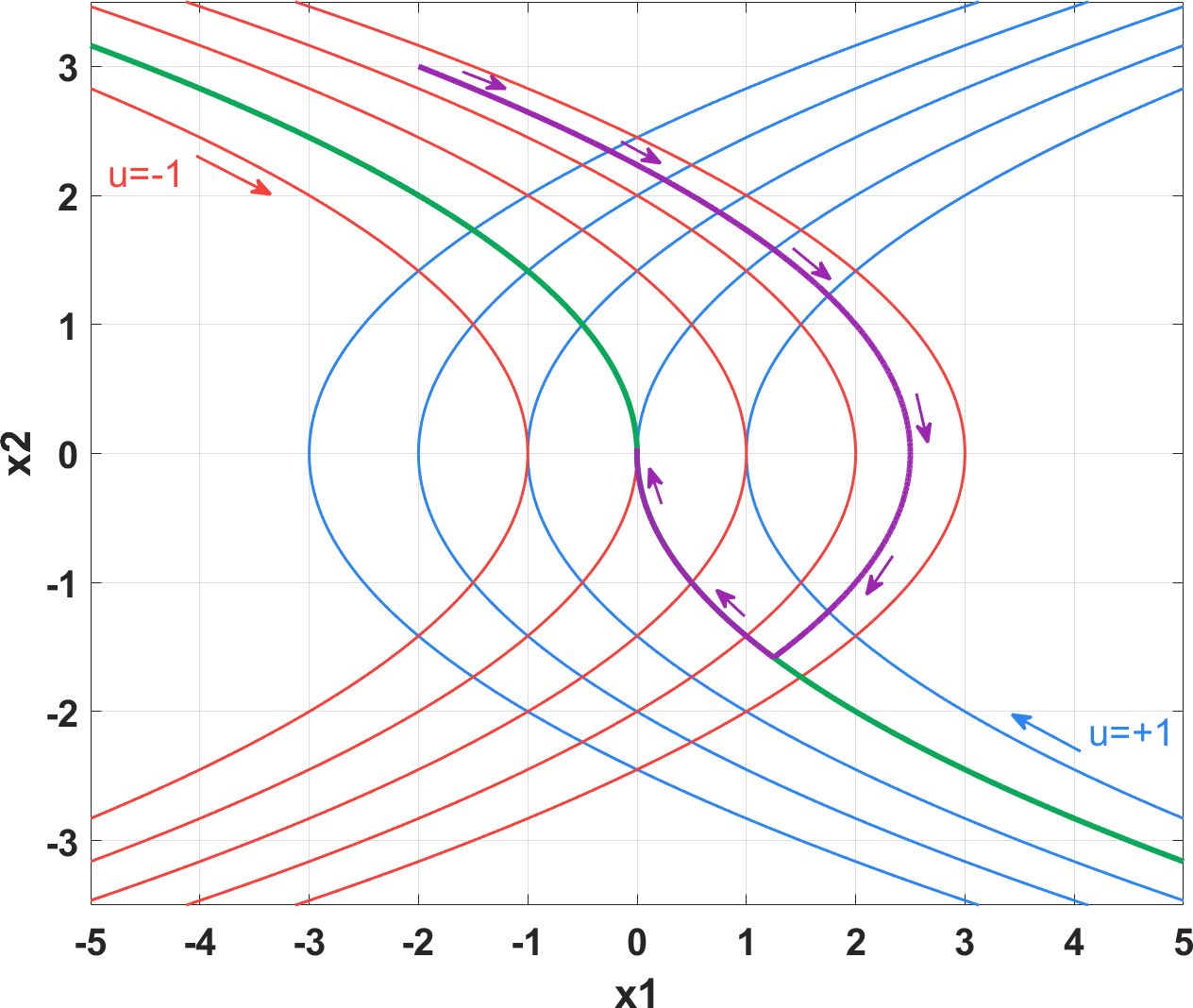
理想情况下,控制信号 $u$ 最多只需要一次切换就能达到控制效果,而实际的数字控制器中,离散状态的时间间隔限制了状态不可能正好达到相图的原点,状态轨迹会在原点附近出现高频"颤振",如下图所示。相应地,控制信号不断进行正负切换,就像乒乓球来回碰撞,砰砰控制也因此得名。
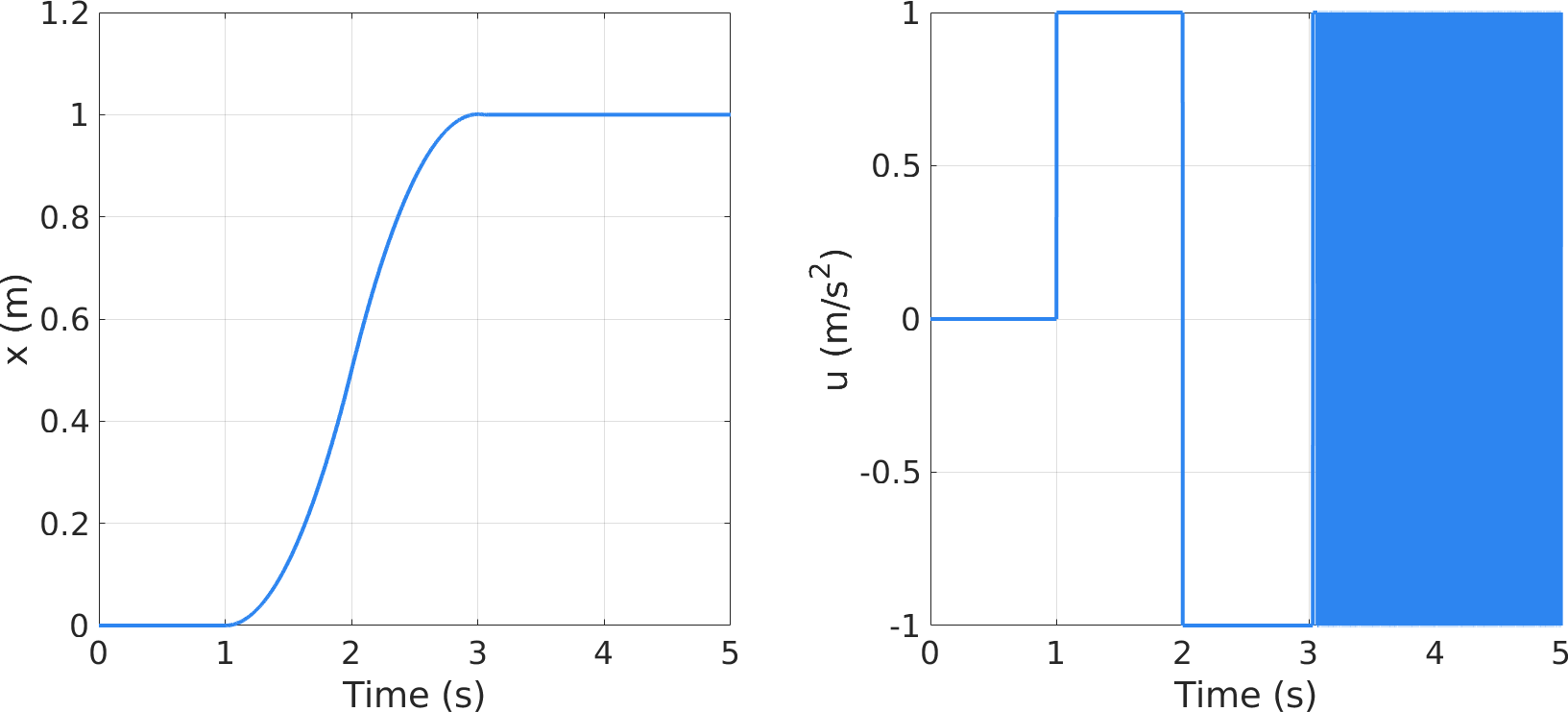
砰砰控制的高频颤振使其在实际应用中受到限制,为了解决这个问题,韩京清老师基于离散时间模型对控制信号进行了改进,提出了如下算法:
$$ \mathrm{fhan} = \left\{ \begin{aligned} & a_0 = h x_2 \\ & d = r h^2 \\ & y = x_1 + a_0 \\ & a_1 = \sqrt{d \left( d+ 8\left| y \right| \right)} \\ & a_2 = a_0 + \operatorname{sign}\left( y \right) \frac{a_1-d}{2} \\ & s_y = \frac{1}{2} \left[ \operatorname{sign}\left( y+d \right) - \operatorname{sign}\left( y-d\right)\right] \\ & a = \left( a_0 + y - a_2 \right) s_y + a_2 \\ & s_a = \frac{1}{2} \left[ \operatorname{sign}\left( a+d \right) - \operatorname{sign}\left( a-d\right)\right] \\ & \mathrm{fhan} = -r \left[ \frac{a}{d} - \operatorname{sign}\left( a \right)\right] s_a - r \operatorname{sign}\left( a \right) \end{aligned}\right. $$式中, $r=u_{\rm max}$ 为控制器输出的最大控制信号,值越大响应越快,闭环的带宽也越大。 $h$ 为采样时间,实际使用时可取独立于 $h$ 的变量 $h_0 =n h$ 以抑制高频噪声,即 $u = \operatorname{fhan}\left( x_1, , x_2, , r, , h_0 \right)$。采用这种算法,砰砰控制不再出现高频颤振,如下图所示。
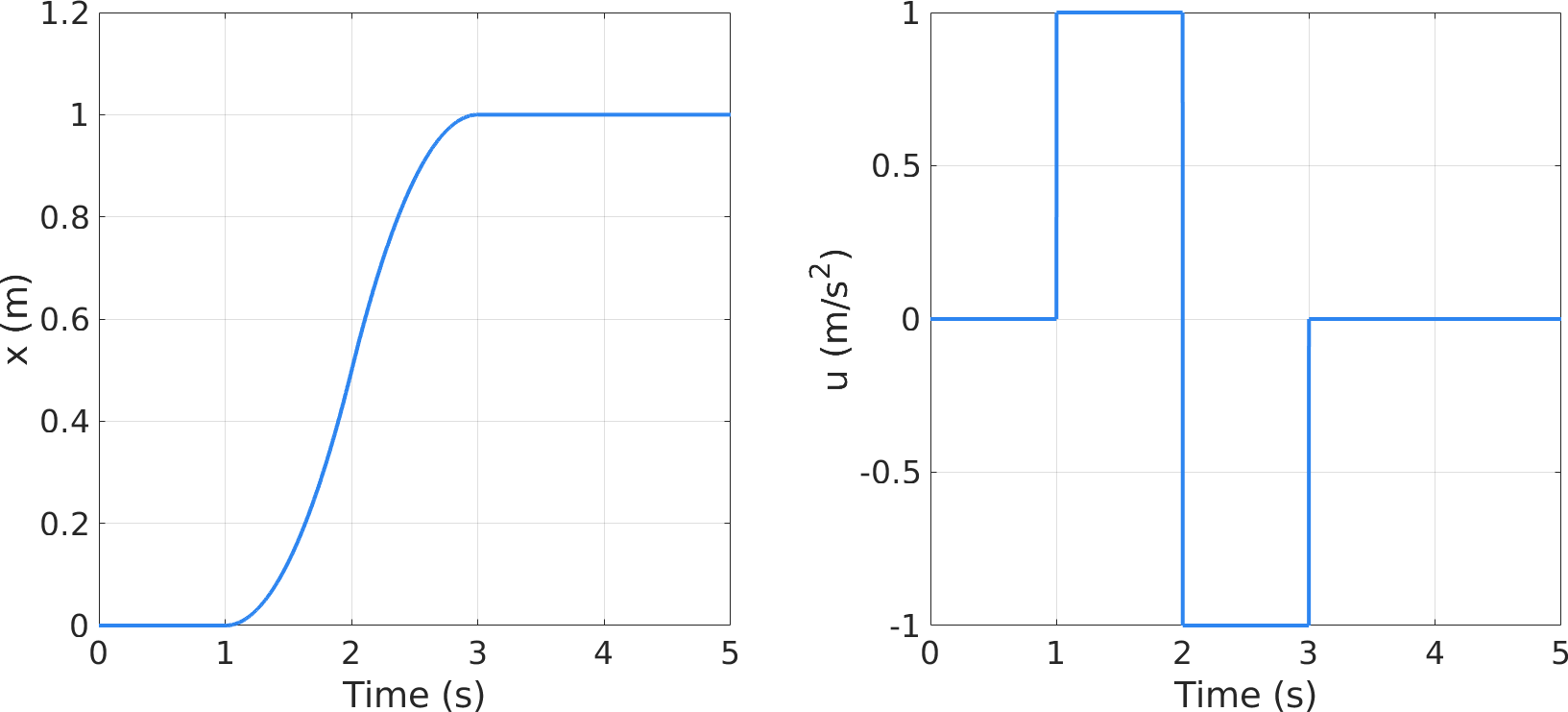
fhan 最优综合下的砰砰控制参考文献
- G.F. Franklin, J. D. Powell, A. Emami-Naeini. Feedback Control of Dynamic Systems. 7th ed. 2014. p673-676.
- 韩京清, 自抗扰控制技术: 估计补偿不确定因素的控制技术. 国防工业出版社. 2008. p107.