使用反步法设计非线性控制器

反步法（Backstepping）通过拼凑李雅普诺夫函数得到控制律，可用于非线性被控对象的控制器设计。本文是对 DR_CAN 系列视频的学习，并以一个开环不稳定的非线性系统为例进行设计与仿真。

反步法基本思路

为了使用李雅普诺夫函数判定系统稳定性，首先做如下定义：

对于标量函数 $V(\bm{x})$，若有

• $V(\bm{x}) = 0, \ \bm{x}=0$
• $V(\bm{x}) > 0,\ \bm{x}\ne 0$

则称 $V(\bm{x})$ 为正定函数。如果 $\bm{x}\ne 0$ 时 $V(x)\ge 0$，则称之为半正定函数。类似地，如果 $\bm{x}\ne 0$ 时 $V(x) < 0$ 则将其称为负定函数；如果 $V(x) \le 0$ 则为半负定函数。

非线性系统的稳定性可以通过李雅普诺夫直接法进行判定：如果一个关于所有状态的函数 $V(\bm{x})$ 是正定的，其导数 $\dot{V}(\bm{x})$ 为半负定的，则该函数为李雅普诺夫函数，且对应的系统稳定。进一步，如果 $\dot{V}(\bm{x})$ 是负定的，则系统渐进稳定。

反步法的基本思路是逐级构造关于误差的正定函数，通过误差动态模型将该正定函数的导数凑成负定函数，从而获得控制律的具体表达，使系统满足稳定性需求。

示例与公式推导

假设现有非线性负刚度弹簧系统，其状态空间方程表述为

$$ \left\{ \begin{aligned} \dot{x} &= v \\ \dot{v} &= a x^2 + u \end{aligned} \right. $$

其中 $u$ 为控制命令。设控制的目标是使位移 $x$ 跟随参考位移 $x_r$，不失一般性地，控制指令应当是状态和参考的函数，即 $u=f(x,v,x_r)$。反步法的目标就是设计非线性控制律 $f(\cdot)$ 来实现参考信号的跟随。需要说明的是，参考信号可以通过多种手段给出，因此 $x_r$ 及其导数均可以认为是已知的，可直接用于构成控制律。

控制器设计以误差收敛为目标，首先定义位移跟踪误差，并构造第一级李雅普诺夫函数

$$ \left\{ \begin{aligned} e_1 &= x - x_r \\ V_1 &= \frac{1}{2} e_1^2 > 0, \quad (e_1 \ne 0) \end{aligned} \right. $$

$V_1$ 在 $e_1\ne 0$ 时均为正值，即为正定的。$e_1$ 渐进稳定的条件是 $\dot{V}_1$ 是负定，考虑

$$ \dot{V}_1 = e_1 \dot{e}_1 = e_1 \left( v - \dot{x}_r \right) $$

为了将上式凑成负定函数，可以让 $v-\dot{x}_r = -K_1 e_1$，将该需求进一步分解为使速度的跟踪误差收敛：

$$ v - \dot{x}_r = -K_1 e_1 \rightarrow \left\{ \begin{aligned} v_r &= \dot{x}_r - K_1 e_1 \\ e_2 &= v-v_r = 0 \end{aligned} \right. $$

此时将需求从一个误差收敛扩展到了两个误差收敛，相应的李雅普诺夫函数可选取为

$$ V = \frac{1}{2} e_1^2 + \frac{1}{2}e_2^2 $$

显然它是正定的。再次考虑其导数

$$ \begin{aligned} \dot{V} &= e_1 \dot{e}_1 + e_2 \left( ax^2 + u - \left( \ddot{x}_r - K_1 \dot{e}_1 \right) \right) \\ &= e_1 \left( v - \dot{x}_r \right) + e_2 \left( ax^2 + u -\ddot{x}_r + K_1 \left( v-\dot{x}r \right) \right) \\ &= e_1 \left(-K_1 e_1 + e_2 \right) + e_2 \left( ax^2 + u -\ddot{x}_r + K_1 \left( v-\dot{x}_r \right) \right) \\ &= -K_1 e_1^2 + e_2 \left( e_1 + ax^2 + u -\ddot{x}_r + K_1 \left( v-\dot{x}_r \right) \right) \end{aligned} $$

注意，在第三行我们只将第一项的 $\dot{e}_1$ 进行了替换： $\dot{e}_1 = v-\dot{x}_r = v_r + e_2 - \dot{x}_r = -K_1e_1 + e_2$ ，这是第一次凑李雅普诺夫函数的期望；而第二项没有作此替换，是为了第二次凑负定函数。也就是说，反步法是逐级将函数凑成负定形式。显然，如果希望 $\dot{V}$ 是负定的，可以使

$$ e_1 + ax^2 + u -\ddot{x}_r + K_1 \left( v-\dot{x}_r \right) = -K_2 e_2 $$

由此可以解得控制律为

$$ \begin{aligned} u &= -ax^2 + \ddot{x}_r - e_1 -K_1 \left( v - \dot{x}_r \right) - K_2 e_2 \\ &= -ax^2 + \ddot{x}_r - \left( x-x_r \right) -K_1 \left( v - \dot{x}_r \right) - K_2 \left( v - \dot{x}_r + K_1 \left( x - x_r \right) \right) \\ &= -ax^2 + \ddot{x}_r - G_1 \left( x-x_r \right) - G_2 \left( v-\dot{x}_r \right) \end{aligned} $$

其中 $G_1 = 1 + K_1K_2,, G_2 = K_1 + K_2$ 将控制律写成了一般形式的状态（误差）反馈。非线性控制律由三部分构成：

• 非线性动态：利用 $-ax^2$ 将模型中的非线性偶和扣除，从而达到将模型线性化的目的，是反馈显性化的重要组成；
• 参考指令：$\ddot{x}_r$ 实际上是“开环控制”的指令，作为先验知识驱动被控对象跟随参考信号；
• 误差反馈：将状态与参考信号的误差进行反馈，是误差环路稳定的基本要素，可以通过调整控制参数调节误差的收敛动态。

最后，将误差的动态重新整理，可得

$$ \left\{ \begin{aligned} \dot{e}_1 & = -K_1e_1 + e_2 \\ \dot{e}_2 & = -e_1 - K_2e_2 \end{aligned} \right. $$

可见，非线性被控对象通过反馈，使得误差的动态为线性模型，称之为反馈线性化。误差动态的极点由以下方程给出

$$ \begin{vmatrix} -K_1-\lambda & 1 \\ -1 & -K_2-\lambda \end{vmatrix} = \lambda^2 + \left( K_1+K_2 \right) \lambda + K_1K_2+1 = 0 $$

设极点配置为 $p_1,,p_2$，相应的特征方程为

$$ \left( \lambda - p_1 \right) \left( \lambda - p_2 \right) = \lambda^2 - \left( p_1 + p_2 \right) \lambda + p_1 p_2 = 0 $$

对比以上两个式子可得

$$ \left\{ \begin{aligned} & K_1 + K_2 = - \left( p_1 + p_2 \right) \\ & K_1K_2 +1 = p_1p_2 \end{aligned} \right. \quad \Rightarrow \quad K_{1,2} = \frac{-\left( p_1+p_2 \right)\pm\sqrt{\left( p_1 - p_2 \right)^2+4}}{2} $$

仿真建模与验证

利用 Simulink 可以很容易验证上面的设计结果，仿真模型如下图所示：

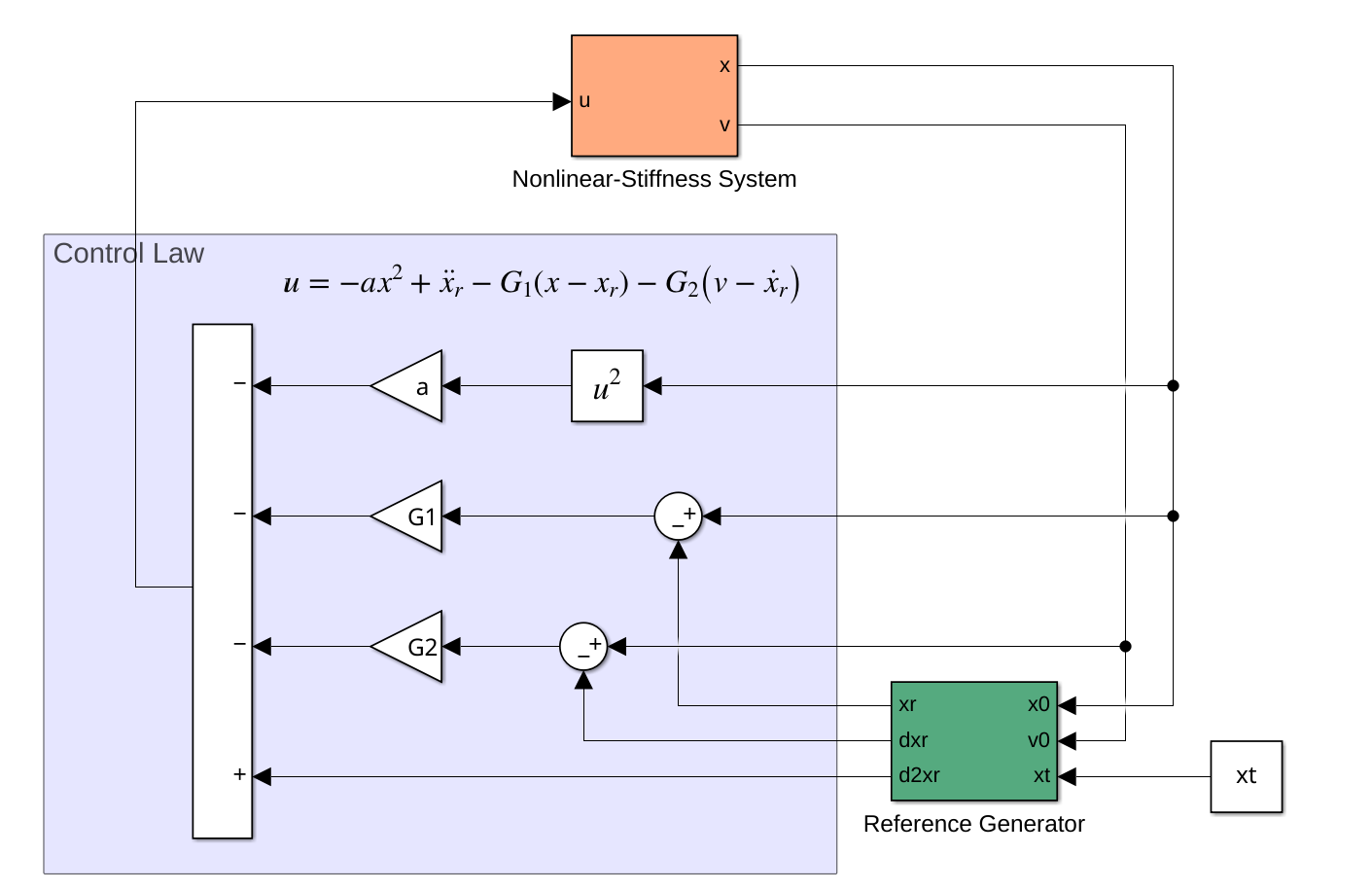
为了验证控制律，假设系统是理想的，即没有外部扰动和测量噪声、所有状态都精确可知。在实际情况下应当引入相应的噪声模型，并通过状态估计器对状态进行估计。

假设被控对象的初始位置与目标位置不同，利用该控制器将其控制到目标位置。在本例中，参考发生器使用三阶砰砰控制以对参考信号进行的微分，以使过渡过程光滑无超调。最终被控对象的位移响应如下图所示：

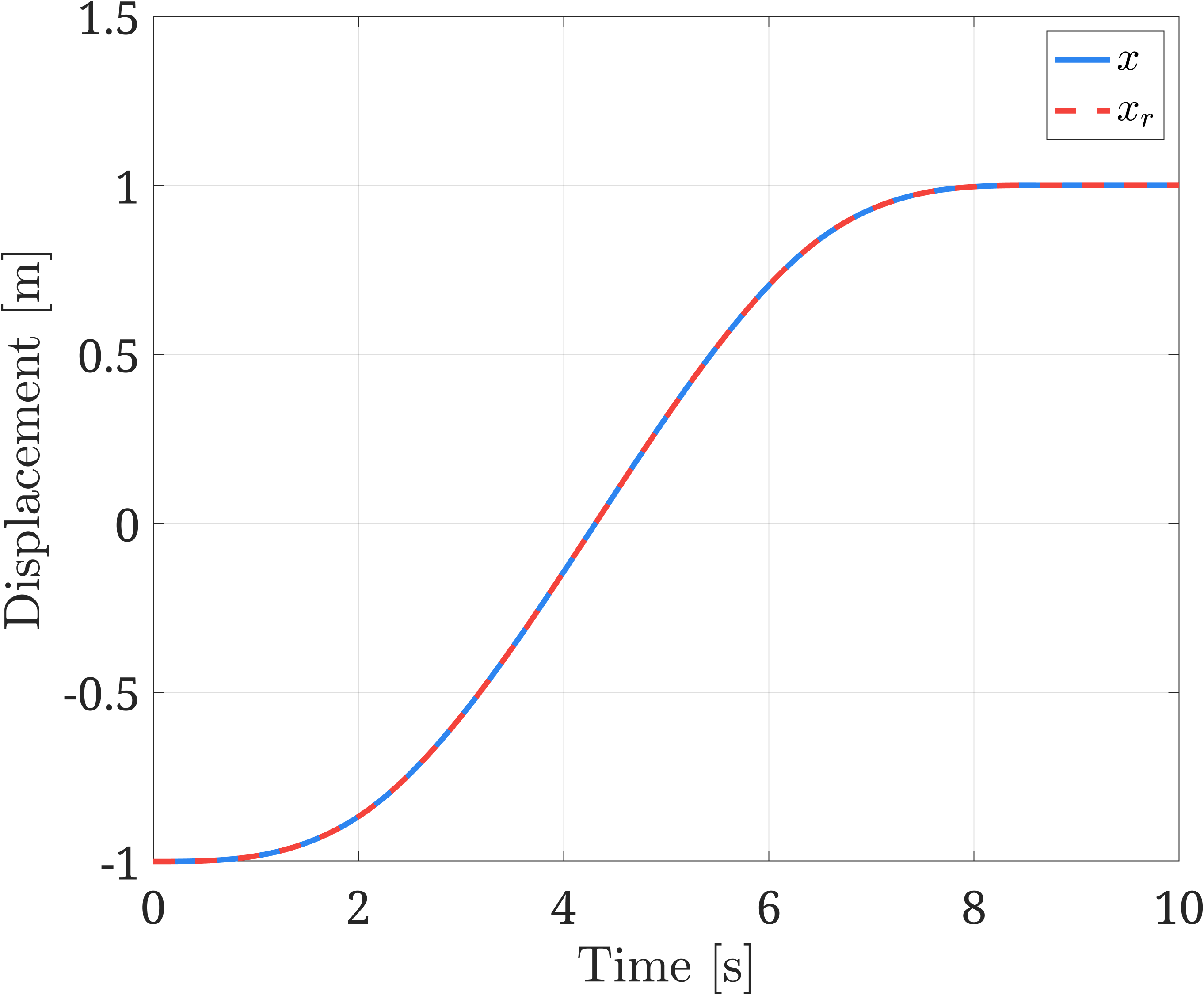
上述仿真模型我分享在了 GitHub 仓库，欢迎克隆、讨论、分享。

参考文献

1. DR_CAN, Nonlinear Backstepping Control.