航天器姿态测量与确定
航天器的姿态在变轨、通讯、充电等阶段起着十分重要的作用。姿态控制系统由传感器、姿态确定算法和控制律构成。本文将首先介绍几种常用姿态传感器的基本原理,然后对常用的定姿算法进行简要推导。
姿态测量
姿态传感器用于测量航天器当前姿态与参考方向之间的夹角,根据星表等信息获得参考方向在惯性系下的坐标,进一步可以确定航天器在惯性系下的姿态。对于航天器,常用的姿态传感器有地球敏感器、太阳敏感期、星敏感器等。
地球敏感器
对于近地轨道的卫星,地球的视角最大,立体角达到约 3.9 sr,因此不能使用点光源近似。地球敏感器旨在对地球的地平线进行测量,也称为地平仪(Horizon Sensor)。由于可见光范围内的地平线受到海洋、植物、沙漠等环境的影响,其表面并不均匀,而二氧化碳散发的 14.0 ~ 16.3 μm 范围的红外线更加均匀,所以大部分地平仪均对波长范围的红外线进行探测。
根据地球敏感器是否能够进行动态测量,可以将其分为辐射平衡式、圆锥扫描式、摆动扫描式三种类型。核心原理是测量地球四个边缘点相对于参考像点的位移,如下图所示。
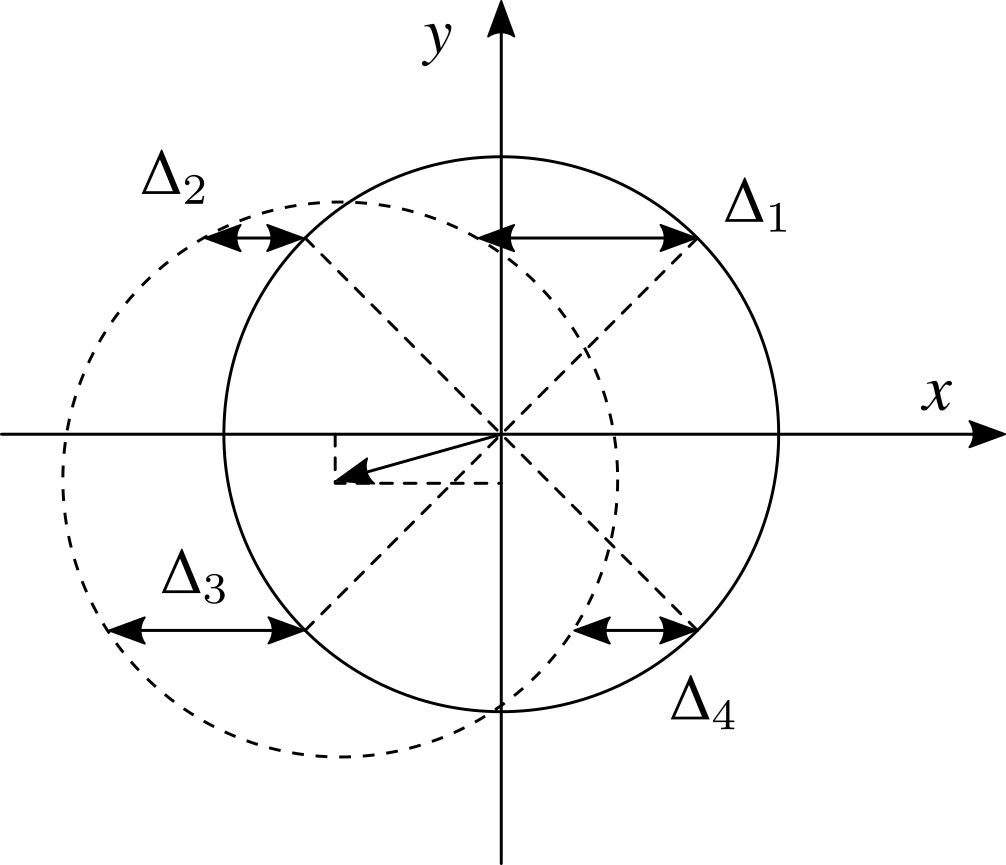
当航天器姿态相对地平面存在误差时,利用参考点的位移可以计算圆心的偏移,进而获得翻滚角和俯仰角。
太阳敏感器
太阳敏感器可分为模拟太阳敏感器和数字太阳敏感器,其中模拟太阳敏感器的基本元件为光电池,其输出电流与太阳光的入射角余弦成正比,常称为余弦传感器,基本方程为:
$$ I(\alpha) = I_0 \cos \alpha $$由于余弦函数在零位附近的斜率趋近于零,对微小角度的变化不敏感。为此,可以使用一对光电池对称分布于瞄准方向进行差分测量,如下图所示。
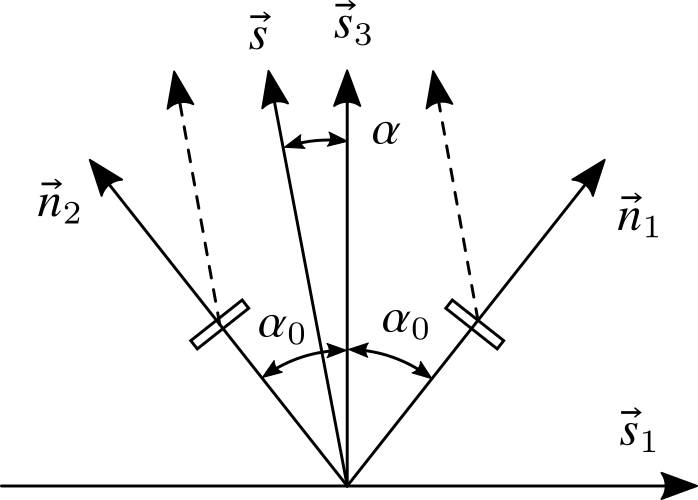
在这种布局下,两个光电池电流信号的差为:
$$ \Delta I (\alpha) = I_0 \cos \left( \alpha_0 - \alpha \right) - I_0 \cos \left( \alpha_0 + \alpha \right) = 2I_0 \sin\alpha_0 \sin \alpha $$此时传感器在零位附近具有 $2I_0\sin\alpha_0$ 的斜率,提高了小角度检测的灵敏度。
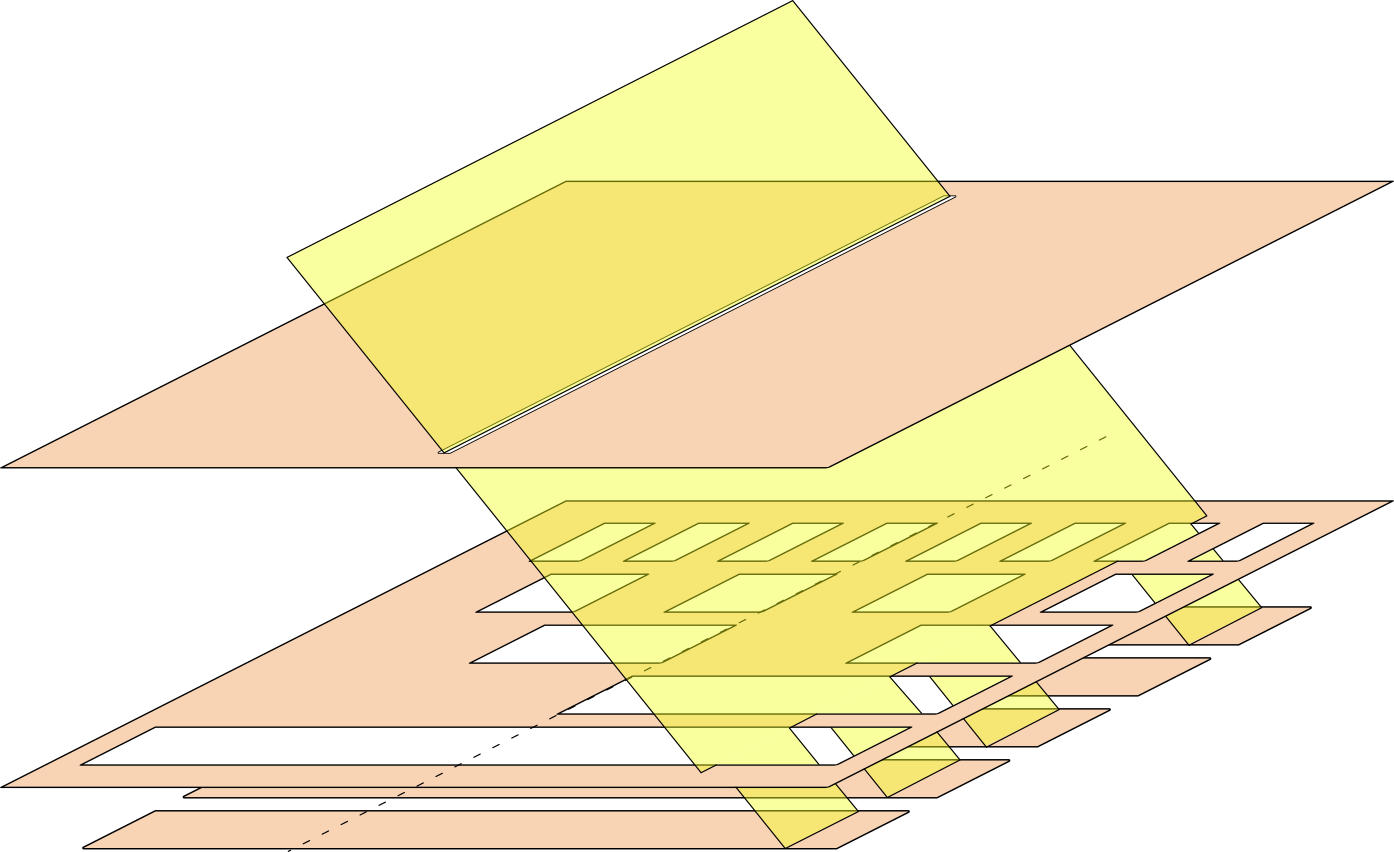
上图给出了数字太阳敏感器示意图:太阳光线首先通过顶层的狭缝变成线光源,以进行单方向入射角的测量。中间层具有不同尺寸的孔位用于编码(Gray Code),底层则是多个光电池用于检测太阳光是否透过编码孔位。由于光电池与入射角的余弦成正比,编码时的阈值会随之变动。因此,图中中间层最外侧的空隙允许所有视场(FoV:Field of View)内的光线透过,其下方光电池的电流作为阈值,作为其他光电池是否接收到光照的判据。第二个空隙为符号位,用于判断太阳光的入射方向;结合其他空隙的编码,可以将入射角进行量化,量化误差 $\rho_s$ 与位数 $\mu_s$ 的关系为:
$$ \rho_s = \frac{\alpha_\mathrm{max}}{2^{\mu_s-1}} $$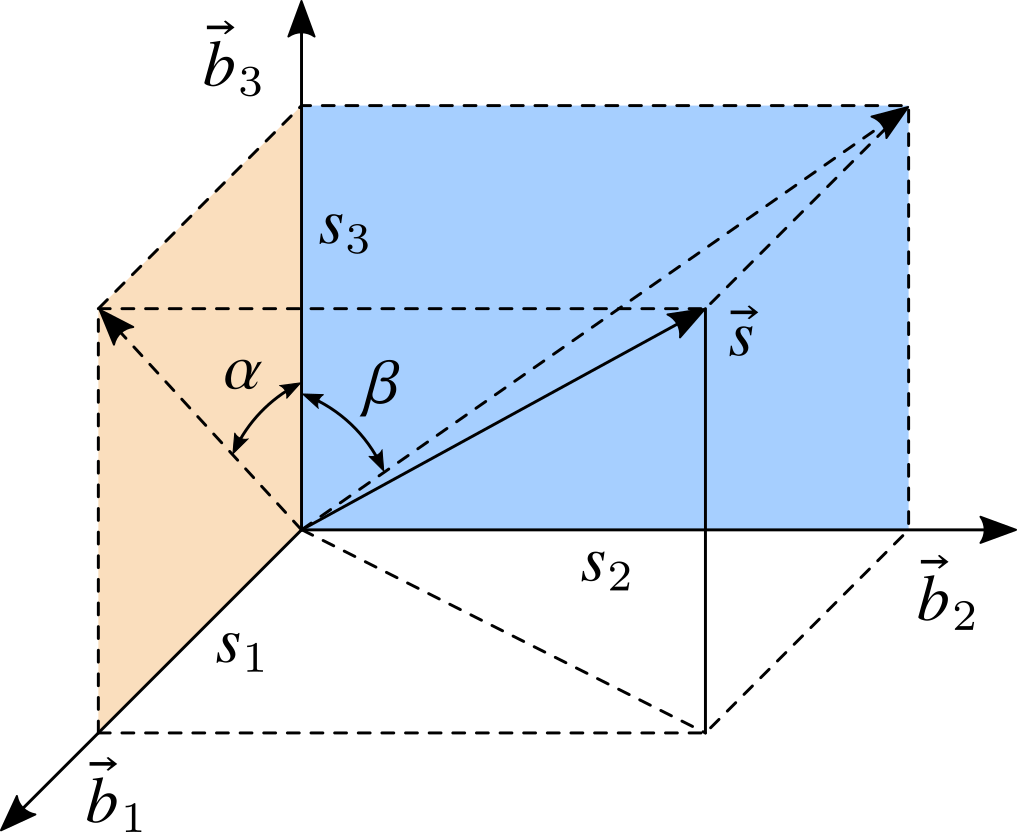
使用两个正交布置的单自由度太阳敏感器可以分别获得太阳方向在两个测量平面内投影与瞄准方向的夹角。设太阳敏感器测量坐标系与本体系相同,如上图所示。本体系下太阳的方向坐标记为 $\mathbf{s}^b = [s_1,,s_2,,s_3]^\mathrm{T}$,可以根据测得的夹角 $\alpha$ 和 $\beta$ 按下式计算:
$$ \mathbf{s}^b = \begin{bmatrix} s_1 \\ s_2 \\ s_3\end{bmatrix} = \frac{1}{\sqrt{ 1 + \tan^2 \alpha + \tan^2 \beta}} \begin{bmatrix} \tan\alpha \\ \tan\beta \\ 1 \end{bmatrix} $$星敏感器
星敏感器本质为数码相机,基本结构如下图所示。恒星发出的光线经过透镜汇聚与焦平面,焦平面由电荷耦合元件(CCD:Charge-Coupled Device)或者互补金属氧化物半导体(CMOS:Complementary Metal-Oxide Semiconductor)构成像素点对平面坐标进行量化。其中,CCD 具有更低的噪声,但更容易受到辐射的破坏;COMS 更能够抵抗环境的不利影响,且具有更大的视场。 CMOS 的技术与微处理器的技术相同,因此像素点兼具数据处理功能,称为有源像素传感器(APS:Active Pixel Sensor)。
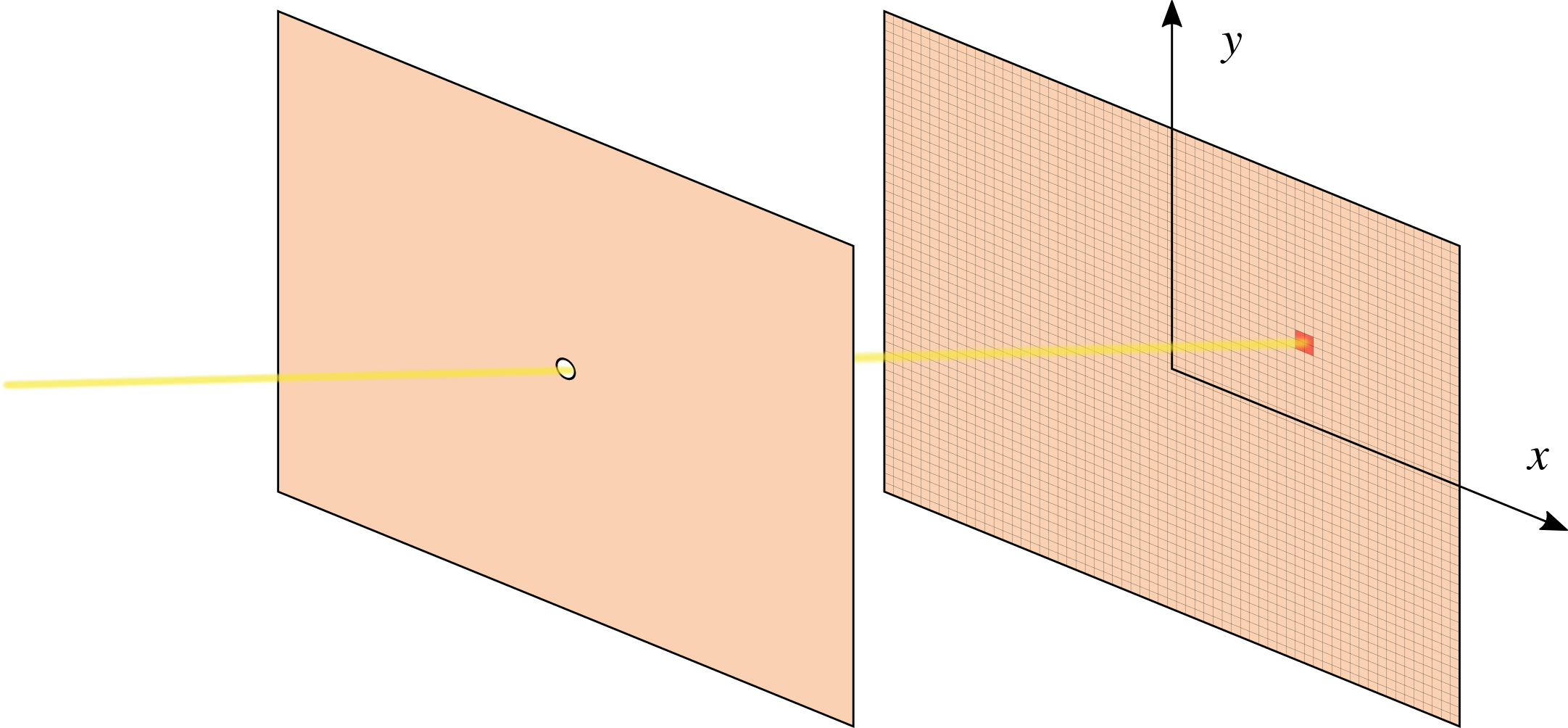
不同于地球敏感器和太阳敏感器具有特定的参考对象,星敏感器能够针对亮度达到一定阈值的许多恒星同时进行探测。因此,为了确定航天器的姿态,还需要对恒星进行识别,这使得星敏感器的数据处理依赖于复杂的匹配算法。星敏感器的数据刷新率一般在 0.5 Hz 到 10 Hz 之间。根据星敏感器是否对准已知恒星,可以分为两种工作模式:
- 初始姿态对准模式:该模式也被称为空间迷失模式(lost-in-space mode)。在这种情况下,星敏感器需要扫描整个视场,寻找最亮的像素簇,并至少计算三个簇的中心位置。根据间距、亮度以及其他特性在星表中搜索目标恒星。这个过程可以在数秒内完成;
- 跟踪模式:在星敏感器识别了特定的恒星后,航天器的姿态可以确定。相比于初始姿态对准模式,由于提前知道了航天器的姿态,在进行星表匹配时会简单很多。
星敏感器受到多种噪声的影响:其中光学失真可以通过标定进行校准;温度效应则可以通过温控将其影响最小化。除此之外,星敏感器还会受到散粒噪声的影响,可以通过增大望远镜孔径或延长积分时间来减小其影响。在没有光照时,暗电流也会引入误差,但可以通过对焦平面降温进行抑制;必要情况下,星敏感器的算法需要考虑暗电流引起的热像素的影响,将其在数据处理中予以扣除;另一方面,在确定姿态时,星表的误差也是姿态误差的一个来源,其中包括:恒星自身的微小运动、航天器位置引入的视差和恒星像差。下表给出了部分科学任务卫星的星敏感器性能对比:
| 任务 | 时间 | 视场 [°] | 精度(P/Y,R)["] | 刷新率 [Hz] |
|---|---|---|---|---|
| GRACE | 2002 | [±7, ±9.5] | [2.1, 16.5] | 1 |
| LISA Pathfinder | 2015 | 22 | [<1, <5] | 2 |
| GRACE-FO | 2018 | [±18, ±16] | [2.8, 23.7] | 2 |
姿态确定
姿态传感器给出了参考方向与传感器瞄准方向之间的夹角,结合传感器的安装信息,可以获得参考方向在航天器本体系下的坐标表示。为了进一步确定航天器的姿态,需要通过星表获得参考方向在惯性系下的坐标表示,并使用姿态确定算法计算姿态矩阵或四元数。本节简要介绍几种常用的定姿算法。
TRIAD 算法
TRIAD 算法(TRIaxial Attitude Determination)是最早发表的定姿算法,只需要对两个方向进行测量。其核心思想是根据两个参考矢量方向构造 TRIAD 坐标系,分别通过姿态传感器确定 TRIAD 坐标系与航天器本体坐标系的关系以及通过星表确定 TRIAD 坐标系与惯性系的关系,最后利用姿态矩阵的性质计算航天器的姿态。
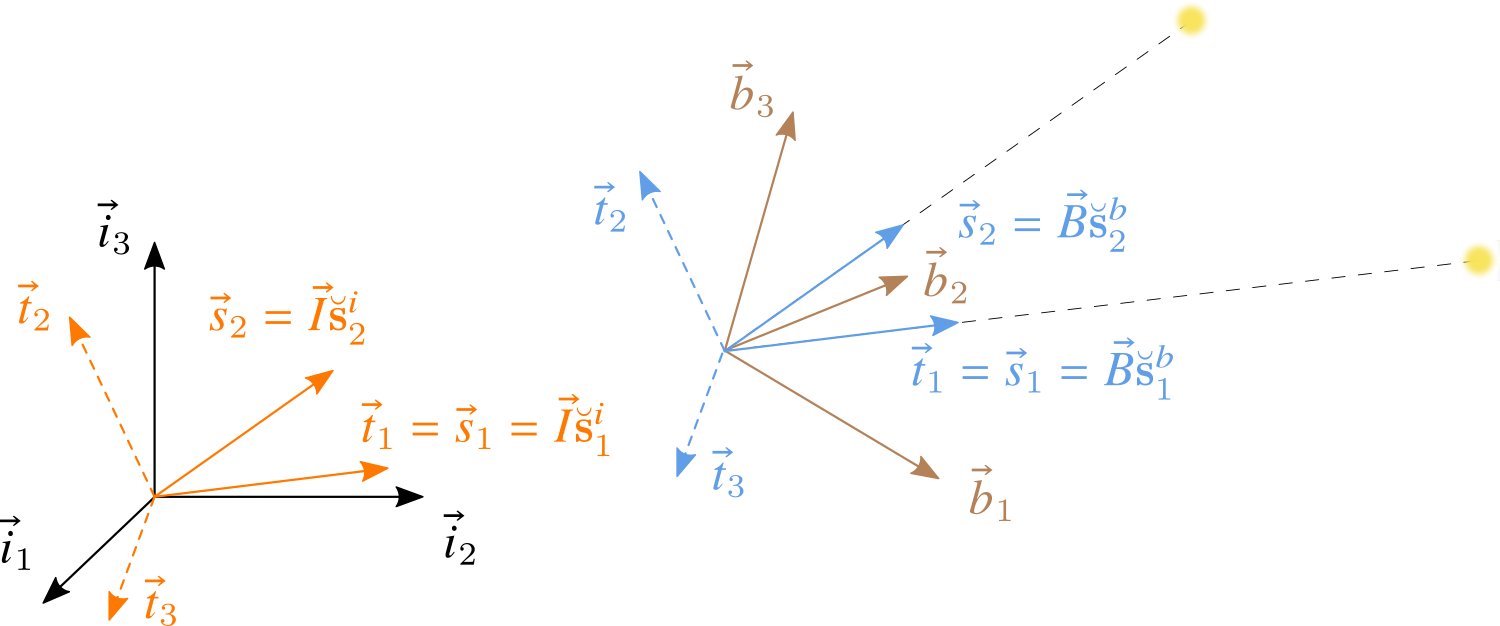
如上图所示,将航天器到远方恒星的单位矢量分别记做 $\vec{s}_1$ 和 $\vec{s}_2$,则 TRIAD 坐标系定义为:
$$ \vec{t}_1 = \vec{s}_1 ,\quad \vec{t}_2 = \frac{\vec{s}_1 \times \vec{s}_2}{\left\|\vec{s}_1 \times \vec{s}_2\right\|} ,\quad \vec{t}_3 = \vec{t}_1 \times \vec{t}_2 $$利用星敏感器可以计算恒星方向在本体参考系下的坐标 $\mathbf{s}_1^b$ 和 $\mathbf{s}_2^b$,因此 TRIAD 与本体系之间的坐标变换矩阵为:
$$ R_t^b = \begin{bmatrix} \mathbf{t}_1^b & \mathbf{t}_2^b & \mathbf{t}_3^b \end{bmatrix} $$同理,利用星表获得恒星方向在惯性系下的坐标,进而可以获得 TRIAD 与惯性系之间的关系:
$$ R_t^i = \begin{bmatrix} \mathbf{t}_1^i & \mathbf{t}_2^i & \mathbf{t}_3^i \end{bmatrix} $$因此航天器的姿态矩阵为:
$$ R_s^i =R_t^i R_b^t = R_t^i \left( R_t^b \right)^\mathrm{T} $$QUEST 算法
当可测的方向多于两个,且测量精度不同时,TRIAD 算法的使用将受到限制。这时的定姿问题可以转化为最优化问题:即寻找姿态矩阵 $R = R_b^i$ 使得误差的平方加权和最小,用数学表述为:
$$ \mathop{\arg\min}_R J(R),\quad J(R) = \frac{1}{2} \sum_{j=1}^m w_j \left\| \breve{\mathbf{s}}_j^b - R^\mathrm{T}\breve{\mathbf{s}}_j^i \right\|^2 $$这个问题被称为 Wahba 问题,其中 $w_j$ 为权值,一般有:
$$ \sum_{j=1}^m w_j = w_0 = 1 $$考察优化目标函数:
$$ \begin{aligned} J(R) &= \frac{1}{2} \sum_{j=1}^m w_j \left( \breve{\mathbf{s}}_j^b - R^\mathrm{T}\breve{\mathbf{s}}_j^i \right)^\mathrm{T} \left( \breve{\mathbf{s}}_j^b - R^\mathrm{T}\breve{\mathbf{s}}_j^i \right) \\ &= \frac{1}{2} \sum_{j=1}^m \left(2 - 2 \bigl(\breve{\mathbf{s}}_j^i \bigr)^\mathrm{T} R \breve{\mathbf{s}}_j^b\right) \\ &= w_0 - \sum_{j=1}^m \bigl(\breve{\mathbf{s}}_j^i \bigr)^\mathrm{T} R \breve{\mathbf{s}}_j^b \\ &= w_0 - \sum_{j=1}^m \mathrm{tr} \left( w_j \breve{\mathbf{s}}_j^b \bigl( R^\mathrm{T} \breve{\mathbf{s}}_j^i \bigr)^\mathrm{T} \right) \\ &= w_0 - \mathrm{tr} \left( \sum_{j=1}^m \left( w_j \breve{\mathbf{s}}_j^b \bigl(\breve{\mathbf{s}}_j^i \bigr)^\mathrm{T} \right) R \right) \end{aligned} $$定义矩阵 $W$ 为:
$$ W = \sum_{j=1}^m \left( w_j \breve{\mathbf{s}}_j^b \bigl(\breve{\mathbf{s}}_j^i \bigr)^\mathrm{T} \right) $$原优化目标可转化为:
$$ \mathop{\arg\min}_R J(R) \quad \rightarrow \quad \mathop{\arg\max}_R \mathrm{tr}\bigl( WR \bigr) = \mathop{\arg\max}_R \mathrm{tr}\bigl( RW \bigr) $$姿态矩阵 $R$ 有 $9$ 个参数,但只有 $3$ 个自由度,为了便于数值计算,矩阵表述转化为四元数 $\mathfrak{q} = \mathfrak{q}_s^i = [q_0,\,q_1,\,q_2,\,q_3]^\mathrm{T}$,上式可化为:
$$ \begin{aligned} \mathrm{tr}\bigl( RW \bigr) &= \mathrm{tr}\Bigl( \bigl(2 \mathbf{q} \mathbf{q}^\mathrm{T} + (q_0^2 - \mathbf{q}^\mathrm{T} \mathbf{q})I + 2q_0 \mathbf{q} \times \bigr) W \Bigr) \\ &= \mathfrak{q}^\mathrm{T} \begin{bmatrix} w & \mathbf{w}^\mathrm{T} \\ \mathbf{w} & W + W^\mathrm{T} - wI \end{bmatrix} \mathfrak{q} \end{aligned} $$其中:
$$ w = \mathrm{tr}(W),\quad \mathbf{w} = \sum_{j=1}^m w_j \breve{\mathbf{s}}_j^b \times \breve{\mathbf{s}}_j^i ,\quad Q = \begin{bmatrix} w & \mathbf{w}^\mathrm{T} \\ \mathbf{w} & W + W^\mathrm{T} - wI \end{bmatrix} $$在四元数表述下,Wahba 问题变为有约束条件下的极值问题:
$$ \mathop{\arg\max}_\mathfrak{q} \mathfrak{q}^\mathrm{T} Q \mathfrak{q} ,\quad \mathfrak{q}^\mathrm{T} \mathfrak{q} = 1 $$这类问题可以利用拉格朗日乘数法进行求解,记:
$$ L(\mathfrak{q},\,\lambda) = \frac{1}{2} \mathfrak{q}^\mathrm{T} Q \mathfrak{q} + \lambda \bigl( 1 - \mathfrak{q}^\mathrm{T} \mathfrak{q} \bigr) $$则优化问题的解由下述方程组给出:
$$ \left\{ \begin{aligned} \frac{\partial L}{\mathfrak{q}} &= (Q-\lambda I) \mathfrak{q} = 0 \\ \frac{\partial L}{\lambda} &= 1 - \mathfrak{q}^\mathrm{T} \mathfrak{q} = 0 \end{aligned} \right. $$进一步分析可知,最优四元数为矩阵 $Q$ 最大特征值对应的特征向量。因此姿态四元数的获取可以依据矩阵的特征值分解得到,这种方法称为 Q 方法(Q-Method)。
由于最优解只与 $Q$ 矩阵的最大特征值相关,分解全部特征值会增加不必要的计算量。QUEST 算法利用解的特性避免了特征值分解,其基本思想为:构造 $Q$ 矩阵后计算其特征多项式,取初值 $\hat{\lambda}_{\mathrm{max},0} = w_0 = 1$ 进行牛顿迭代计算最大特征值,利用 $(Q-\hat{\lambda}_\mathrm{max} I) \mathfrak{q} = 0$ 求解四元数。更进一步地,使用吉布斯参数 $\mathbf{p} = \mathbf{q}/q_0$ 可以简化计算,最后结果为:
$$ \begin{aligned} \mathbf{p} &= \Bigl( \bigl( \hat{\lambda}_\mathrm{max} + w\bigr)I - \bigl( W + W^\mathrm{T} \bigr) \Bigr)^{-1} \mathbf{w} \\ \hat{\mathfrak{q}} &= \frac{1}{\sqrt{1+\mathbf{p}^\mathrm{T}\mathbf{p}}} \begin{bmatrix} 1 \\ \mathbf{p} \end{bmatrix} \end{aligned} $$状态估计器
QUEST 算法允许将多个姿态传感器的数据进行融合,使用状态估计器可以进一步将不同类型传感器的数据进行融合,如融合陀螺仪和星敏感器的数据对姿态进行估计。状态估计器的基本思路如下图所示,针对航天器的运动学模型构造实时运行的数值模型,将测得的角速度输入给数值模型,利用姿态估计误差 $\tilde{\mathfrak{q}}=\hat{\mathfrak{q}}^{-1}\otimes \breve{\mathfrak{q}}$ 进行反馈,可以对状态进行修正。进一步,如果对扰动进行建模,还能够对陀螺仪的零偏进行修正,进一步提高姿态的估计精度。
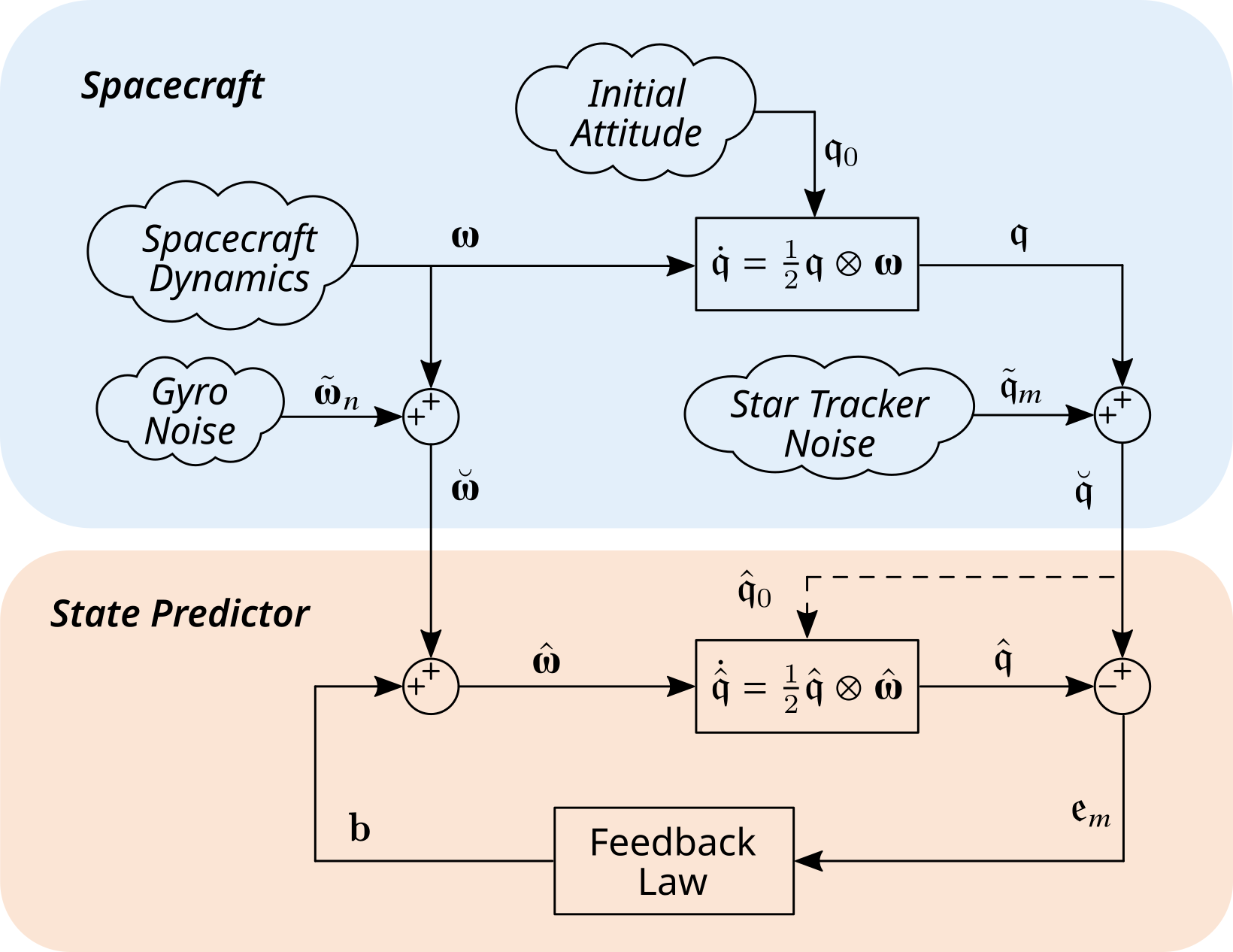
图中的反馈可以使用卡尔曼增益以获得最优估计,参考之前讨论的卡尔曼滤波简介。需要注意的是,由于姿态的运动学方程是非线性的,应当基于上一次的后验估计对模型进行线性化,构成扩展卡尔曼滤波器(EKF:Extended Kalman Filter)。对于频域设计而言,可以使用适当的极点配置设计环路的灵敏度函数,这一点我们将在以后的模型嵌入控制(EMC:Embedded Model Control)中进行详细讨论。
参考文献
- 吕振铎, 雷拥军. 卫星姿态测量与确定. 国防工业出版社. 2013.
- E. Canuto, C. Novara, D. Carlucci, et al. Spacecraft Dynamics and Control: The Embedded Model Control Approach. Butterworth-Heinemann. 2018.
- Spacecraft Sun Sensors. NASA Space Vehicle Design Criteria (Guidance and Control). 1970.
- F.L. Markley, J.L. Crassidis. Fundamentals of Spacecraft Attitude Determination and Control. Springer. 2014.
- C. Dunn, W. Bertiger, G. Franklin, et al. The Instrument on NASA’s GRACE Mission: Augmentation of GPS to Achieve Unprecedented Gravity Field Measurements. 15th International Technical Meeting of the Satellite Division of The Institute of Navigation. 2002.
- J. Herman, D. Presti, A. Codazzi, C. Belle. Attitude Control for GRACE the First Low-Flying Satellite Formation. 18th International Symposium on Space Flight Dynamics. 2004.
- L. Giulicchi, S.-F. Wu, T. Fenal. Attitude and orbit control systems for the LISA Pathfinder mission. Aerospace Science and Technology. 2013.
- LISA Pathfinder Spacecraft Overview.
- C.R. Patel. Analyzing and monitoring GRACE-FO star camera performance in a changing environment. The University of Texas at Austin. 2020.