A* 算法简介
A*(AStar)是一个兼具效率和效果的图搜索算法,可用于目标点之间的路径规划。本文将以广度优先搜索为基础,逐步介绍图搜索的基本方法,最后给出 A* 算法及其 MATLAB 实现示例。
路径规划的目标是在图中找到一条连续可达的状态集,使之按顺序由给定的起始状态达到目标状态。广义的 “图” 可以看作是状态转移的集合,即给定任意状态,只要能够给出下一个可行状态的集合,这种映射关系就能称为 “图”。最形象的图就是地图,以二维网格图为例,任意一个状态(位置),下一步可行的位置为当前位置的上、左、下、右四个方向(边界除外)。本文不打算对图进行过多讨论,后续算法也将以二维网格图为例进行介绍。
为了找到一条符合要求的路径,根本思路就是对图进行遍历。我们将循序渐进地讨论不同的遍历方式,最终看看 A* 如何以更加 “聪明” 的方法进行搜索。
广度优先搜索
想象一个迷宫的游戏,为了找到出口,我们可以任意选择一条可行的路,然后一路走下去,如果遇到死胡同,则回到最近的岔路口选择另一条可行的路继续尝试,直到到达出口为止。这种方法称为深度优先搜索(DFS,Depth First Search)。
然而,当可行的道路相对于死胡同数量更少时,过于深入地探索死胡同会降低效率。因此我们将倾向于“广撒网”式搜索,称之为广度优先搜索(BFS,Breadth First Search),其基本思路为:记录已经达到的位置和边界,依次从边界中挑出新的位置并探索其周边以对边界进行扩展,直到达到目标位置。这个过程可以形象地想象为气球的膨胀。更进一步,如果记录每个位置的上一个位置,只需要从终点开始依次读取上一个位置,就可以得到由终点到起点的路径,最后反序即可得到最终的路径了。
广度优先搜索可以用伪代码表示为:
初始化 Open Set 用于记录边界,并将起点放入 Open Set
初始化 Closed Set 用于记录已经到达的位置
当 Open Set 不为空时执行如下循环:
从 Open Set 中取出并删除第一个位置 current
将 current 放入到 Closed Set(表示已经搜索过这个点)
如果 current 为目标点:
提前终止循环
根据地图,查找 current 下一步可以到达的所有位置,记为 neighbors
对 neighbors 的每个元素进行如下操作:
记录其来源为 current(即可以从 current 达到 neighbors)
将其放到 Open Set 末尾(如果已经在里面则可以忽略或覆写)
(假设存在由起点到终点的路径,则循环停止时已经搜索到终点)
从终点开始,依次访问各个位置的来源,构成由终点到起点的路径
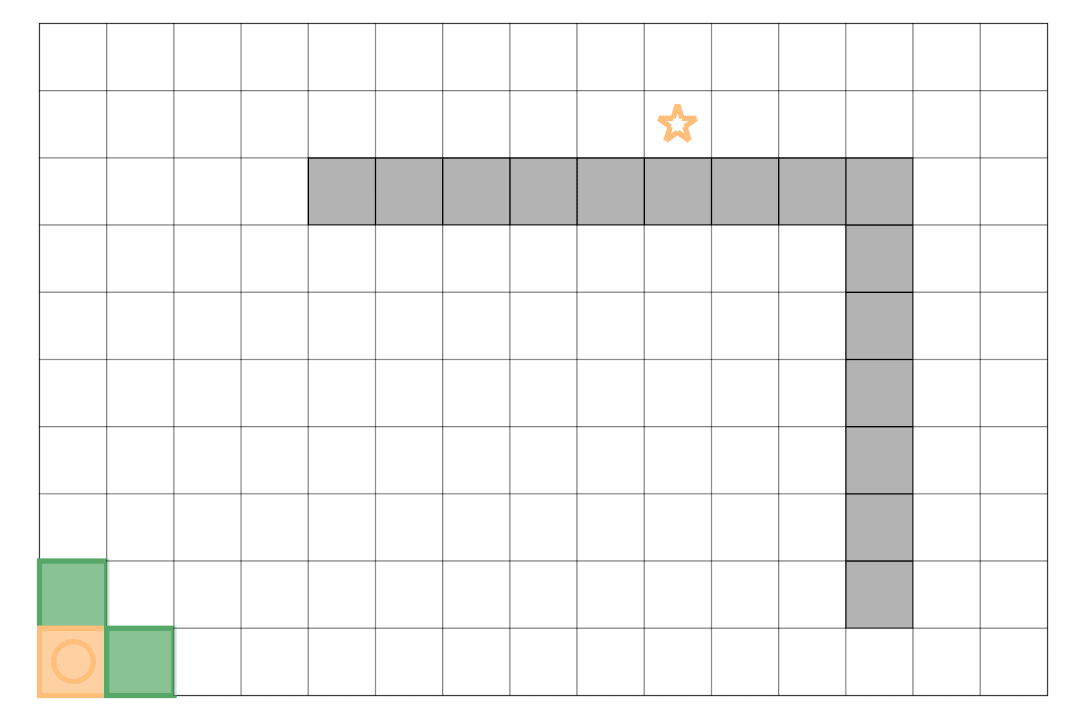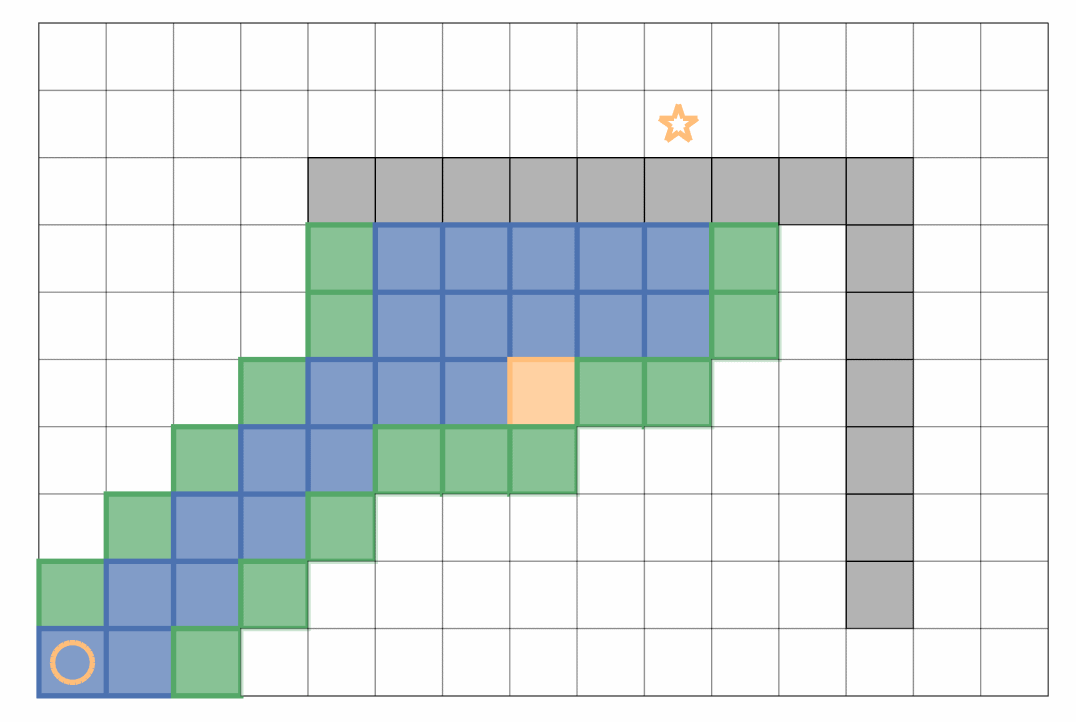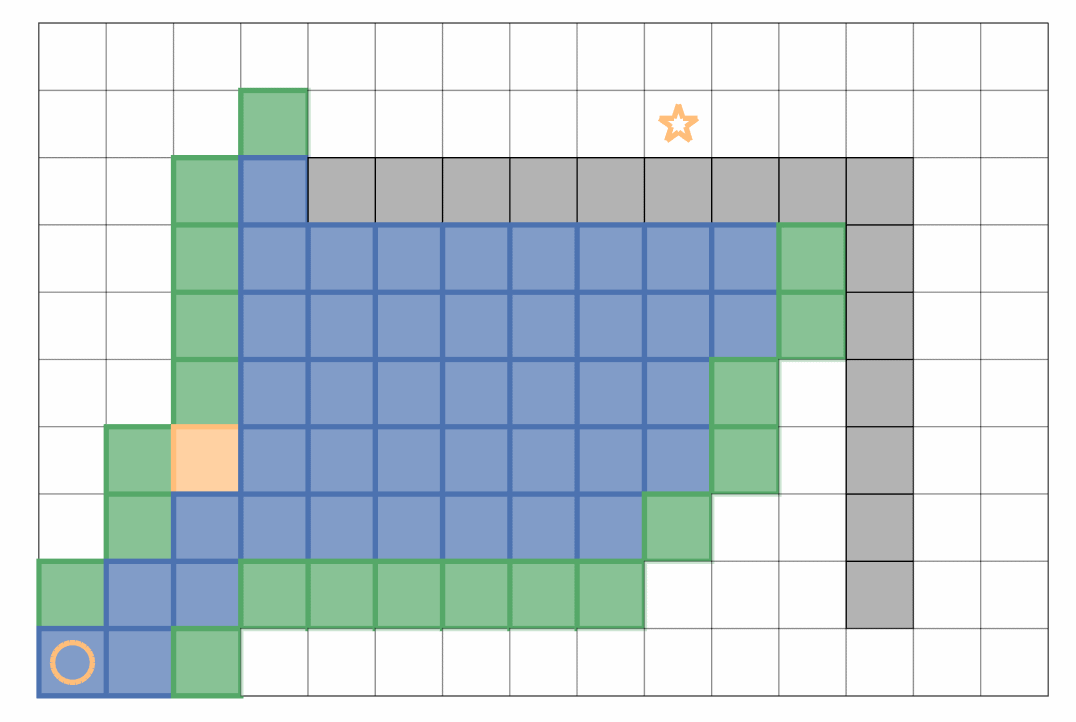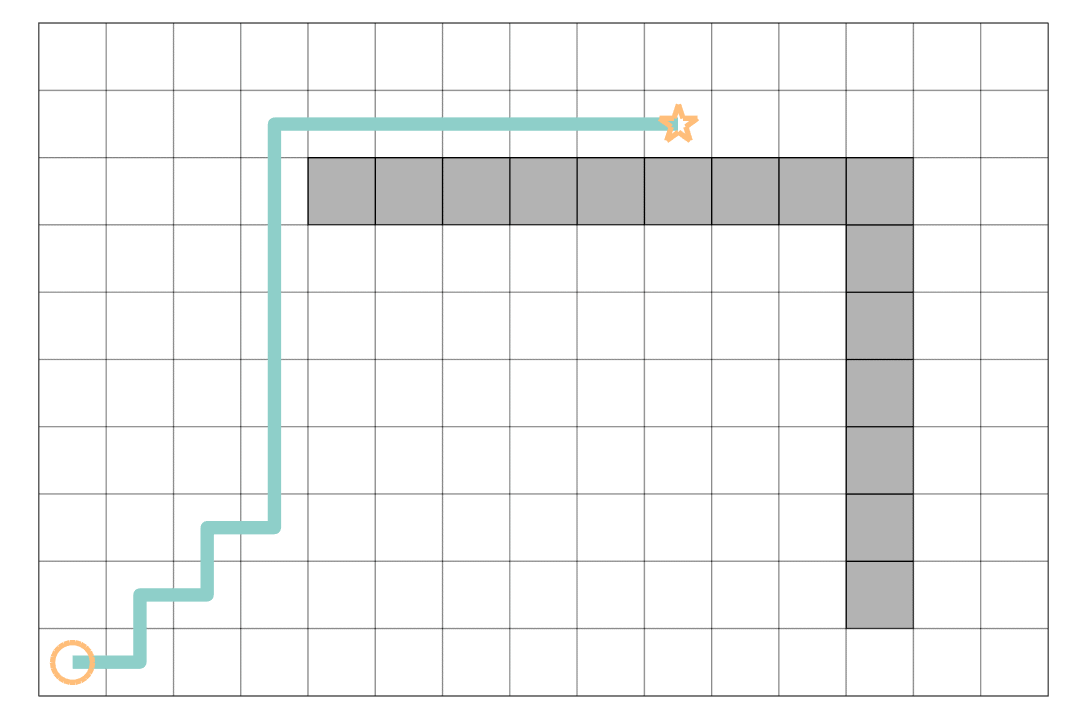
将上面的路径逆序排列,得到由起点到终点的路径广度优先搜索的示例如下:黄色圆圈表示起点,黄色五角星代表终点;黄色方块为当前弹出的位置,绿色方块为 Open Set 记录的边界,蓝色方块则是 Closed Set 中记录的已经搜索过的位置。
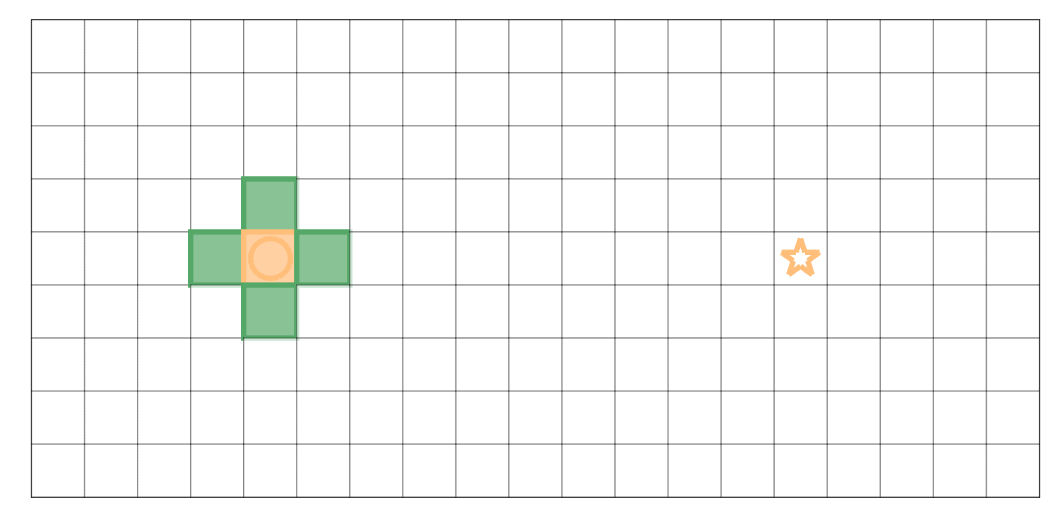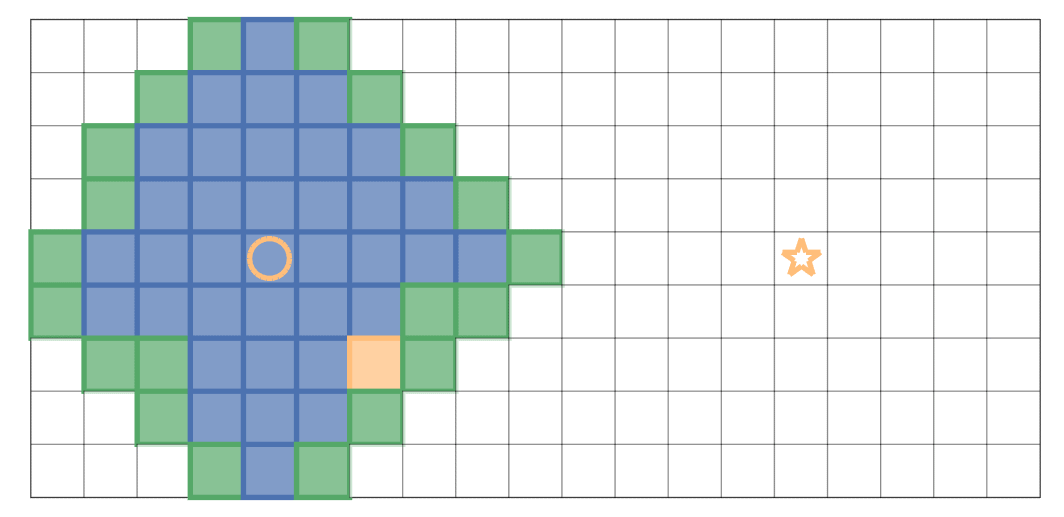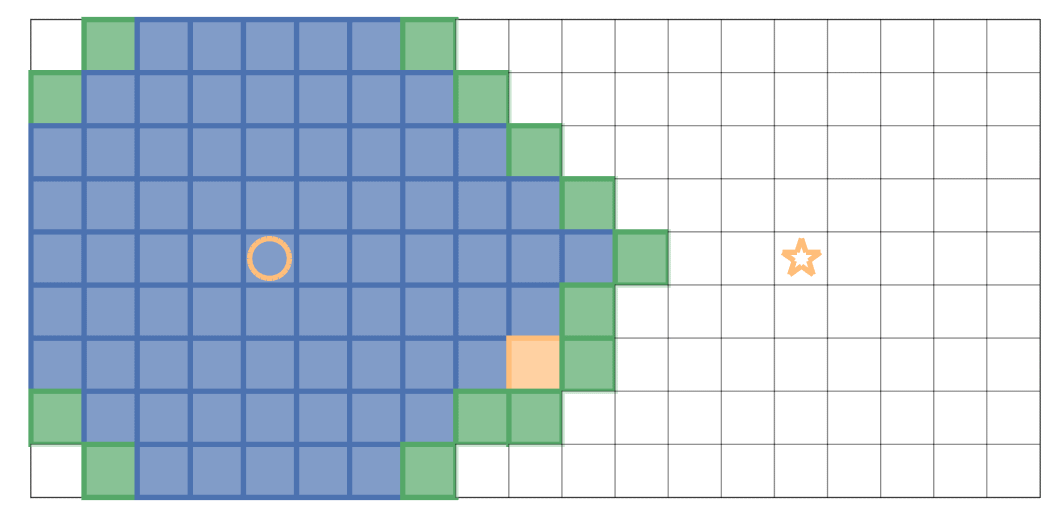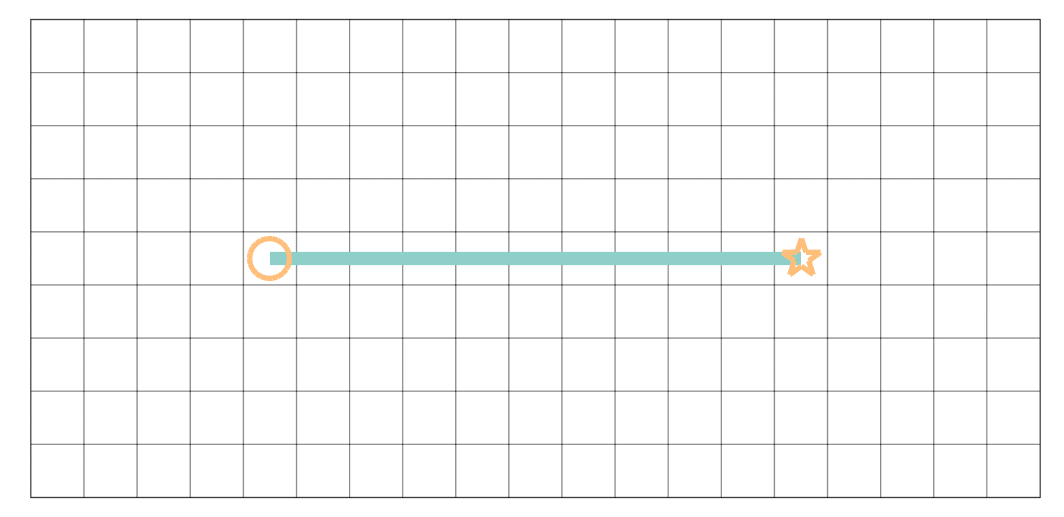
贪心算法
如上面的例子所示,广度优先搜索按照先入先出的顺序从 Open Set 弹出(取出并删除)一个待搜索的位置(后称之为节点),表现为均匀地向外搜索。考虑到在大多数情况下,向目标反方向搜索是不划算的。贪心算法(Greedy Best First Search)则希望利用终点的信息引导搜索方向。
引导搜索方向的本质是调整从 Open Set 中弹出节点的顺序,因此各个节点应当有 “优先级” 的区别。我们定义启发函数(Heuristic Function)为指定节点到目标点的距离,因此距离越近的点 “代价” 越低,优先级越高。
于是贪心算法对上述伪代码的第 5 行和第 14 行对 Open Set 的操作进行了改动:
- 第 5 行(如何弹出):弹出 Open Set 中优先级代价最小(优先级最高)的节点;
- 第 14 行(如何放入):将 neighbors 的元素放入 Open Set 时同时根据启发函数计算代价并一同计入,如果已经有该节点,则替换为代价更小的节点。
贪心算法在启发函数的引导下优先往目标点靠近搜索,然而当存在障碍物时,过于贪心容易错失最优路径,一个简单的例子如下:
Dijkstra 算法
如果说贪心算法解决的是理想情况下最高效的搜索方法,那么 Dijkstra 算法则注重最终结果的最优特性。我们重新考虑广度优先搜索的第 14 行:如果某个节点已经在 Open Set 中(意味着其来源为其他位置),广度优先搜索可以采用覆盖或忽略,并没有考虑不同来源的代价。
为此,Dijkstra 算法需要进一步知道每一步移动所需的代价(这可以由地图来决定),并记录从起点到每个到达节点的累计代价。当某个节点可以从不同方向达到时,需要选择累计代价最小的进行替换。因此广度优先搜索的第 14 行应当扩展为:
(对于 neighbors 中的某个节点)
计算从 current 过来的代价(current 的累计代价加上这一步移动的代价)
如果它已经存在 Closed Set:
如果从 current 过来的代价比 Closed Set 中记录的代价更低:
将该节点从 Closed Set 中删除
将该节点重新放入 Open Set,更新其父节点和累计代价(需要将其作为边界重新搜索,以更新其后节点的累计代价)
否则:
(什么也不做)
否则(不在 Open Set 中):
将该节点放入 Open Set,并记录其父节点和累计代价该算法的示例如下:在广度优先搜索 “广撒网” 的基础上,通过持续更新代价信息,最终可以得到代价最小的路径(本例没有定义拐弯的代价,因此存在多种折线的最优路径)。
A* 算法
讨论了贪心算法的启发函数和 Dijkstra 算法引入的 “实际代价” 的思想,两者结合即构成了 A* 算法:在将节点放入 Open Set 时,将累计代价和启发代价之和作为优先级存入;当 Open Set 已经存在节点时,只比较实际的累计代价来决定是否替换。如此做,启发代价只用于引导搜索方向,而实际代价决定了最终输出的最优路径。
使用 MATLAB 自编的 A* 算法分享在 GitHub 仓库 AStar-MATLAB,其核心代码如下:
% 采用函数句柄将启发函数设置为当前节点与目标节点的距离
heuristic = @(node) sqrt((goal.row - node.row)^2 + (goal.col - node.col)^2);
% 初始化
open = PriorityQueue; % 采用优先队列初始化 Open Set
open.push(start, 0); % 将起始点添加到 Open Set
closed = dictionary; % 使用 Hash 表初始化 Closed Set
while open.size > 0
current = open.pop; % 从 Open Set 中弹出优先级最高(代价最低)的节点
closed(current.key) = current; % 将当前节点放入 Closed Set,表示已经搜索过
if current == goal % 如果当前节点为目标节点,提前终止循环
goal = current; % 更新目标节点的父节点和累计代价信息
break
end
neighbors = map.neighbors(current); % 根据地图获取当前节点的周围节点(同时计算了累计代价)
for k = 1:length(neighbors)
key = neighbors(k).key;
% 根据累计代价和启发代价计算优先级
priority = neighbors(k).cost + heuristic(neighbors(k));
if isKey(closed, key)
% 如果 Closed Set 存在当前节点(已经搜索过),根据实际代价确定是否替换
if neighbors(k).cost < closed(key).cost
closed(key) = [];
open.push(neighbors(k), priority)
end
else
open.push(neighbors(k), priority)
end
end
% 从终点开始反向索引各节点的父节点并记录
node = goal;
astar_path = zeros(goal.depth, 3);
for k = 1:goal.depth
astar_path(k, :) = [node.row, node.col, node.cost];
node = node.parent;
end
% 逆序,获得从起点到终点的路径
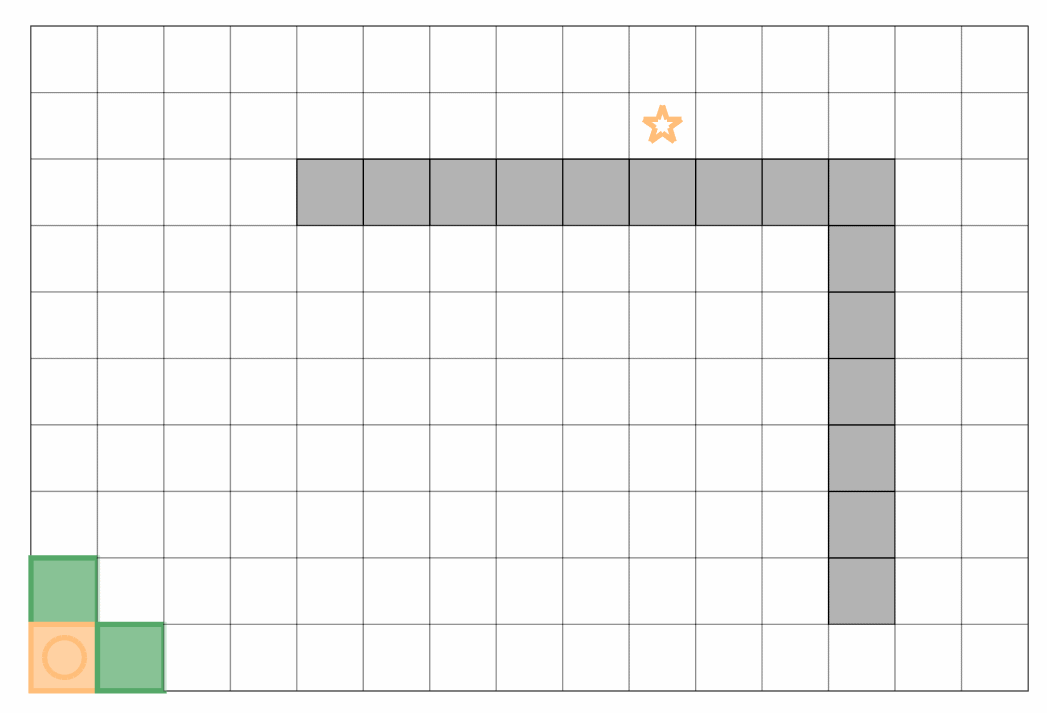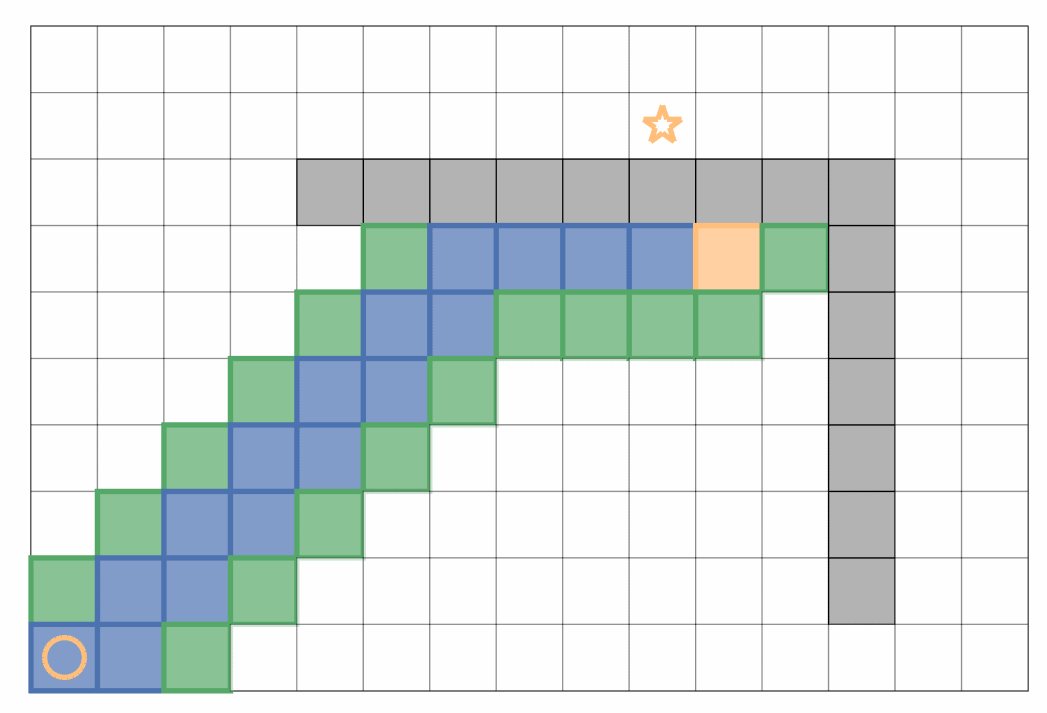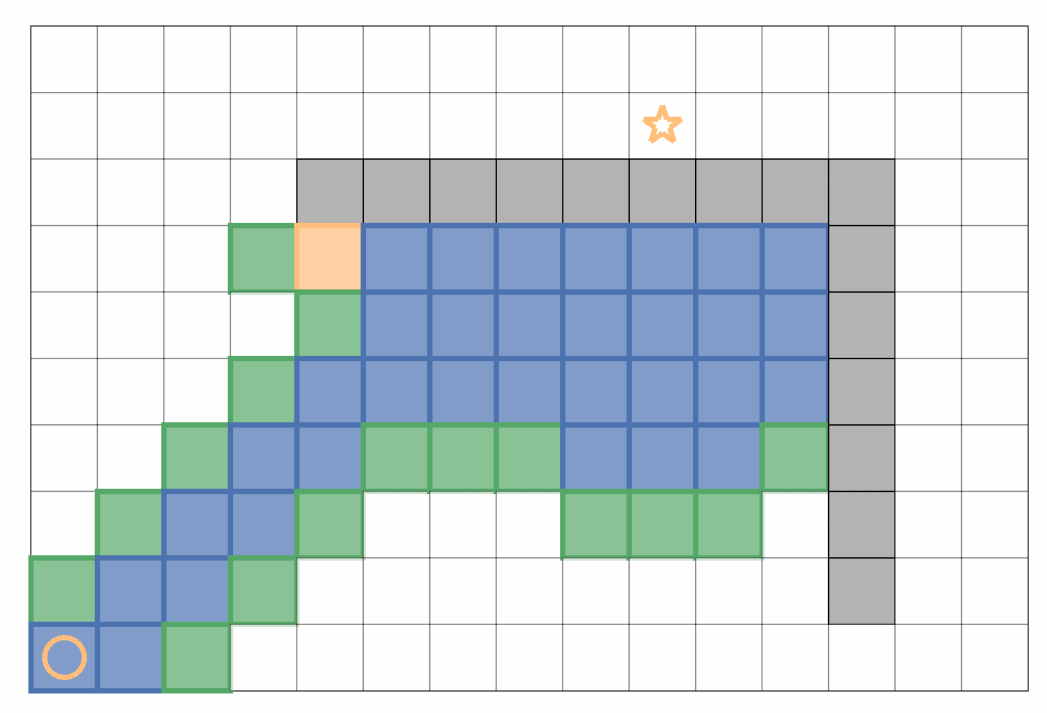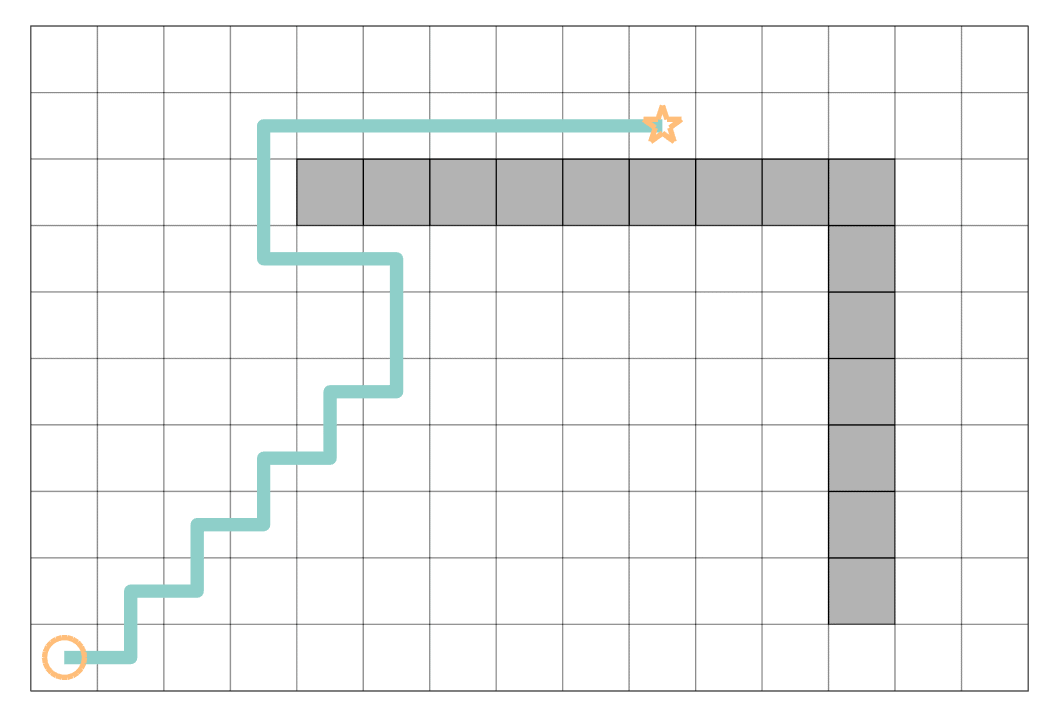
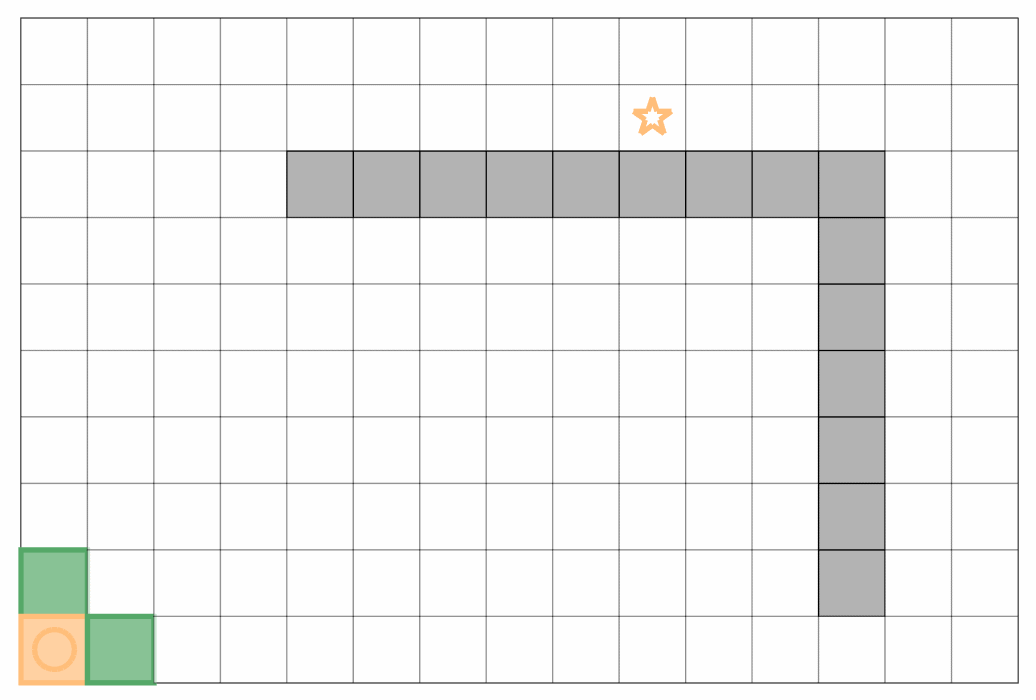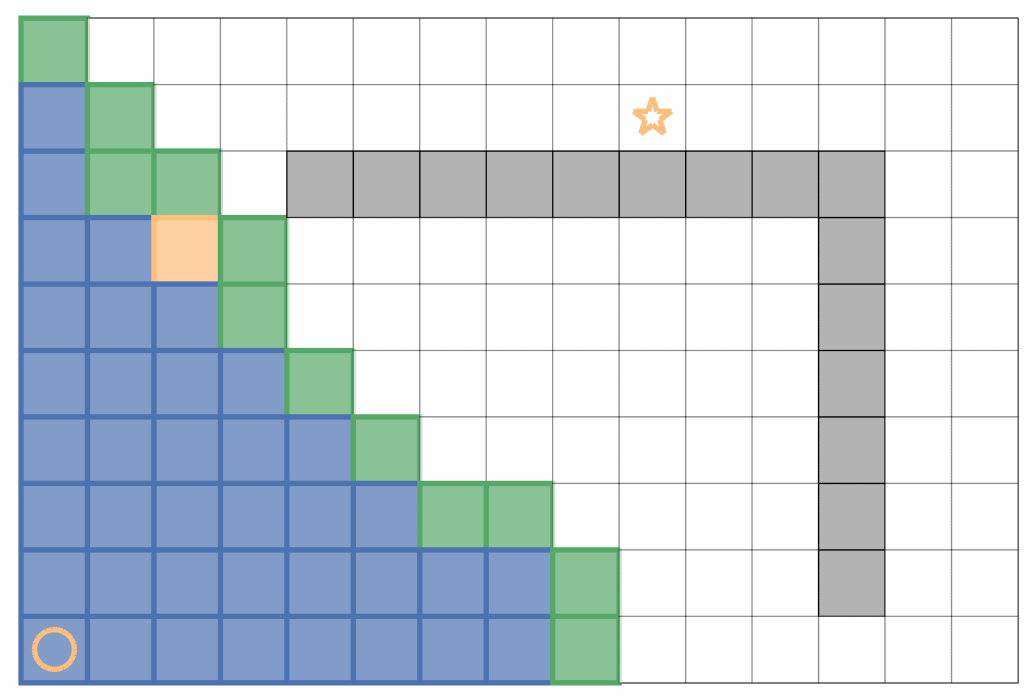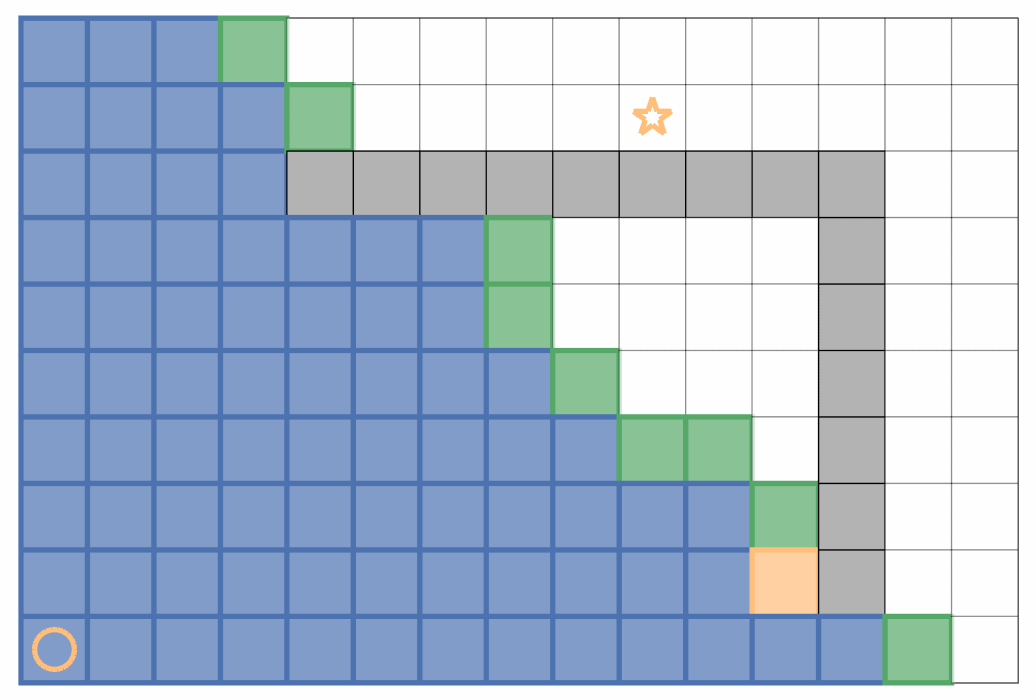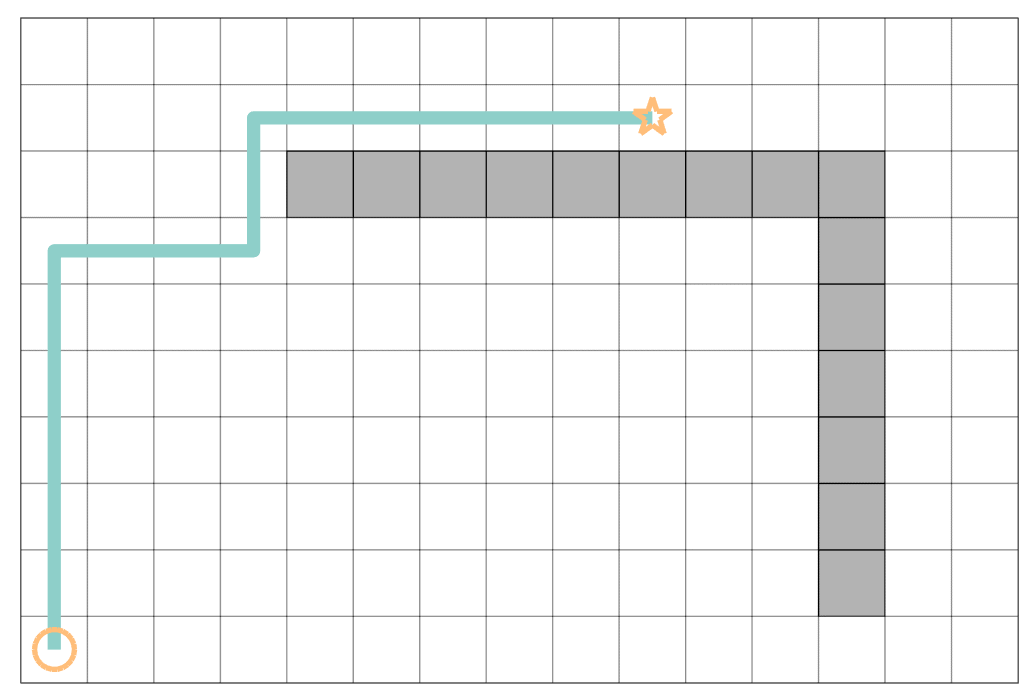
astar_path = astar_path(end:-1:1, :);最终基于 A* 的路径搜索示例如下:
参考文献
- Red Blob Games. Introduction to the A* Algorithm.
- Hart P. E., Nilsson N. J., Raphael B. A Formal Basis for the Heuristic Determination of Minimum Cost Paths. IEEE Transactions on Systems Science and Cybernetics 1968, 4(2), 100–107.
- ITCharge. 堆排序. 算法通关手册.
- ITCharge. 优先队列基础知识. 算法通关手册.